积分：数学未被遗忘的进化

2023-11-19 理论教育版权反馈

【摘要】：所谓“积分”，“积”是“积集，累积”的意思，“分”是“分割，细分”的意思，那么，“积分”的含义就是将某个东西先进行细分，然后再累加起来的一种计算方法.积分起源于求面积的计算.据记载，早在远古时期，尼罗河两岸的农田是按面积征税的，因此，当每年河水泛滥破坏了一部分土地后，农民会请求相应地减少税额，这时收税官就要确定究竟损失了多少土地，这就需要发明一些初等几何图形的面积计算技术.埃及人的面积计算方法的基

所谓“积分”，“积”是“积集，累积”的意思，“分”是“分割，细分”的意思，那么，“积分”的含义就是将某个东西先进行细分，然后再累加起来的一种计算方法.积分起源于求面积的计算.据记载，早在远古时期，尼罗河两岸的农田是按面积征税的，因此，当每年河水泛滥破坏了一部分土地后，农民会请求相应地减少税额，这时收税官就要确定究竟损失了多少土地，这就需要发明一些初等几何图形的面积计算技术.

埃及人的面积计算方法的基本思想是：任意一个直线多边形图形都可以分割为一些三角形，通过计算三角形的面积然后求和来解决问题.根据面积的定义，容易得到三角形面积计算公式是×底×高，到后来又有著名的海伦公式（其中），真正困难的具有挑战性的问题则是计算曲边多边形的面积.

首先碰到的一个典型的问题是圆面积的计算.

我们在圆周率讲座中了解到，古代刘徽和阿基米德都采用了一种所谓的“穷竭法”（以直代曲）来解决圆的问题，通过把圆无限分割，以多边形来逼近圆周.阿基米德用“双重归谬法”证明了命题：“圆的面积等于这样一个直角三角形的面积，直角边的一边是圆半径，另一直角边为圆的周长.”利用这个命题容易计算出圆的面积为πr2.

阿基米德利用凹凸镜聚光原理，将入侵叙古拉城的罗马船队烧个精光的故事大家都听说过，阿基米德对抛物线弓形也做过研究，并得到一个很有名的结果：

命题：一条抛物线弓形的面积是同底同顶点三角形面积的（如图8-1（1）所示）.

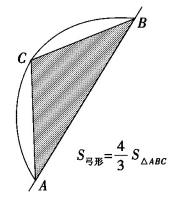
pagenumber_ebook=145,pagenumber_book=137

图8-1（1）

令人难以置信的是，阿基米德是从力学的角度首先得到这一结果的.

阿基米德被尊称为“数学之神”，无论以何标准举出数学史上最伟大的三位数学家，阿基米德都会被列入这个名单中.阿基米德的伟大之处还在于他那可贵的“理性思想”，相对于他对数学理论的研究，数学实验（如用测量法得出π的近似值，通过实验计算出皇冠上掺了多少假等）和数学应用（物理上的一些机械发明）在他看来都不是主流，只是一些雕虫小技罢了.而我们中学生们之所以知道阿基米德，更多在于他的一些物理上的发明，对阿基米德光辉的数学思想知之甚少，这想来也是很可笑的.

对于上面的那个命题，阿基米德是绝不会满足于从力学的角度来证明的.果然，他找到了数学上的依据：如图8-1（2），在抛物线弓形中作三角形ABC（同底同顶点），设其面积为S，阿基米德在以三角形两边为底的小抛物线弓形中再分别如法炮制地作内接三角形，并不断继续这个过程，他就获得了一系列边数不断增加的多边形，最后的这个多边形将铺满整个抛物线弓形.阿基米德通过特殊的数学技巧发现，随着边数的不断增加，多边形的面积以一个几何级数增加，即多边形的面积分别为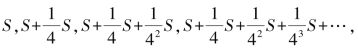 pagenumber_ebook=146,pagenumber_book=138 ……阿基米德算出最终的结果为.

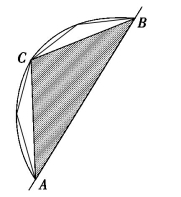
pagenumber_ebook=146,pagenumber_book=138

图8-1（2）

现代的我们可用无穷递缩等比数列求和公式，容易计算：

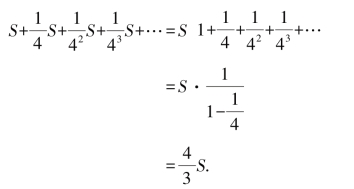
pagenumber_ebook=146,pagenumber_book=138

阿基米德通过把圆周无限分割，得到一个边数不断增加的多边形（其实也就是无数个三角形之和）；把抛物线弓形无限分割（用无数个三角形来铺满抛物线弓形），成功地解决了圆和抛物线弓形的面积的计算问题，沿着阿基米德们（这里当然也包括我国古代数学家刘徽、祖冲之们）开创的这种“穷竭法”，后来的数学家们继续前进，在德谟克利特的“原子论”的哲学思想的影响下，慢慢地把这种方法发展为一种非常有效的方法——“不可分量法”（即把一个图形无限细分，分到不能再分），理解这个思想是搞清楚“积分”概念的第一个关键.

例如，人们可以通过这样一种方法来“演示”圆的面积，假设圆是由无数个顶点位于圆心而底在圆周上的“小得不能再小”的三角形所组成（如图8-1（3）），每个三角形的面积都是底边长与高乘积的一半，对无数个“小得不能再小”的三角形而言，高都是圆的半径，所有三角形的底边之和就是圆周长，这样一来圆面积就是.

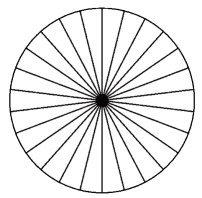
pagenumber_ebook=147,pagenumber_book=139

图8-1（3）

同样的道理，若我们将球面分成无数个“小得不能再小”的三角形（如图8-1（4）），则整个球体的体积为所有顶点在球心的三棱锥的体积之和，对无数个“小得不能再小”的三棱锥而言，所有三棱锥的高都是球的半径，所有小三棱锥的底面积的和就是球的表面积，这样一来，球的体积就是.

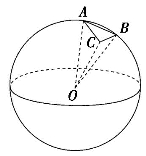
pagenumber_ebook=147,pagenumber_book=139

图8-1（4）

德谟克利特认为，世界万物都是由无限多个简单、永恒的原子组成的，这个哲学观对后来的数学家有着深刻的影响.数学家把这种观点引申到几何上，认为线是由点构成的，就像项链是由珠子穿成一样，面是由直线构成的，就像布是由线织成的一样，立体是由平面构成的，就像书是由纸组成的一样.在前面圆的情形中，所有分割点构成整个圆周，而要使小三角形的高都为圆的半径，只有当相邻两个分割点“重合”时才成立，在球的情形当中，无数个小三棱锥的底面将铺满球面，而要使所有三棱锥的高都为球的半径，只有当每个小三棱锥的底面三角形的三个顶点“缩为一点”时才成立.换句话说，圆中小三角形的底边和球中小三棱锥的底面都是一个“无穷小”.

天文学家开普勒（1571—1630）在探索行星运动的规律时，曾遇到如何确定椭圆扇形的面积和椭圆弧长的问题，开普勒利用“不可分量”的思想，系统地用“无穷小”方法来进行计算，也就是把给定的几何图形分成无穷多个无穷小的图形，然后用某种特殊的方法把这些图形的面积加起来，从而得到给定图形的面积.1609年，他在著作《新天文学》中给出了以下命题：

命题：若椭圆的半轴长分别为a和b，则椭圆的周长为π（a+b），椭圆的面积为πab.

圆显然是椭圆的一种特殊的情形.

开普勒还对表面为曲面的物体的体积的求法进行了广泛的研究，在其名著《酒桶新立体几何》中，论述了90多种表面为曲面的几何体体积的计算，这本著作被誉为所有求体积方法的灵感源泉.

但是，这种“不可分量法”似乎存在某种缺陷.一方面，“不可分元”通常被认为是一个无穷小的量，实际上也就是值为0的量，那么我们将无数个这种量相加，所得到的结果也应当为0（这里我们得到的是一个不定表达式∞×0，古代数学家一直头疼的“无穷大”“无穷小”再也回避不了了）；另一方面，这种方法对每个不同的问题都需要设计出相应的可行的“分割”方案，它需要很强的几何技巧以及分割后的代数求和技巧.然而，除了这些缺陷，这种方法又确实奏效，而且在很多情形下都会产生新的结果.开普勒是充分利用这种方法的先行者之一，在运用这些思想的同时，开普勒其实是在向现代积分学迈进.

人类文明进入17世纪，数学、物理学、天文学都进入了一个蓬勃发展的时期，这是一个英雄辈出的时代.就数学学科而言，一个重大事件的发生，成为数学发展的转折点，对整个科学界而言，其影响和意义都是不可估量的，这就是解析几何的创立.

解析几何把数学中的两个研究对象“数”与“形”统一起来，并在数学中引入“变量”，从而使运动进入了数学.解析几何利用坐标方法把带有两个变量的代数方程和坐标平面上的曲线联系起来，平面曲线与方程在坐标下建立了一一对应的关系.数与形之间的这座桥使两者的优点相结合，而丢弃它们各自的缺点，推动了数学的向前发展.

解析几何的创立，可以把阿基米德、开普勒等碰到的一些特殊的个体问题（解决这些个体问题都需要运用不同的特殊的技巧）全部归结于坐标系下的同一类问题，为一种新的计算系统创造了条件.笛卡尔和费马的功绩永载史册.

解析几何创立以前，关于求面积，有的只是一些漂亮、零星的发现.阿基米德关于抛物线弓形面积的论断就是一个很有名的、很了不起的命题.下面我们来看一看，如何在坐标系下解决曲边多边形的面积问题.我们先看一个简单的例子：

计算抛物线y=x2下方x=0到x=a区域内的面积.

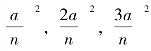我们用“不可分量法”来进行计算.如图8-1（5），将区间[0，a]分成n等分，共n-1个分点，每个分点的横坐标分别为，它们的纵坐标分别为 pagenumber_ebook=148,pagenumber_book=140 ……最右端点的纵坐标为，我们以这些纵坐标为高，以相同的分点间隔为底，构成n个矩形，当n无限增大时，这n个矩形的宽无限减小，构成此情形下的“不可分量”，我们对这些不可分量求和：

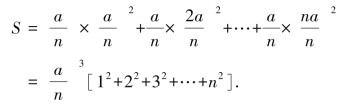
pagenumber_ebook=149,pagenumber_book=141

问题归结到一个著名的自然数的平方求和.而我们有，代入求和中可得： pagenumber_ebook=149,pagenumber_book=141 ，我们把它化简为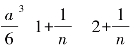的形式.

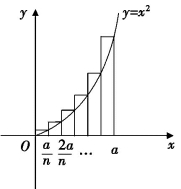
pagenumber_ebook=149,pagenumber_book=141

图8-1（5）(www.chuimin.cn)

最后，如果让“不可分量”的数目无止境地增大（也就是n→+∞），这时矩形的宽将趋近于零，矩形实际上成了线段（犹如线织成布），这时的值趋于0，这样我们得到所求面积为.

通过这个简单的例子，我们对如何利用“不可分量法”求面积有了一个直观的了解，同样的方法，我们可以求出y=x3在[0，a]上投影的面积（如图8-1（6）），我们有（n+1）2，故

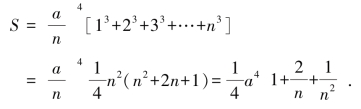
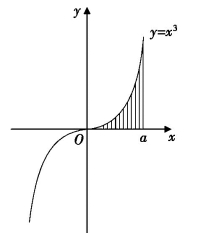
pagenumber_ebook=149,pagenumber_book=141

图8-1（6）

当n→+∞时，所求面积为.

以此类推，我们通过求和公式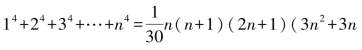 pagenumber_ebook=149,pagenumber_book=141 -1），可求得y=x4在[0，a]上的投影面积为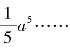由此我们可归纳出，对于广义抛物线y=xn（n为正整数），其在区间[0，a]上的面积为.

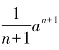这个结论非常重要，我们不能满足于用归纳法得出这个结论.但若按我们前面的分割求和法，最后将归结到序列1n+2n+3n+…+nn的求和，而这个求和是一个非常棘手的事情.

费马通过用一种巧妙的分割法绕过了这个困难的求和，成功地解决了这个问题.

问题：求抛物线y=xn（n为正整数）下方x=0到x=a区域内的面积.

费马把区间用无穷多个点（如K，L，M等）划分为无穷多个子区间，（如图8-1（7）），其中ON=a，然后从N点开始，逐步往左划分线段，使所得的线段依次呈几何级数递减（注意这里并不是等分），即

ON=a，OM=ar，OL=ar2，OK=ar3……（其中r是小于1的正数），这些点在曲线上所对应的高（即纵坐标）分别是an，（ar）n，（ar2）n……从右边第一个矩形算起，面积依次为：

这个序列构成一个以（1-r）an+1为首项，以rn+1为公比的无穷递缩等比数列，其和为

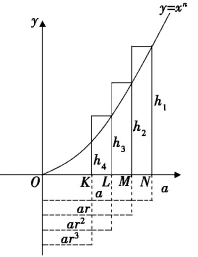
pagenumber_ebook=150,pagenumber_book=142

图8-1（7）

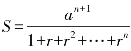最后的结果取决于r的值，费马意识到，要提高这些长方形面积之和与我们所求面积之间的吻合度，必须将每个矩形的宽缩减得更小，而要达到这个效果，比值r须从小于1的方向无限接近1，但当r取1时，表达式（1）变成了的一个不定式，但我们注意到1-rn+1=（1-r）（1+r+r2+…+rn），于是1-r可消去，表达式（1）变成 pagenumber_ebook=150,pagenumber_book=142 ，在r→1的情形下，分母中的每一项都趋近于1，这样就可求得.

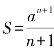费马的成果被看作一个意义重大的突破，因为它解决了一类曲线（而不是一条曲线）的求积问题，特别是费马进一步把n从正整数推广到负整数，结论依然成立（n=-1除外）.

沿着开普勒、费马、帕斯卡们的足迹，随后的牛顿和莱布尼茨登上了历史的舞台.

牛顿在1669年所写的《无穷级数分析》一书中系统地论述了求面积的方法，牛顿不仅把费马的重要的求面积的公式做了推广，还在书中给出了求“简单曲线的面积”的三个法则.牛顿的三条法则其实就是积分法则.

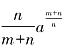法则1：简单曲线的面积，如图8-1（8）中，如果是曲线AD的函数，m和n是正整数，那么区域ABD的面积为 pagenumber_ebook=151,pagenumber_book=143 ，这样，牛顿就把“费马公式”中的指数从整数推广到了分数.

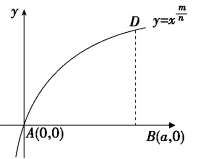
pagenumber_ebook=151,pagenumber_book=143

图8-1（8）

牛顿的第二个法则论述了有限项和的积分等于各项积分的和，而第三个法则断言当遇到更复杂的函数表达式时，可以将其“化简”成无穷级数，再通过第一条法则对级数的每一项求积分，然后再由法则二对结果求和（参见第一讲牛顿的π的似近值）.

有了前面的铺垫，积分的定义呼之欲出.

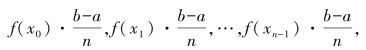如图8-1（9）所示，为求曲线y=f（x）下方从a到b的区域K的面积，我们将x的区间[a，b]n等分，依次为x0（a），x1，x2，…，xn-1，xn（b），在各点上作x的垂线，以各个小区间左侧的高作长方形，于是区域K就被分割成n个长方形.长方形的宽都是，于是它们的面积分别为： pagenumber_ebook=151,pagenumber_book=143 当n→+∞时，宽度趋近于0（长方形成为线段），长方形面积和的极限值表示为算式.

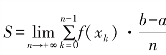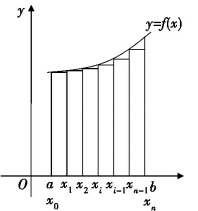
pagenumber_ebook=151,pagenumber_book=143

图8-1（9）

若每个分点的间隔用Δx表示，则.

我们定义这个和为函数f（x）在[a，b]上的定积分，它的含义就是区域K的面积.

17世纪中叶，莱布尼茨赋予积分一种新的表示符号，如图8-1（10），假定我们要计算曲线AB下面的面积，莱布尼茨将这个区域的面积想象成由无限多个无限小的矩形构成，给动点x一个增量dx，把每个矩形的宽度用dx表示，而高度为y（y=f（x），其中y随曲线AB的形状变化而变化），那么无限小矩形的面积为y·dx，莱布尼茨对这无穷多个面积求和，他选用伸长的“S”——代表summa（求和）——作为表示这个求和过程的记号，这个面积就表示成了∫ydx，从此以后，他的积分符号成为一种标志，向所有见到它的人宣告微积分时代的来临.

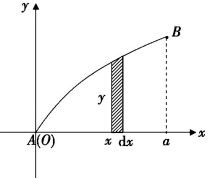
pagenumber_ebook=152,pagenumber_book=144

图8-1（10）

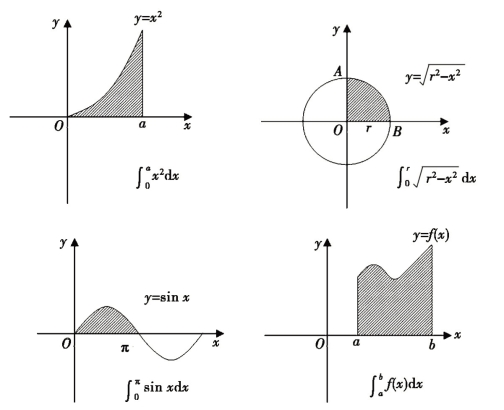
莱布尼茨的积分符号“∫”取代了求和符号“∑”，它代表的是一个求和的过程.用莱布尼茨的积分符号，图8-1（11）中各个阴影部分的面积可分别表示为 pagenumber_ebook=152,pagenumber_book=144 ，这个表示法简洁、明了.

pagenumber_ebook=152,pagenumber_book=144

图8-1（11）

但提出一个表示面积的记号是一回事，而如何计算它完全是另一回事，如果光有这个记号，在计算时还要回到“分割-求和”的老路上去，那莱布尼茨也就不能成为莱布尼茨了.这里的关键是莱布尼茨不仅提供了一个好的符号表示，更重要的是他还发明了一种新的计算方法.讲到这里，我们仿佛看到了另一路数学大军正向我们赶来，这就是下面我们要了解的——微分.

积分：数学未被遗忘的进化

相关推荐