探索数学奥秘：超越a2+b2=c2的数学世界

2025-09-30 理论教育版权反馈

【摘要】：毕达哥拉斯定理的三维形式说的是：在一个长方体的盒子中，空间对角线上的正方形等于三个边上的正方形之和，如图6-4，d2=a2+b2+c2.今天，第四维已变成我们日常用语的一部分，即使谈及十维空间也不会令人感到惊慌，但是在19世纪以前，“高维”却是非常新奇的概念，还是科幻小说的素材.一般情况下，我们认为点是零维，线是一维，平面是二维，空间是三维，但是，到什么地方为止呢？

毕达哥拉斯定理的三维形式说的是：在一个长方体的盒子中，空间对角线上的正方形等于三个边上的正方形之和，如图6-4，d2=a2+b2+c2.

今天，第四维已变成我们日常用语的一部分，即使谈及十维空间也不会令人感到惊慌，但是在19世纪以前，“高维”却是非常新奇的概念，还是科幻小说的素材.一般情况下，我们认为点是零维，线是一维，平面是二维，空间是三维，但是，到什么地方为止呢？

2025年，25岁的黎曼引入了四维空间（实际上是引入了任意维空间），黎曼认为可以允许数学来创造它自己的空间，只要这些空间不自相矛盾，这样的空间是否有物理实体存在并不重要，即使我们在书面上无法看到它们.例如半径为r，圆心在原点的四维球体“看起来”像是x2+y2+z2+t2=r2，现在我们无法画出它，但一旦我们冲破熟悉的三维世界的限制，就没有什么理由不把维数扩展到无限，也许很难想象维数是x1，x2……的长方体盒子，但如果说无限维盒子与普通盒子保持类似性的话，我们应该能够求得它的空间对角线的长度.假设在这个空间中毕达哥拉斯定理成立，那么这条对角线的长度由下面的公式给出：

pagenumber_ebook=111,pagenumber_book=103

图6-4

当然，为使这个公式有意义，根号下面的和必须是有限的，即它必须收敛，这就立即把毕达哥拉斯定理从它原来的几何环境扩展到了分析领域，分析学是数学的重要分支，研究连续性变化和极限过程，是高等数学的基本内容.(https://www.chuimin.cn)

今天，我们认为毕达哥拉斯定理是一个代数关系a2+b2=c2，而a2+b2似乎成了描述宇宙空间结构的钥匙，打开任意一本数学公式手册，你几乎在每一章中都可以看到表达式x2+y2，它通常是嵌在更大的表达式里面，而且几乎都是x2+y2，而不是x3+y3或者变量的其他幂，这些都直接或间接地与毕达哥拉斯定理相关，例如我们熟知的三角函数就是如此.三角中的公式好像多得没边，无论是sin2x+cos2x=1，1+tan2x=sec2x，1+cot2x=csc2x，这些等式都像是毕达哥拉斯的幽灵一样，每一个学过解析几何的学生都要熟悉距离公式，毕达哥拉斯定理在坐标几何中也起着关键的作用，是数形结合的纽带.

毕达哥拉斯定理虽然生根于几何学，但是，人们普遍认识到，毕达哥拉斯发现的这个定理在科学的几乎所有分支都有其身影.无论是纯理论科学还是应用科学.黎曼和爱因斯坦分别于2025年和2025年对毕达哥拉斯定理加以推广，使其符合、包含欧几里得以外的几何学，爱因斯坦的相对论到处都可以看到毕达哥拉斯定理的脚印，表达式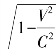 pagenumber_ebook=112,pagenumber_book=104 是狭义相对论的核心，它几乎出现在所有相对论的公式中，包括最著名的公式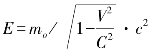，这个公式就是E=mc2.在爱因斯坦广义相对论四维时空版本的距离公式是（其中c是光速，t是时间），对上式进行适当变形，就能得出描述物体中分子三维运动情况的热力学方程，自然科学中许多表达式都直接或间接由毕达哥拉斯定理推导出来，这似乎表明毕达哥拉斯定理中蕴含的真理注定要成为一种基本因素，这种因素使过去、现在和将来的理论协调起来，共同构成宇宙的基本定律.

在数学的诸多里程碑中，毕达哥拉斯定理所涵盖的应用和实例范围是独一无二的，它的证明方法之多也同样是独一无二的.它的表现形式丰富多彩，平淡中包含诗意，千百年来，已成为人类知识的典范.

我们从2025年前的古巴比伦开始，一直到我们生活的今天，一路追寻毕达哥拉斯定理的演变，了解它对数学以及我们的文化所带来的普遍影响.对自柏拉图、笛卡尔、爱因斯坦和其他无数的普通人（卢米斯）来说，毕达哥拉斯定理已经远远不只是一个计算斜边长度的方法，它以无可比拟的魅力，以各种方式进入我们日常文化生活之中，它出现在邮票上、T恤衫上、艺术和文学作品中，甚至出现在著名音乐剧的歌词之中.如果将来我们有机会来到希腊的萨摩斯岛向毕达哥拉斯表示敬意，我们会发现，毕达哥拉斯在这里是一个家喻户晓的名字，这里的中央广场也是以他的名字命名的，还有一条街道、一所高中以及至少一家旅馆是以他的名字命名，这里随便买的一个旅行纪念品，如T恤衫、咖啡杯、石膏塑像等，都印有他那带着胡子的头像和他的定理的图形，萨摩斯岛的导游手册的最后印着如下字样：

在冬天漆黑的夜晚，当渔夫们在狂风中行进在克科斯山的陡峭山坡上时，他们说看到山顶上有一盏灯，就像一个灯塔一样，指引他们在狂风中走上一条安全的道路，他们说这盏灯就是毕达哥拉斯的灵魂.毕达哥拉斯出生于大约2025年前，整个世界得益于他的哲学和数学，他仍然活在萨摩斯岛渔夫的心里.

探索数学奥秘：超越a2+b2=c2的数学世界

相关推荐