据传毕达哥拉斯学派为庆祝该定理的发现曾宰杀百牛祭祀缪斯女神,但这与该学派所奉行的素食主义相悖。后人对毕达哥拉斯发现和证明勾股定理有各种猜测。图3.2.14毕达哥拉斯定理图3.2.15毕达哥拉斯定理的证明一般认为,毕达哥拉斯采用了剖分方法来证明定理。因而就有化简后则得到毕达哥拉斯定理。《几何原本》中的毕达哥拉斯定理图3.2.16毕达哥拉斯纪念碑3.2.17《几何原本》命题473.2.18希腊1955 年邮票毕达哥拉斯定理是《几何原本》第一卷命题47。......
2023-11-23
371种毕达哥拉斯定理证明
【摘要】：或许在整个数学中，还找不到另一个定理，其证明方法之多能够超过毕达哥拉斯定理，不同的时代，不同的国家和地区，不同职业的人物都在寻找定理的新的证明方法.据说，在中世纪，要求取得数学学位的学生必须提供毕达哥拉斯定理的原创证明，这激发了学生和老师们不断提供新的、有创意的证明方法.美国克里夫兰西部高中数学教师卢米斯（1825—1940）在他做教师的50年间，收集整理了毕达哥拉斯定理的371种证明，出版了一本
或许在整个数学中，还找不到另一个定理，其证明方法之多能够超过毕达哥拉斯定理，不同的时代，不同的国家和地区，不同职业的人物都在寻找定理的新的证明方法.据说，在中世纪，要求取得数学学位的学生必须提供毕达哥拉斯定理的原创证明，这激发了学生和老师们不断提供新的、有创意的证明方法.美国克里夫兰西部高中数学教师卢米斯（1825—1940）在他做教师的50年间，收集整理了毕达哥拉斯定理的371种证明，出版了一本285页的《毕达哥拉斯命题》著作，这使不大可能出名的中学教师成了一位名人.
下面的内容是卢米斯著作中的精彩片段，简单给大家介绍一下.
1.最短的证明
如图6-3（1），根据射影定理，显然有b2=AD·c，a2=BD·c，两式相加即可.
图6-3（1）
这就是欧几里得的第二个证明.（第六卷的第31个命题）
2.利用相似的性质证明
如图6-3（2），因为图中的三个直角三角形两两相似，
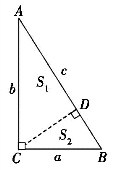
图6-3（2）
因而
，两式相加即可.
3.利用切割线定理证明
如图6-3（3），以B为圆心，BC为半径作圆交AB于P，延长PB交圆于Q，由切割线定理有AC2=AP×AQ⇒b2=（c-a）（c+a），即有c2=a2+b2.
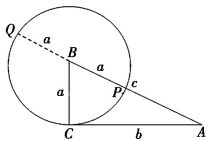
图6-3（3）
4.一个基于旋转的证明
把直角三角形三边（三边分别为a，b，c，假设a＞b）补成一个边为a的正方形（图6-3（4）），
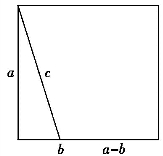
图6-3（4）
关于这个三角形的上顶端按逆时针方向旋转90°（图6-3（5）），
图6-3（5）
然后再清除原来的三角形产生了一个四边形（图6-3（6））.
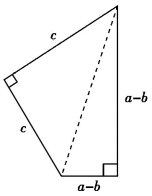
图6-3（6）
显然它的面积等于正方形的面积，因此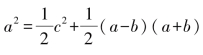
，化简，得到a2+b2=c2.(www.chuimin.cn)
如图6-（7），延长CB至D，使BD=AC=b，作DE⊥BD，且使DE=BC=a，连接BE和AE，构成一直角梯形ACDE，显然，利用面积
图6-（7）
c，得到a2+b2=c2.
这一证明之所以出名，是因为它是由美国第20任总统詹姆斯·加菲尔德提出的，这一证明是总统先生1876年当议员时与其他国会议员在一次数学讨论中偶然发现的。
欧几里得在《原本》卷Ⅲ中给出了一些关于圆的命题，可以利用圆的性质来证明毕达哥拉斯定理。
6.最长的证明
最长的证明是法国数学家勒让德给出的，勒让德在比例式中兜圈子，实在没有必要，因为太长，所以不想在这里把完整的证明展现出来.
卢米斯的《毕达哥拉斯命题》共收集了371个证法，有几何证法、代数证法、动态证法等多种不同的形式，其中大部分都是几何证法，证法的提供者有数学家，有名人（如第31种证法是惠更斯给出的，第53种证法是莱布尼茨给出的，第225种证法是婆罗门笈多给出的，等等），也有普通的数学爱好者和中学生（如1938年印第安纳州高中女学生安·康迪给出的一个相当精巧的证明，甚至盲人姑娘也给出了一个原创证明），卢米斯在他著作第二版的最后一句话是“新的证法没有尽头”.
好了，对于毕达哥拉斯定理，我们现在已有几百个证明它的方法，还有什么要说的吗？
作为“伟大的定理”，当然还有很多内容，例如，没有哪个定理能像毕达哥拉斯定理那样衍生出如此多的注释、变形和应用.其中有一些是显而易见的，而另外一些则比较深奥.
在“风车”证明的那个图中，其实我们也可以用任意图形——多边形或非多边形，来取代直角三角形边上的正方形，只要它们相似就可以了.如图6-3（8）给出了五边形的情形，图6-3（9）给出了以各边为直径的半圆形的情况.
图6-3（8）
运用于正五边形的毕达哥拉斯定理Sc=Sa+Sb
古希腊的文明史，自伟大的泰勒斯，经历毕达哥拉斯学派，它最辉煌的年代开始于公元前387年左右，当时柏拉图建立了雅典学园，这所学园统治了希腊文化生活近千年.柏拉图自己虽然不是一名数学家，但是他对数学的重要贡献是他认识到掌握逻辑思想的重要性以及最终建立健全的民主的重要性，雕刻在这所学园门口的座右铭“不懂几何者不得入内”成为一句不朽的名言，欧几里得受柏拉图学园的深刻影响，他编纂的《几何原本》成为数学的“圣经”.
继欧几里得之后，古希腊数学史中下一个伟大的名字是阿基米德（公元前287—前212），他使希腊数学的黄金时代达到了顶峰.当然，其后还有很多著名的学者，如阿波罗尼奥斯（研究圆锥曲线），丢番图（研究数论和方程），希帕克斯（三角学的创始人）以及托勒密，他的巨作《至大论》概括了那个时代已知的世界版图，这是以地球为中心的宇宙，在这个宇宙里，太阳、月亮、行星和其他星星以完美的圆形轨道围绕地球运动.
希腊数学漫长的历史长河中最后一位令人注目的数学家是帕普斯，大约生活在公元3世纪，他为欧几里得的著作做了注释，他的《数学汇编》共八卷，包含很多优美、富有创意的结果.其中一个定理是毕达哥拉斯定理的一个扩展：
如图6-3（9），设△ABC是任意三角形，四边形ABDE和ACFG是构建在边AB和AC上的两个平行四边形，延长DE和FG相交于H，分别作平行且等于HA的BM=CN，这产生一个平行四边形BMNC，帕普斯定理指出，这个平行四边形的面积等于原来的平行四边形面积的和.
图6-3（9）
运用于半圆的毕达哥拉斯定理Sc=Sa+Sb
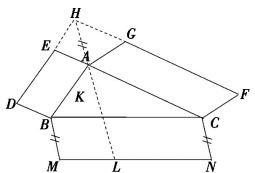
图6-3（9）
这个定理的证明思路类似于欧几里得命题47中的毕达哥拉斯定理的证明，留给大家课后练习.显然，毕达哥拉斯定理是这个定理的特殊情况，其中∠BAC是直角，且图中的平行四边形是正方形.
有关被遗忘的数学课的文章
- 详细阅读
-
罗尔定理的证明和费马定理的基本性质详细阅读
从几何上可以看到：在对于两端高度相等的连续光滑曲线上，必存在一条水平的切线（如图3－1所示），这便是罗尔定理.为了罗尔定理证明的需要，下面先给出极值的定义和极值点的一条基本性质——费马定理.图3－1定义1设f（x）在点x0的某邻域内有定义，若x∈（x0，δ），恒有f（x）＜f（x0）（或f（x）＞f（x0）），则称f（x0）为f（x）的一个极大值（或极小值），函数的极大值与极小值统称为函数的极值......
2023-11-19
-
正交子空间定理及证明详细阅读
定义6.6 若V1和V2是欧氏空间V的子空间，且对任意的α∈V1，β∈V2，总有<α，β>=0，则称子空间V1与V2是正交的.如果同时还有V1⊕V2=V成立，则V2就称为V1的正交补空间，记作V2=V1⊥.同样地，此时V1也是V2的正交补空间.定理6.3n维欧氏空间的任意子空间都有唯一的正交补空间.证明：设W是n维欧氏空间V的一个子空间，如果W是零维的，无须证明.现设dimW>0，选取W的一组正交基α1，α2，…......
2023-11-22
-
毕达哥拉斯学派及其贡献——毕达哥拉斯定理与带详细阅读
这是毕达哥拉斯纪念碑,碑体呈直角三角形形状．毕达哥拉斯是古希腊哲学家、数学家,创建了宗教、政治、学术合一的著名的毕达哥拉斯学派,该学派信奉“万物皆数”,发现了毕达哥拉斯定理,定义了奇数、偶数、完全数、亲和数等概念,研究了图形数的规律．知能概述用一个正整数b去除另一个正整数a,若商为q,余数为r,则有a＝bq＋r．余数有以下基本性质:b|(a－r);一个正整数a被另一个正整数n(n＞1)除时,余数只可能是0,1,2,…......
2023-08-13
-
毕达哥拉斯定理：数学课中的珍宝详细阅读
费马的研究是建立在自毕达哥拉斯以来一直到他的时代大量知识的基础上的.费马在数论领域的第一个发现涉及所谓的“亲和数”.亲和数是这样的一对数，其中的一个数是另一个数的因数之和，如早期的毕达哥拉斯学派得到的220和284（其中220的因数有1，2，4，5，10，11，20，22，44，55，110，它们的和是284；另一方面，284的因数是1，2，4，71，142，它们的和是220），直到1636年才由......
2023-11-19
- 详细阅读
-
毕达哥拉斯定理：一本书揭示科学发现史详细阅读
毕达哥拉斯学派将算术和几何紧密联系起来。毕达哥拉斯学派最大的贡献在数学方面，最著名的就是“毕达哥拉斯定理”，该定理在中国称为勾股定理，即直角三角形斜边的平方等于两直角边的平方和。而毕达哥拉斯定理的发现，实际上导致了无理数的发现，尽管毕达哥拉斯学派不愿意接受这样的数，并因此形成了数学史上所谓的第一次数学危机，但是毕达哥拉斯学派的探索仍然是功不可没的。不过毕达哥拉斯定理的证明，还应归功于毕达哥拉斯。......
2023-08-16
-
毕达哥拉斯定理的发现与世界各地的数学成果详细阅读
与人类文明的其他重要成就一样，毕达哥拉斯定理的发现不是某个人在某个时刻的灵光闪现，不同的国家和地区的人们在不同的时期，各自独立地得到这一发现.我国现存最早的有关天文学和数学的著作是《周髀算经》，成书年代大概在公元前2世纪，而书中的内容当然还要早.据记载，商高在回答周公关于数学计算的问题时答曰：“……故折矩，以为勾广三，股修四，径隅五……”......
2023-11-19
相关推荐