欧几里得的贡献与毕达哥拉斯相似

2023-11-19 理论教育版权反馈

【摘要】：与毕达哥拉斯一样，我们对欧几里得的生平知之甚少.他很可能出生在雅典，并在那里著名的柏拉图雅典学园接受教育，随后，他定居亚历山大城，成为亚历山大大学的数学带头人.欧几里得写了几本数学和光学的书，其中有一些经由阿拉伯人的翻译而保存下来.他最具影响力的著作是《几何原本》.这一著作共分为十三卷，是他所处时代数学论述的汇总.机会难得，这里我们把《几何原本》做一个简要的概述，梳理一下线索，这对我们理解毕达哥拉

与毕达哥拉斯一样，我们对欧几里得的生平知之甚少.他很可能出生在雅典，并在那里著名的柏拉图雅典学园接受教育，随后，他定居亚历山大城，成为亚历山大大学的数学带头人.欧几里得写了几本数学和光学的书，其中有一些经由阿拉伯人的翻译而保存下来.他最具影响力的著作是《几何原本》.这一著作共分为十三卷，是他所处时代数学论述的汇总.

机会难得，这里我们把《几何原本》做一个简要的概述，梳理一下线索，这对我们理解毕达哥拉斯的“证明”的思想很有必要.

欧几里得以“定义、公理、定理和证明”为线索，把自毕达哥拉斯以来发展起来的数学聚集成一个符合逻辑的巨大的数学体系.《几何原本》的开篇给出了23个基本概念，例如点（没有整体的部分）、线（由点组成的平坦的线，没有宽度）等，这之后是10个陈述，欧几里得认为这10个陈述清楚明了没有疑问，因此无须证明.今天，我们把这些陈述称为公理，并把它们分为两组：第一组的5个公理是研究几何概念的，即书中所谓的“公设”，其余5个公理是研究算术的.即书中所谓的“公理”，我们把它们一一列举出来：

公设：

1.过任意两点可作一条直线；

2.直线可向两端无限延伸；

3.以任意一点为圆心及任意距离为半径可画一个圆；

4.所有的直角均相等；

5.一条直线与另两条直线相交，若同一侧的内角和小于两个直角，则将这两条直线无限延伸，它们在小于两个直角的一侧相交.

公理：

1.与同一个量相等的所有量彼此相等；

2.等量加另一等量，和相等；

3.等量减另一等量，差相等；

4.彼此能够重合的物体彼此全等；(www.chuimin.cn)

5.整体大于部分.

准备工作做好了，接下来的就是推理，欧几里得推理的武器主要是苏格拉底的“所有人都会死，苏格拉底是人，所以苏格拉底会死”的所谓逻辑“三段论”和“苏格拉底是人，同时苏格拉底又不是人，不能同时正确”的逻辑排中律.

在这些简洁、精炼的23个定义和10条公理的基础上，欧几里得以“逻辑”为依据，推导出来465个定理.在此接下来的2000多年里，这个知识体系被尊为绝对的真理、神圣的典据而传递下来，简洁的风格和严格的逻辑论证使这本书吸引了很多伟大的思想家，成为以后所有数学著作的典范，没有任何一本书像《几何原本》那样对数学产生了如此巨大的影响.

欧几里得将前48个定理（命题），组成《几何原本》第一卷，这一卷中涵盖了我们现在所学的平面几何的一些基本内容，如在给定三角形的一条边的条件下，如何构造一个等边三角形，如何复制一条线段（也就是说在平面内如何把一条线段移到一个新的位置上），如何从直线外一点作这条直线的垂线，如何平分一个角，等等.在这一卷中，我们还可以看到我们熟悉的三个全等定理（SAS，SAA和SSS）以及三角形内角和等于两个直角的定理，共46个，接着，欧几里得在第一卷的末尾表述的是：

命题47：在直角三角形中，直角的对边上的正方形等于包含这个直角的两条边上的正方形.

也就是说，斜边上的正方形的面积等于两条直角边上的正方形的面积之和，这就是毕达哥拉斯定理.（《几何原本》中任何地方都没有出现与特殊定理相关的人的名字，毕达哥拉斯的名字也不例外）

请大家注意一下，欧几里得的命题不是表述代数方程式c2=a2+b2，而是表述了一种几何现象：面积.为证明这一个命题，他采取了一个非常巧妙的方法：如图6-2，从直角顶点作线段AL，使之与大正方形的边平行，并将大正方形分割成两个矩形.然后欧几里得只要证明左边的矩形面积S四BMLD等于以AB为边的正方形面积，右边矩形的面积S四MCEL等于以AC为边的正方形面积，因两个矩形面积之和等于大正方形面积，由此可导出，大正方形面积等于两个小正方形面积之和.

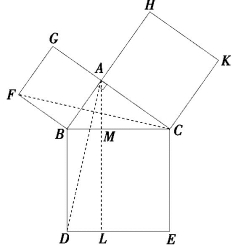
pagenumber_ebook=106,pagenumber_book=98

图6-2

这一证明方法非常巧妙，但还需补充很多细节，当然，欧几里得在他前面的46个命题中早已完成了全部的准备工作，我们简单描述一下证明的逻辑链：

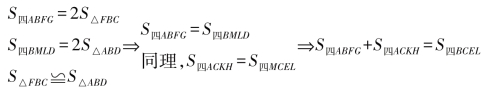pagenumber_ebook=106,pagenumber_book=98 ，证毕.

虽然我们的表述很简练，但对于刚刚开始学习几何的初中生来说，这个定理的证明肯定是他们遇到的最难的证明之一.欧几里得为什么要选择这样一个很难的证明呢？这里有两种可能的情形.一个理由是当时的希腊人把所有算术运算都翻译成与几何相关的内容：数被看成一条线段的长度，两个数的和被看成端点相接的两条线段的总长度；两个数的积被看成以相应线段为边的矩形的面积；三个数的积被看成以相应线段为边的立方体的体积，因此欧几里得很自然地把毕达哥拉斯定理解释成为面积关系，而欧几里得的“风车”证明是他们所能想象出的面积表示的唯一方法.另一个理由是欧几里得显然意识到他的证明给读者带来的困难，所以在后面的第六卷中，欧几里得运用相似理论给出了第二种证明方法.但是比例法要到《几何原本》的第五卷才给出，因而相似法要到第六卷给出，但是，欧几里得显然不愿意把这样一个重要的定理的证明放在第六卷，“风车”证明虽然难些，但它必须放在第一卷，所以在“知识储备”最少的情况下，在《几何原本》的逻辑链条体系中，欧几里得把他的“风车”证明放在第一卷的最后，作为他第一卷的高潮和压轴，这也充分体现了欧几里得对这个定理的重视和偏爱.

尽管《几何原本》中的命题47不曾以毕达哥拉斯的名字命名，但欧几里得还是以这种特殊的方式，含蓄地向大师表达了敬意.《几何原本》的其余部分中经常使用这个定理，有关命题47的证明在随后的时代增加到了上百个，由于欧几里得，毕达哥拉斯定理开始传播开来.

欧几里得的贡献与毕达哥拉斯相似

相关推荐