这是毕达哥拉斯纪念碑,碑体呈直角三角形形状.毕达哥拉斯是古希腊哲学家、数学家,创建了宗教、政治、学术合一的著名的毕达哥拉斯学派,该学派信奉“万物皆数”,发现了毕达哥拉斯定理,定义了奇数、偶数、完全数、亲和数等概念,研究了图形数的规律.知能概述用一个正整数b去除另一个正整数a,若商为q,余数为r,则有a=bq+r.余数有以下基本性质:b|(a-r);一个正整数a被另一个正整数n(n>1)除时,余数只可能是0,1,2,…......
2025-09-29
与人类文明的其他重要成就一样,毕达哥拉斯定理的发现不是某个人在某个时刻的灵光闪现,不同的国家和地区的人们在不同的时期,各自独立地得到这一发现.我国现存最早的有关天文学和数学的著作是《周髀算经》,成书年代大概在公元前2世纪,而书中的内容当然还要早.据记载,商高在回答周公(约公元前2025年,周武王之弟)关于数学计算的问题时答曰:“……故折矩,以为勾广三,股修四,径隅五……”这就是商高定理或勾股定理名称的由来.《周髀算经》本文没有给出勾股定理的证明,但《周髀算经》赵爽(字君卿,大约生活在公元3世纪,后汉三国时期)注中的“勾股圆方图”中,蕴含了迄今所知中国古代最早的勾股定理的证明,如图6-1(1),我们用现代语言表示,从![]() 就可推出勾股定理.2025年8月20日,世界数学家大会首次在中国举行,大会所使用的会标就是这个赵爽弦图.
就可推出勾股定理.2025年8月20日,世界数学家大会首次在中国举行,大会所使用的会标就是这个赵爽弦图.
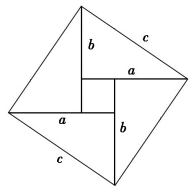
图6-1(1)
古印度人很早就知道这个定理,从印度典籍《绳法经》一书中可以找到它的应用.该书与佛经同时问世,约成于公元前500年到公元前100年,当然它所传授的知识也可追溯到更早以前.虽然书中的表达常常是不正式的、粗糙的,也没有提供什么证明,但它却为宗教建筑的建造提供了大量相关的几何知识.
毕达哥拉斯定理对描述空间起着至关重要的作用.木匠、建筑师和测绘师在建设小型和大型工程时都离不开它.古代的工匠通过实践发现,直角三角形的三条边是由特定的数组构成的,例如3,4和5或者5,12和13,这些三元数组称为毕达哥拉斯三元数组.远在公元前2025年,古巴比伦人的楔形文字泥板(这块泥板现收藏在美国哥伦比亚大学,称为普林顿322号)上就已经有了15行毕达哥拉斯三元数组组成的表.毫无疑问,表中通过一系列的例子对定理进行了验证.
所以早在毕达哥拉斯以前一千多年,或至少可以追溯到毕达哥拉斯时代,世界各地的人们就已经知道了这个定理,那么,为什么传说中都把这个定理归功于毕达哥拉斯呢?正如口头禅所说的“言必称希腊”一样,还是让我们透过历史的迷雾,了解一下毕达哥拉斯以及他神秘的学派吧.
毕达哥拉斯大约于公元前570年出生于希腊爱琴海的萨摩斯岛,这个小岛以东一个名叫米利都的海岸城镇里住着著名的哲学家泰勒斯,他是为后世创立知识体系的希腊第一学者,年轻的毕达哥拉斯在这位大师的指导下学习,他点燃了毕达哥拉斯对数学和哲学的热情.而后,毕达哥拉斯开始游历于古代世界文明的圣地,其中包括埃及和波斯,尽可能地从那里汲取当地的文学、宗教、哲学和数学知识,这期间学到的东西对这位年轻的学者产生了深刻的影响.
公元前530年,毕达哥拉斯离开萨摩斯岛,在一个叫克罗顿的偏远希腊村落(现意大利东海岸)定居.在那里,他创办了一所学园,在导师的指导下,这些毕达哥拉斯信徒们学习了当时存在的所有学科的知识,特别是哲学、数学和天文学.但是,这不仅仅只是一所学园,他们还建立了一个教派,也就是一个要求成员间彼此相互忠诚的“兄弟会”,毕达哥拉斯信徒按照东方的传统,通过口口相传进行知识传播,只留下极少数的文字,这可能也是毕达哥拉斯学派显得很神秘的原因之一吧.出于对他们领袖的尊重,这些信徒所做的很多发现都被归功于毕达哥拉斯本人,而真正的发现者几乎不为人所知.
毕达哥拉斯建立“兄弟会”后不久,撰造了一个名词“哲学家”,在一次出席奥林匹亚竞技会时,弗利尤斯的利昂王子问毕达哥拉斯他如何描述他自己,毕达哥拉斯回答道“我是一个哲学家”.利昂王子以前没听说过这个词,因而请他解释:
“利昂王子,生活正好比这些公开的竞技会.在这里聚集的一大群人中,有些人受奖励物的诱惑而来,另一些人则因对名誉和荣耀的追求的驱使而来,但他们中间也有少数人来这里是为了观察和理解这里发生的一切.
生活同样如此.有些人因爱好财富而被左右,另一些人因热衷于权力和支配而盲从,但是最优秀的一类人则献身于发现生活本身的意义和目的.他们设法揭示自然的奥秘.这就是我称之为哲学家的人.虽然没有一个人在各方面都是很有智慧的,但是他能热爱知识,视其为揭开自然界奥秘的钥匙.”
“兄弟会”实际上是一个宗教性社团组织,他们崇拜的偶像之一是数,他们相信,通过了解数与数之间的关系,他们能够揭示宇宙神圣的秘密,使他们自己更接近神.他们开始将注意力集中于“计数数”和分数的研究,在这无穷多个数中间,他们寻找那些有特殊重要意义的数,如所谓的“亲和数”“三角形数”“象形数”等.当然,他们在研究数与数之间的所有关系中,最重要的是以他们的奠基者命名的那个关系,热衷于寻找满足a2+b2=c2的正整数(也就是3个边都是整数的直角三角形),并成功地找到了所谓的“毕达哥拉斯三元组”模式(若n为奇数,n,![]() ,和
,和![]() 形成一个毕达哥拉斯三元组).
形成一个毕达哥拉斯三元组).
除了研究数之间的关系外,数与自然的关系也是他们的研究重点,当他们了解到从音乐的和声到行星的轨道等一切事物中都藏有数时,他们认识到所有自然现象都是由规律支配的,而这些规律可以用数字关系来描述,显示了数学与科学之间、数学与宇宙、自然之间有着根本的关联,这致使“万物皆数”成为毕达哥拉斯学派的信仰和基石.
毕达哥拉斯创造了“哲学家”一词,并以哲学家自居并非浪得虚名.由于毕达哥拉斯的天才,他深邃的思想远远超越他同时代的人们.在他看来,“数”不再是仅仅用来记账和计算,虽然他提出了“万物皆数”的理论,宇宙万物、自然规律皆能用数来描述,但他更认识到“数”本身的价值,认识到数独立于有形世界而存在,因而对数的研究就不会因感知的差错而受影响,这意味着他能发现独立于人们的印象或偏见的真理,这种真理比以前的任何知识更为绝对无疑.
古埃及人和巴比伦人把数学看作一种解决问题的工具,只要计算给出正确的答案,没有人会费神去怀疑这种计算方法或者去寻求隐藏在这些方法背后的逻辑.对这些文明古国来说,重要的是计算有效——至于它为什么有效则是无关紧要的.
如图6-1(2),测量的结果斜边一定是5;对图6-1(3),测量的结果斜边一定是13……但是他们无法证明a2+b2=c2这个关系对于他们尚未测试的所有直角三角形都是对的.
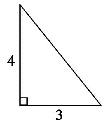
图6-1(2)

图6-1(3)(https://www.chuimin.cn)
那么毕达哥拉斯怎么知道这个定理对于每一个直角三角形都是对的呢?他和中国人或古巴比伦人一样,不可能去测试无限个不同的直角三角形,然而他仍然百分之百地确信这个定理绝对正确,使他有这种信念的理由是他用数学“证明”了这个结论.
寻找一个数学证明就是寻找一种认识,这种认识比任何别的训练和经验所积累的认识都更加不容置疑,对毕达哥拉斯来说,数学证明的观念是神圣的,一个被证明了的数学结果具有比任何别的真理更可靠的真实性.
“伟大的定理”归属毕达哥拉斯的理由是他第一个“证明”了它的普遍正确.定理为我们提供了一个方程,它对一切直角三角形都成立,因而它也定义了直角
三角形本身,同时,直角也定义了垂直(即竖直)与水平的关系,定义了我们生活着的空间结构.
“毕达哥拉斯定理”一词其实包含了两个含义,一个是法则,另一个是证明.法则叙述的仅仅是事实,说明直角三角形各边长之间的关系,该法则有实用的价值,但是证明就不同了,它陈述的是人们如何知道这个事实是正确的,与定理的实际用途无关.毕达哥拉斯的“证明”标志着人们对数学的思考方式发生了根本的变化,这种变化标志着数学从古代经验主义到现代数学(演绎学科)的重要转变.
那么,毕达哥拉斯本人对于以他的名字命名的这个重要定理的证明究竟是怎样的呢?对此存在许多猜想,但一般都认为最初的证明是分割型的,像下面介绍的这样:设a,b,c分别表示给定的直角三角形的三条边,考虑图6-1(4)和图6-1(5)中的两个大的正方形,边长都是a+b,图6-1(4)把大正方形分成六个部分,图6-1(5)把大正方形分成五个部分,毕达哥拉斯从“等量减等量差相等”出发,便可推出左边图6-1(4)两个小正方形面积之和等于图6-1(5)中间正方形的面积,即a2+b2=c2.
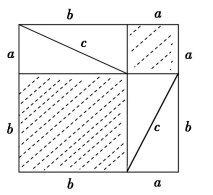
图6-1(4)
也许同学们会想,从图6-1(5)中利用 不是马上可以推出a2+b2=c2吗?但请注意,首先,在古代并没有我们现在看来很简单的这种代数运算,更为重要的是,毕达哥拉斯在这个证明中,他还必须证明由四个直角三角形拼出的图6-1(5)的中央部分的确是一个边长为c的正方形,为此,他还需要借助三角形内角和等于两个直角,而要想证明这个一般事实又需要知道平行线的某些性质,所以包括平行线理论在内的一系列很多初等几何理论的发展都应归功于早期的毕达哥拉斯学派.而这正是毕达哥拉斯学派的贡献.在毕达哥拉斯的“证明”思想影响下,后期的欧几里得将他的“逻辑演绎理论体系”推到登峰造极的高度.
不是马上可以推出a2+b2=c2吗?但请注意,首先,在古代并没有我们现在看来很简单的这种代数运算,更为重要的是,毕达哥拉斯在这个证明中,他还必须证明由四个直角三角形拼出的图6-1(5)的中央部分的确是一个边长为c的正方形,为此,他还需要借助三角形内角和等于两个直角,而要想证明这个一般事实又需要知道平行线的某些性质,所以包括平行线理论在内的一系列很多初等几何理论的发展都应归功于早期的毕达哥拉斯学派.而这正是毕达哥拉斯学派的贡献.在毕达哥拉斯的“证明”思想影响下,后期的欧几里得将他的“逻辑演绎理论体系”推到登峰造极的高度.
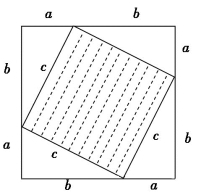
图6-1(5)
毕达哥拉斯根据这个定理画了一个可以无限重复的图形(如图6-1(6)).重复数次后的形状好似一棵树,所以被称为毕达哥拉斯树.
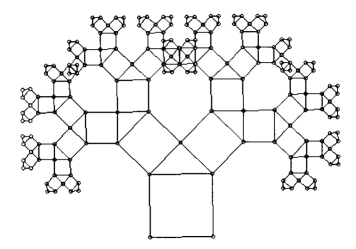
图6-1(6)
我们可以通过改变不同形状的直角三角形来改变这棵树.
无限细分,一直重复下去,这棵树枝繁叶茂(如图6-1(7)).
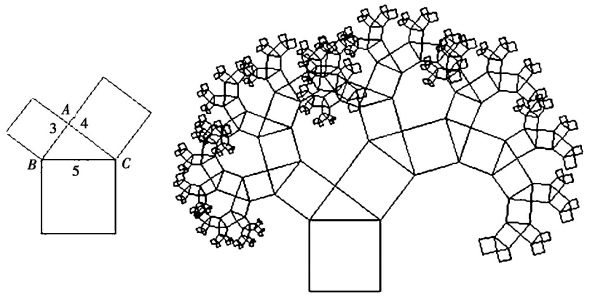
图6-1(7)
a2+b2=c2原来可以这么美!
相关文章

这是毕达哥拉斯纪念碑,碑体呈直角三角形形状.毕达哥拉斯是古希腊哲学家、数学家,创建了宗教、政治、学术合一的著名的毕达哥拉斯学派,该学派信奉“万物皆数”,发现了毕达哥拉斯定理,定义了奇数、偶数、完全数、亲和数等概念,研究了图形数的规律.知能概述用一个正整数b去除另一个正整数a,若商为q,余数为r,则有a=bq+r.余数有以下基本性质:b|(a-r);一个正整数a被另一个正整数n(n>1)除时,余数只可能是0,1,2,…......
2025-09-29

命题5.4.1设M、N两点在直线AB的同侧,则MN∥AB的充分必要条件是△MAB=△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q,若同位角相等,则AB∥CD。于是,共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中,有∠A=∠A′或∠A+∠A′=180°,则。命题5.4.5PQ∥AB,若直线l与AB垂直,则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2,而l3与l1、l2相截,则内错角相等。......
2025-09-30

学生:我曾在杂志上看到一篇文章,为了寻找外星文明,科学家向外太空发射的地球信息中,就有体现勾股定理内容的图案,文章说,这个图案代表数学和人类文明.如果有外星文明存在,那么他们一定能看懂这个“宇宙结构”所包含的意义.所以我认为勾股定理一定有它的奥秘.老师:哦,是这样.那么,我们今天就来讲讲勾股定理,如何?......
2025-09-30

如图6-14,在正△LMN内任取一点P,就有图6-14由P向MN、NL、LM分别作垂线,垂足为A、B、C,则有这里a=MN=NL=LM。对于任一个不同于P的点Q,因为“斜线比垂线长”,则有比较与得这表明P是与A、B、C距离之和最小的那个点。以下的论证,就是重复式到式了。如图6-19,若A、B、C、D不共线,不妨设C在△ABD的外接圆内或圆周上。利用AC′-CC′=AC及式得AC·BD≤BC·AD+CD·AB,其中等号仅当BC⊥A′D′......
2025-09-30

,xn是(a,b)内任意n个点,证明:ξ∈[a,b],使得证因为f在[a,b]上连续,且f≥0,故f在[a,b]上存在最大值M与最小值m,且M,m均大于或等于0,则由介值定理的推论可知,ξ∈[a,b],使得......
2025-09-30

图5-7[例5.3.1]如图5-7,四边形ABCD的对角线AC、BD交于M。[例5.3.2]如图5-8,△ABC的两中线AD、BE交于M,求证:AM=2MD。求证:图5-9证明:由共边定理[例5.3.4]在例题5.3.3条件下,求证:证明:由共边定理三式相乘,即得[例5.3.5]如图5-10,在△ABC的两边AB、AC上分别取两点P、Q。[例5.3.7]如图5-12,在△ABC的3边上分别取3点D、E、F,使BD=λCD,CE=μAE,AF=ρBF。......
2025-09-30

考点:二项式定理(2x+)5的展开式中,x3的系数是___________.1.在(2+x)6的展开式中,x5的系数是___________.2.若(x+) 10的展开式中x6的系数为30,则a=________.3.在7的展开式中,x2的系数为___________.4.设a=d x,则二项式()6的展开式中常数项是___________.5.已知(x-1)6展开式中含x2项的系数为0,则正实数a=________.6.设(1-x)5=a0+a1x+a2x2+…......
2025-09-30

所謂“甲骨”本是“龜甲獸骨”的簡稱。由研究甲骨文字而成立的學問,稱爲“甲骨學”。使甲骨學由文字的校訂推進到古史的考證的,是王國維。此外研究甲骨而比較地有成績的,是葉玉森,郭沫若。甲骨文字當然也逃不了這命,起初只是偶然的發現,並不是有計劃的發掘。以上所談,不過是甲骨的發現和甲骨學演進的小史,現在且進一步,談談甲骨學對學術的關係。中國學問最先受到甲骨學的影響的是文字學。......
2025-09-30
相关推荐