所有科学的发展都以一条假设为基础：宇宙在以一种可以为人类所理解的方式运转.在纷繁多彩、令人诱惑的自然现象背后，隐藏着某种简洁的规律，人类思维能与这种规律协调相符，多亏有了数学，人类正是通过数学来研究探索宇宙运行的基本法则.数学是科学发展的基石.在许多同学们的眼里，阿基米德、牛顿是以物理学家的形象出现的，殊不知他们还是最杰出的数学家.今天我向大家再重点介绍一个人物，他也是一位物理学家，但他同时也应该......
2023-11-19
被遗忘的数学课：一场不合逻辑发展的授课
【摘要】：为帮助青年教师成长，数学组开展“结对子”活动，我算是属于“经验丰富”之列，青年教师A跟我学，拜我为师.高一数学新增了向量内容，A要求听一堂课，按教学计划下一堂课应该是《向量的数量积的坐标表示》，我认真做了准备，新课将由常规的“复习式”引入.“同学们，关于向量的运算，我们从几何上定义了向量的加法和减法，研究了向量加法和减法的运算律，然后通过向量的坐标表示，用数量运算取代向量加减的几何运算.前几节课我
为帮助青年教师成长，数学组开展“结对子”活动，我算是属于“经验丰富”之列，青年教师A跟我学，拜我为师.
高一数学新增了向量内容，A要求听一堂课，按教学计划下一堂课应该是《向量的数量积的坐标表示》，我认真做了准备，新课将由常规的“复习式”引入.
“同学们，关于向量的运算，我们从几何上定义了向量的加法和减法，研究了向量加法和减法的运算律，然后通过向量的坐标表示，用数量运算取代向量加减的几何运算.前几节课我们从物理上“功”这个概念出发定义了向量的一种乘法，研究了向量乘法（数量积）的运算律，今天我们应该学习什么？”
为了顺利地进入新课内容，边说我边在黑板上写上了：
我请同学生1回答，如果她认真听了我刚才的“导引”或稍微进行了一点预习，都将顺利地进入新课内容.
生1：“前面我们已经学习了向量的加法、减法和乘法，我想，这节课我们应该学习向量的除法.”
她的回答完全出乎我的意料，下面也有个别同学在抿嘴发笑，我看了生1一眼，脸上隐约露出不悦的神色，内心在怪她没有顺着我的思路导入课题，我叫了刚刚在笑的一位同学生2.
生2：“今天我们应该学习向量的数量积的坐标表示，用数量的运算取代向量的运算.”
生2流利地导入课题，向四周看了看，很得意的样子.
“坐下！”
我转过身在黑板上写上课题《§9.2向量的数量积的坐标表示》，回过头来，却看见生1仍站在那里，低着头，满脸通红.
为了缓和一下她的情绪，我对生1说：“前面我们学习了向量的加法、减法和乘法，接下来学习向量的除法，这个思路也有一定的道理，请大家打开课本，看教材中有没有向量的除法.”
教室里出现哗哗翻书声，青年教师A也坐在那里查找.
“没有.”“没有.”
“为什么没有？”话一出口，我就觉得不妙了，这一问实在太随意了.怎么收场？5分钟过去了，还没有切入正题呢.
“为什么没有向量的除法？”学生们有的似乎在思考，大部分在望着我，怎么办？敷衍两句，强行进入课题总有点不太好，我在教室里踱着方步，脑子里在飞速地思考，因为平时根本就没有考虑过这个问题，心中无数，但现在必须面对这个问题，我继续在教室里踱着方步，一边望了望A，A回敬地望了我一眼，我想他在等待.
“碰！”生3举手要求发言，右手磕在桌子上咚咚作响.
生3：“除法就是乘法！除法是乘法的逆运算，课本只要把乘法讲清楚了，除法可以转化为乘法，所以我认为没有必要再单独来讲向量的除法.”
下面出现笑的声音，讨论的声音，让很多同学的心情都放松了，望着我表情很丰富的样子，生3显然混淆了向量运算与数量运算的关系，这堂课怎么办？看样子只有豁出去了，顺其自然地发展吧.
“请大家回忆一下，向量减法是在向量加法的基础上定义的吗？”(www.chuimin.cn)
生3：“是通过定义一个向量的‘相反向量’来实现的.”
“如果按这个思路，要把向量的除法变向量的乘法，需要什么基础？”
生3：“需要定义一个向量的‘倒向量’，就像一个数的倒数一样.”
“好，请大家考虑一下，已知一个向量a，如何定义a的倒向量？”
几分钟过去了，没有人回答这个问题，我点了科代表生4回答.
生4：“我不知道
是个什么东西.相反向量的意义很好懂，它仍是一个向量，它的模和方向与原向量的关系很明确，
是一个向量？还是一个数值？假设是一个向量，它的模与原向量的模互为倒数，但方向呢？”
“回答得很好！同学们，向量与数量是两个不同的概念，他们既相似又有很大的不同，千万不能把向量的概念与数的概念等同起来，所以生3的想法有道理又没有道理.其实向量的乘法只是我们习惯上的一种叫法，我们指的是向量的数量积.”
生5：“我觉得可以定义a的倒向量，它的模是a的模的倒数，方向取与a的垂直方向.”
生4：“我认为不行，假设这样定义，两个向量的除法是可以转化为乘法，但将导致任意两个非零向量相除（数量商）的结果为0，这没有什么意义.”
“教材中没有向量的‘数量商’，是中学阶段不学吗？不是，将来大学阶段也不会学，因为目前数学界还没有给出向量除法的定义，当然大家完全可以想一想，看是否可以由我们来定义呢？谁合理地定义了向量的一种除法，说不定还会在数学史上留有一席之地呢！”我已完全放松，一边幽默地说着，脑子里也在飞快地想着这个问题.
“要想定义向量的除法，先要考察向量的乘法，从向量的数量积的定义方法中去寻找思路.”
下面有的在翻书，有的在比画，有的在讨论.
生6：“我觉得可以定义.教材中从力做功的模型上定义了向量的数量积，使我想到牛顿第二定律，假设运动物体在力F的作用下产生加速度a，力F与加速度a夹角为θ，则有Fcosθ=ma，那么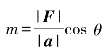
，所以两个向量的“数量商”等于两个向量的模的商与两个向量夹角的余弦值的积！数量积的意义是“功”，“数量商”的意义是‘物体的质量’，它们都是数量！”
生6俨然一匹黑马，为自己绝妙的想法洋洋得意，神采奕奕，没想到学生这么快就有了发现，我为学生的“发现”而惊叹！正想发表一些评论，下课铃响了.
“同学们回去再想想，看如何定义两个向量的数量商合理，生6的想法很好，请大家注意，虽然“定义”是人为规定的，但要考虑你的定义是否合理，是否有应用效果，否则就没有生命力，还要注意在整个数学体系中你的定义是否会带来逻辑矛盾，这些都要做进一步的思考与研究.建议同学们课后再考虑一下，以后我们有机会再一起讨论.”
生5强烈要求发言.
生5：“按照我前面的思路，向量a的倒向量
仍是一个向量，定义它的模是a的模的倒数，方向与a垂直，这样两个向量的‘数量商’是两个向量的模的商与两向量夹角的余弦值的积.与生6的结论异曲同工，完全一致，但我发言在先，应该拥有这个发现的优先权.”
教室里充满了爽朗的笑声.
回到办公室，我同A交换了意见.我们一致的看法是这堂课有点意思，感到我们的学生的创造潜能很大，但有两个问题：一个是我建议A在他班上也用一节课时间来进行讨论，A担心他教的普通班学生素质不如重点班，怕学生讨论不起来，课上不下去；另一个是下一节课我是继续讨论“数量商”的问题并就我们的牛顿与莱布尼茨优先权之争进行裁决，还是开始讲授我的“向量数量积的坐标表示”呢？
有关被遗忘的数学课的文章
- 详细阅读
-
揭开虚数的奥秘：被遗忘的数学课详细阅读
前几年浙江卫视《一周立波秀》节目作为中国的脱口秀名噪一时，很受欢迎，其中有一期节目谈到学校教育.我们小学数学的很多应用题中的主人公都叫小明，什么抽水问题、相遇问题、盐酸和水倒来倒去的问题，很是头疼，把小明都要弄成神经衰弱了，不知可怜的小明现在怎么样了，等到我们读初中，知道那些问题都可用方程来解，似乎一下子可控制住了，初中老师经常会说“世界上的任何问题都是数学问题，任何数学问题都是方程问题”，以此来......
2023-11-19
-
年轻人玩数学：被遗忘的数学课详细阅读
哈代在其著名的《一个数学家的辩白》中写道：“年轻人应该证明定理，而老年人则应该写书，任何数学家都永远不要忘记：数学，较之别的艺术或科学，更是年轻人的游戏，举一个简单的例子，在英国皇家学会会员中，数学家的平均当选年龄是最低的.”数学很大程度上是年轻人的科目，它是智力的竞争，只有年轻和才气旺盛才能充分满足它的要求，同昔日的体坛英雄一样，许多才华横溢的年轻数学家，在写出一两篇有前途的论文后便湮没于世.拉......
2023-11-19
-
被遗忘的数学课：微积分的奥秘与应用详细阅读
在上一次的讲座中，我们回顾了积分和微分概念的产生和建立的过程，随着笛卡儿、费马解析几何的创立，我们可以把先辈们苦心得来的一些零星的发现，把形形色色的求积问题，统一归结到在坐标系平面内求曲线f（x）下的面积，从而建立了函数积分的概念；我们用平均速度逼近瞬时速度，用割线逼近切线，抽象出一种用平均变化率逼近瞬时变化率的方法，定义了函数的微分（导数）.但光有这些我们还无法真正了解微分和积分的奥秘和它们作为......
2023-11-19
-
数论研究的前奏，来自《被遗忘的数学课》详细阅读
对我们每个人来说，数学都是从算术开始的，算术研究的是最基本的数量概念，即整数1，2，3……谈到最普通的数学思想，区分个体数目的思想，那就是计数.“上帝创造了整数，其他一切都是人制造的”，德国数学家克罗内克这句著名论述，揭示了整数内在的必然性以及它们无可否认的自然性，无论数学发展到什么阶段，整数总是根基.数学家称这些无穷无尽的1，2，3……......
2023-11-19
-
被遗忘的数学课：微分和积分的意义和发展详细阅读
“微分”，“微”是“细微、微小”的意思，而“分”的意义是“细分、分割”，微分，就是通过观察事物微小变化或瞬间特征来把握事物整体的一种方法.积分的萌芽和产生可以追溯到久远的年代，起源于面积的计算（而后扩展到体积和弧长），在运动、变量进入数学之前，积分实际上是一种静态的、孤立的计算技巧（这个技巧就是前面我们讲的分割求和的方法），而微分的兴起则是17世纪以后的事情.随着欧洲文艺复兴运动的蓬勃发展，物理学......
2023-11-19
-
纯数学与应用数学：被遗忘的数学课详细阅读
对某一学科或某一事物，人们常常用“分类”思想来进行把握和认识，仅仅就解题而言，我们知道“分类讨论”通常也是一种重要的解题手段，对我们普通的中学生而言，数学是什么？......
2023-11-19
- 详细阅读
相关推荐