拉马努金的天才信件引爆全球关注

2023-11-19 理论教育版权反馈

【摘要】：哈代邀请好友李牧尔伍德一起共同审视拉马努金的信件，他们得出结论，这绝对是一个数学天才的杰作，就这样，贫穷的拉马努金只身前往英国，开始了被伟大的哈代称为“自己一生中最重要的合作”.“另一个故事的主人公大家都很熟悉，他就是大名鼎鼎的爱因斯坦，爱因斯坦创立的相对论的意义不仅仅在物理界，可以这样说，相对论的思想更大的意义在哲学上，这为他赢得了巨大的声誉，由于相对论是爱因

高一下学期期末综合测试卷中有一道选择题：在△ABC中，

（1）若sin2A=sin2B，则△ABC为等腰三角形；

（2）若sin2A=cos2B，则△ABC为直角三角形；

（3）若cos（B-C）·cos（C-A）·cos（A-B）=1，则△ABC为等边三角形；

（4）若sin2A+sin2B+sin2C＜2，则△ABC为钝角三角形.

以上四个命题中，真命题的个数是（　）.

A.0　B.1　C.2　D.3

这是一道中档题，改卷时发现大部分同学都选对了，我自己在思考这道题时，感到命题（4）有点文章可做，于是在讲评试卷时想对学生的解题思路进行一番考察.

因为这是一道小题，而且大部分同学都选择对了，所以学生颇“不以为意”，我点了一个成绩一般的同学（生1）来回答.

生1：“我用一个特殊的钝角三角形试了一下，令A=120°，B=C=30°，sin2A+验证成立.”

我一边听一边微笑地望着她点了点头，并没有让她坐下的意思，可她赶紧坐下去了，逃之夭夭.

下面开始出现轻微的讨论的声音，我让另一位同学（生2）继续.

生2：“我除了用120°，30°，30°尝试外，还选了150°，15°，15°，计算上稍微复杂一点，两次验证都没什么问题，但我心中还没有底，想从sin2A+sin2B+sin2C＜2出发进行推理，可是没推出来.”

生1，生2的想法完全在我的意料之中，我用眼光扫了一眼，议论的学生多了一些.生3的神情告诉我，他有新想法.

生3：“选择题的要求是准和快，这道题从条件推出钝角三角形不大好办，我是这样考虑的，当△ABC是直角三角形时，显然sin2A+sin2B+sin2C=sin2A+sin2（90°-A）+sin290°=2.当△ABC是锐角三角形时，我用等边三角形验证：sin2A；这时我就感觉到对于钝角三角形应该是sin2A+sin2B+sin2C＜2，命题应该是正确的，再用120°，30°，30°试了一下也没有什么问题，于是我就判定该命题是真命题.”

生4是副班长，是一位自信、好学、成绩扎实的学生，看到我还在这里纠缠，似乎有些不耐烦.

生4：“这个命题的判断，严格来说不能用验证法来解，应该从条件出发进行推理论证.”

我示意生4上台板书.

板书：因为sin2A+sin2B+sin2C＜2，

所以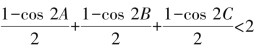 pagenumber_ebook=90,pagenumber_book=82 .

整理得cos2A+cos2B+cos2C+1＞0，

即2cos（A+B）cos（A-B）+2cos2C＞0，

即cosC·[cosC-cos（A-B）]＞0，

即cosC·[cos（A+B）+cos（A-B）]＜0，

所以cosA·cosB·cosC＜0.

因为△ABC中至多只有一个钝角，

所以cosA，cosB，cosC中有且只有一个值小于零，

所以△ABC是钝角三角形.

（漂亮！）生4很得意地回到座位上.(www.chuimin.cn)

大家为生4的演绎推理所折服.这道题到此为止吧.学生纷纷准备听我讲评下一题，我看时机成熟，认真地对大家说：“生4的证法无懈可击！但我有话要说.”

学生的思想被重新拉回到这道题上面，生4满脸疑惑.

“我认为生3的判断思路很好！简洁，有新意！”学生纷纷向生3投去羡慕的目光.

生4：“生3和生2的方法都不严密，好像不大保险.”

生3意外地得到老师的表扬，喜悦之情溢于言表：“我和生2的判断方法是不同的，生2是从内部验证，而我却是从外部推理的.”

生4虽然觉得生3有点道理，但显然不服气.“请问，生3的推理的依据是什么？”

生3无以言对，但坚信自己是对的，他用眼睛望着我，寻求支持，这时，我转身在黑板上写上：

前提：直角三角形满足sin2A+sin2B+sin2C=2，

锐角三角形满足sin2A+sin2B+sin2C＞2，

结论：钝角三角形满足sin2A+sin2B+sin2C＜2.

推理依据：数学内在的和谐性！

这可是个新鲜、大胆的想法，有意思，所有学生都在议论，有的冲我点头微笑，好像感悟到了点什么.

生4因为自己“正宗”的解法被忽视，一时似乎还转不过弯来.

生4：“老师，请问‘数学是和谐的’能作为推理的依据吗？”

我的意图是通过这道小题让学生体会一下“数学是和谐的，数学是美的”这个概念，以使学生更好地认识数学、理解数学，同时培养学生的数学直觉，看来，让学生接受这个概念要比接受“数学是抽象的，数学是逻辑的”困难得多.

“同学们，生4的问题提得很好，‘数学是和谐的，数学是美的’这个概念很重要，今后的数学学习中，我们还会有更多的体会，当然，这不能成为推理的依据，为使大家体会到我的意思，下面我给大家讲两个故事.”

数学课有故事听，所有的学生都放松了思想，显得很兴奋，一个个准备听故事的样子，教室里安静了许多.

“印度是一个文明古国，也是一个神秘的国度，19世纪，印度有一个真正的数学天才，他的名字叫拉马努金，由于家境贫寒，他从未受过正规的数学教育，但这位孤立的年轻人却在从事着极富独创力.极有深度的数学研究，为了使自己有更好的发展，1913年，他把自己的研究成果分别寄给英国的三位数学家，其中两位大人物因为显然‘还有比给一个不知名的印度小职员回信更重要的事情要做’.拉马努金的稿件他们看都没看便被退了回去.”

第三位数学家是剑桥大学的G.H.哈代，本来他或许也会这样做，拉马努金用蹩脚英文写的信中有100多个奇怪的公式，诸如

拉马努金（印度，1887—1920）

哈代（英国，1877—1947）

没有任何证明，仿佛一个妄想狂随心所欲地漫游世界，哈代随手把信丢在一旁.

但是，这些数学公式一整天萦绕在他的脑海中，哈代辨识出某些公式已为人所知，但是其他许多公式则显得奇特，不知从何而来，逐渐地，哈代醒悟了，认识到这些公式“一定是真实的，因为如果它们不真实，就不会有人能有这样的想象力，发明出它们来！”哈代邀请好友李牧尔伍德一起共同审视拉马努金的信件，他们得出结论，这绝对是一个数学天才的杰作，就这样，贫穷的拉马努金只身前往英国，开始了被伟大的哈代称为“自己一生中最重要的合作”.

“另一个故事的主人公大家都很熟悉，他就是大名鼎鼎的爱因斯坦，爱因斯坦创立的相对论的意义不仅仅在物理界，可以这样说，相对论的思想更大的意义在哲学上，这为他赢得了巨大的声誉，由于相对论是爱因斯坦通过‘思维实验’推测出来的，它太深奥了，据说当时世界上只有三个学者真正懂得相对论思想，在这里，理论上的推测走在实验证明的前面去了，1918年，著名的英国天文学家和物理学家爱丁顿组织了一支科学考察队，兵分两路，一支去几内亚湾的普林西比岛，另一支去巴西的索不拉尔偏僻的农村，开始了对相对论的命运有非常重大影响的考察验证.考察队出发前有记者担心地问爱因斯坦：‘若考察的结果与您的相对论理论不符，您将怎么看？’爱因斯坦坚信自己的理论具有崇高的和不容争辩的‘内在的完备’，他笑着回答说：‘那将是上帝的错误，我将感到非常遗憾.不过记者先生，您的担心是多余的，因为宇宙的设计是和谐的！’一年以后，爱丁顿率科学考察队回到英国，请问同学们，他是证实了还是否定了爱因斯坦的理论？”

“证实了！”同学们都轻松地笑着回答.

“不错！科学考察证实了相对论的理论是正确的，它只能是正确的，请问生4为什么？”

生4：“因为宇宙的设计是和谐的！”

我带头为生4鼓起掌！

拉马努金的天才信件引爆全球关注

相关推荐