佛教养正院已办有四年了。好像还没有,因为我尚有一线天良常常想念自己的过失。可是到了今年,比去年更不像样子了;自从正月二十到泉州,这两个月之中,弄得不知所云。尤其是今年几个月之中,极力冒充善知识,实在是太为佛门丢脸。只有对于养正院诸位同学,相处四年之久,有点不能忘情;我很盼望养正院从此以后,能够复兴起来,为全国模范的僧学院。......
2024-01-28
前面我们从历史的长河中撷取两个片段,使我们对e的起源的认识有了长足的进步,e终于不再抽象了.但要更多地认识e的奥秘,更深入地了解它的魅力,我们还要继续向前迈进,进入数学的圣地,那就是微积分!
牛顿和莱布尼兹在发展微积分学时,主要把微积分应用于代数曲线,也就是方程为多项式或多项式之比的曲线,这些方程很简单,实际应用中也有很多这样的方程(如抛物线y=x2和双曲线![]() 就是两个简单的例子),但人们在应用中发现,很多曲线并不属于代数曲线,而是超越曲线(这一术语是由莱布尼兹创造的,表示曲线的方程超过了初等代数学的研究范围),其中声名最为显赫的当数指数曲线.
就是两个简单的例子),但人们在应用中发现,很多曲线并不属于代数曲线,而是超越曲线(这一术语是由莱布尼兹创造的,表示曲线的方程超过了初等代数学的研究范围),其中声名最为显赫的当数指数曲线.
指数函数y=ax(a>0且a≠1)的变化率是非常令人震惊的.图3-3(1)所示的是所有指数曲线的一种情形,不管它的底数是什么,而这一图形的简洁性也是一目了然的.它缺乏一个代数函数应当具备的大部分特征:例如x轴的截点(图形与x轴的交点)、最大值点、最小值点和拐点,初看起来,指数函数图象如此简单、无味,但它有一个非常重要的特点,那就是它的变化率(导数).
问题:求指数函数y=ax(a>0且a≠1)的导数.
根据导数的定义,我们有:
![]()
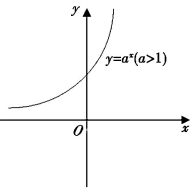
图3-3(1)
为了方便起见,我们将符号Δx用一个简单的字母h代替,因此等式(1)可变为

我们可以将因子ax从极限运算中移出,因为等式(2)中的极限运算涉及的变量是h,x这时被看作常量.因此,我们得到如下的表达式

我们将极限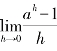 的值用字母k来表示,那么就得到如下的结果:
的值用字母k来表示,那么就得到如下的结果:
若y=ax,则
![]()
这一结果非常重要,它表明:指数函数的导数与它自身成比例.
请大家注意,到目前为止,a(a>0且a≠1)的选择完全是任意的.
人们自然会想到:能否找到某个特定的a,使结果特别简练呢?若能选择一个合适的a,使得比例常数k恰好等于1,显然可以使得等式(4)变得最为简单.如果是这样,那将是底数a的最“自然”的选择.
这里,我们从假定h为有限数时开始,令表达式![]() ,解出a可得a=
,解出a可得a=![]() ,我们再回过头来令h→0,得到
,我们再回过头来令h→0,得到![]() ,将等式中的
,将等式中的![]() 用字母m代替,那么h→0也就意味着m→+∞,因此我们有
用字母m代替,那么h→0也就意味着m→+∞,因此我们有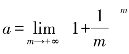 ,这是我们熟悉的一个东西,这个极限值正是我们神圣的数字e,至此,我们得到如下的重要结论:如果选择数字e为底,那么指数函数的导数等于它自身,用符号表示就是
,这是我们熟悉的一个东西,这个极限值正是我们神圣的数字e,至此,我们得到如下的重要结论:如果选择数字e为底,那么指数函数的导数等于它自身,用符号表示就是
如果y=ex,那么
![]()
值得特别强调的是,函数ex的微分(积分)不变的特性,是任何其他函数都不具备的,函数ex被称为自然指数函数,它在数学和科学中的核心角色是如下事实的直接结果:人们发现,在一些现象中,如果某些变量的变化率(微分)与它本身成比例,那么任何一个此类的现象都可以抽象为微分方程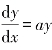 y(特殊情况:若a=1,则微分方程为
y(特殊情况:若a=1,则微分方程为![]() ,我们得到的一般解为y=cex,其中c是任意常数,这一解所代表的不是一个函数,而是一个指数函数的家族,其中每一个不同的c值都对应一个不同的函数);若a≠1,则微分方程
,我们得到的一般解为y=cex,其中c是任意常数,这一解所代表的不是一个函数,而是一个指数函数的家族,其中每一个不同的c值都对应一个不同的函数);若a≠1,则微分方程![]() 的解为y=ceax,(其中常数c可由系统的初始条件决定).这个微分方程在放射性物质的衰变、声波在空气中的传播、物体的冷却、人口的增长等广泛领域都发挥着至关重要的作用.
的解为y=ceax,(其中常数c可由系统的初始条件决定).这个微分方程在放射性物质的衰变、声波在空气中的传播、物体的冷却、人口的增长等广泛领域都发挥着至关重要的作用.
有了微积分这个有力的数学工具,更有助于我们对e的了解.通过考察指数函数和对数函数的导数,我们无疑会进一步明确选择“自然底”的优越性.
例1:求y=logax的导数(a>0且a≠1).

所以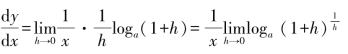
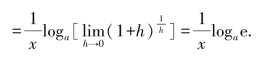
若取e为底,则有![]() ,也就是
,也就是![]() ,非常简单.
,非常简单.
例2:利用导数求e的近似值.
欧拉认为,一切连续函数均可展开为无穷级数,指数函数y=ex可展开为如下的无穷级数:
ex=a0+a1x+a2x2+…+anxn+….
令x=0,得a0=1,
因为ex的微分形式不变,所以
(ex)′=a1+2a2x+3a3x2+…=ex,
令x=0,得a1=1.
(ex)″=2a2+3×2a3x+4×3a4x2+…=ex,(www.chuimin.cn)
令x=0,得![]() .
.
(ex)‴=3×2a3+4×3×2a4x+…=ex,
令x=0,得3×2a3=1,即![]() .
.
ex微分多少次都依然不变,真是不可思议的函数.由此我们循环计算可得:
![]()
据此,![]() ,
,
令x=1,可得![]() .
.
前面我们通过二次展开也可得这一结果,这一级数表达式可以快速地计算出e的值.
至此,我们大致知道了e,e之所以被冠以“自然之数”,一方面,就像“自然数”是人们在计数过程中自然而然产生的数一样,人们在研究对数和对数函数的时候,发现以e为底会使问题变得最为简洁,以e为底是一种“自然”的选择,另一方面,e是增长的极限,它体现了宇宙的形成、发展及衰亡的“大自然”的本质规律.
最后,让我们再撷取几个片段,一起来欣赏e.
1.如果说,数学是自然科学的皇后,而数论是皇后头上的皇冠,那么素数就是皇冠上的宝石.对素数的研究作为纯数学的极致,几千年来一直是顶级数学家和业余数学家的最爱,公元1830年,高斯天才地发现小于N的素数的个数π(N)与e有关.当N充分大时,![]() (法国数学家勒让德(1752—1833)也独立地发现了这一猜想).1896年,这一猜想被法国数学家阿达玛和比利时数学家普森同时独立地严格证明,由于这一定理在数论研究中的重要性,数学家把这一定理称为“素数定理”!
(法国数学家勒让德(1752—1833)也独立地发现了这一猜想).1896年,这一猜想被法国数学家阿达玛和比利时数学家普森同时独立地严格证明,由于这一定理在数论研究中的重要性,数学家把这一定理称为“素数定理”!
2.前苏联著名科普作家雅·伊·别莱利曼在《趣味代数学》里,曾提到过这样一个有趣的问题:“已知数a,把它分成若干部分,如果各部分乘积要最大,应该怎样分?”我们知道,由定和求积原理,当几个数的和不变时,要想乘积最大,务必使各个数都相等,如果数a分成相等的若干部分,那么究竟要分成几个部分呢?鬼使神差的是,可以证明,当每个部分跟数e最接近时,各部分的连乘积一定最大.
例如,若a=20,按计算,最接近![]() 的整数是7,也就是说要把20七等分,我们可从以下表中看得一清二楚.
的整数是7,也就是说要把20七等分,我们可从以下表中看得一清二楚.
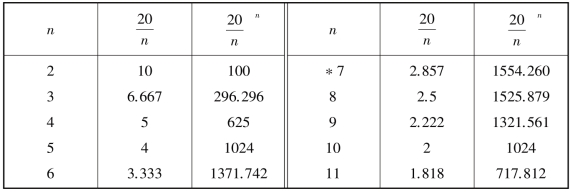
将20分成7等分,每个数都为2.857,这时积1554.260最大.
3.由于ex的微分不变性,不管对它微分多少次它永远还是ex,如今大学校园里,恋爱之风盛行,数学系的学生通常会用e比喻坚定不移的爱情:“微你千遍也不变,牵手的日子在永远.”
4.欧拉选择用e表示![]() 的极限值的理由有二:一个理由是在a,b,c,d等四个经常被使用的字母后面,第一个还没有被经常使用的字母就是e,所以他自然地选择了这个符号,另一个理由是虽然欧拉是瑞士人,但当时常用的英文、法文、德文中,“指数”一词的第一个字母都是e,而欧拉认为对数源出于指数,所以欧拉选择了e.而传说欧拉用自己的名字Euler的头一个字母命名是没有根据的,因为欧拉是一位非常谦逊的人,他经常推迟他自己成果的发表以帮助他的同僚或学生的工作得到应有的认可.不管因何原因,和他所选择的其他字符一样,字符e已被人们广泛接受了.
的极限值的理由有二:一个理由是在a,b,c,d等四个经常被使用的字母后面,第一个还没有被经常使用的字母就是e,所以他自然地选择了这个符号,另一个理由是虽然欧拉是瑞士人,但当时常用的英文、法文、德文中,“指数”一词的第一个字母都是e,而欧拉认为对数源出于指数,所以欧拉选择了e.而传说欧拉用自己的名字Euler的头一个字母命名是没有根据的,因为欧拉是一位非常谦逊的人,他经常推迟他自己成果的发表以帮助他的同僚或学生的工作得到应有的认可.不管因何原因,和他所选择的其他字符一样,字符e已被人们广泛接受了.
5.数字e的几何意义:指数函数y=ex,当x∈(-∞,1)时,曲线y=ex与x轴构成的区域面积等于e,即![]() (如图3-3(2));
(如图3-3(2));

图3-3(2)
指数函数y=ex在点(1,e)处的切线的斜率为e.
6.一些与e有关的奇妙的数:
![]() ,这是表达式
,这是表达式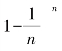 在n→+∞时的极限值,这个数常用来计算指数函数y=e-ax衰减的速率;
在n→+∞时的极限值,这个数常用来计算指数函数y=e-ax衰减的速率;
ln2=0.693147181…,它是正负交替的调和级数![]() 的极限值.
的极限值.
7.神奇的螺线由e来把控(如图3-3(3),3-3(4)):
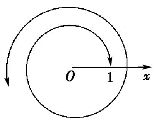
图3-3(3)
r=eaθ(a>0)
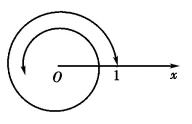
图3-3(4)
r=e-aθ(a>0)
8.连分数:连分数在表示一个无理数时,有时会描述出无理数的一些“规律性”特征,如:

9.莫泊桑的小说《项链》描述的故事大家都很熟悉,项链戴在脖子上,自然地悬在那,这产生了数字上著名的“悬链问题”.这条悬链曲线其实不是抛物线,它的方程是![]() .
.
有关被遗忘的数学课的文章

佛教养正院已办有四年了。好像还没有,因为我尚有一线天良常常想念自己的过失。可是到了今年,比去年更不像样子了;自从正月二十到泉州,这两个月之中,弄得不知所云。尤其是今年几个月之中,极力冒充善知识,实在是太为佛门丢脸。只有对于养正院诸位同学,相处四年之久,有点不能忘情;我很盼望养正院从此以后,能够复兴起来,为全国模范的僧学院。......
2024-01-28

“无穷小”是微分和积分的关键,无论是求瞬时速度,还是求曲线图形的面积,两者的共同点,或是将时间幅度或是将长方形的宽度无限缩小,无穷小不可避免的同时既是0又不是0.小时候我们就曾被诸如0.999…......
2023-11-19

完全由基因决定的疾病称为单基因遗传病,此类疾病由特定的基因突变引起。目前已确定了数千种由这种单基因突变导致的疾病,而且每年还不断发现新的病种。尽管单基因遗传病的病种很多,但由于发生率较低,因此总体患病人数所占比例较小。因此,医学上对基因决定的疾病主要着眼于预防,这也是“优生优育”研究领域的主要任务之一。基因决定的疾病,致病基因存在于全身每一个细胞中,要用药物去攻击它非常困难。......
2023-11-03

在上一次的讲座中,我们回顾了积分和微分概念的产生和建立的过程,随着笛卡儿、费马解析几何的创立,我们可以把先辈们苦心得来的一些零星的发现,把形形色色的求积问题,统一归结到在坐标系平面内求曲线f(x)下的面积,从而建立了函数积分的概念;我们用平均速度逼近瞬时速度,用割线逼近切线,抽象出一种用平均变化率逼近瞬时变化率的方法,定义了函数的微分(导数).但光有这些我们还无法真正了解微分和积分的奥秘和它们作为......
2023-11-19

前几年浙江卫视《一周立波秀》节目作为中国的脱口秀名噪一时,很受欢迎,其中有一期节目谈到学校教育.我们小学数学的很多应用题中的主人公都叫小明,什么抽水问题、相遇问题、盐酸和水倒来倒去的问题,很是头疼,把小明都要弄成神经衰弱了,不知可怜的小明现在怎么样了,等到我们读初中,知道那些问题都可用方程来解,似乎一下子可控制住了,初中老师经常会说“世界上的任何问题都是数学问题,任何数学问题都是方程问题”,以此来......
2023-11-19

血型的确定揭开“血”的奥秘血液是人体中非常重要的物质,它拥有着输送氧和各种营养物质的功能,为生命活动提供必须的营养物质。人胚第三个月,脾是主要的造血器官。出生后,肝、脾造血停止,骨髓负起造血的全部责任。其中O型血的历史最为悠久。AB血型的人继承了耐病的能力,他们的免疫系统能更好地抵抗细菌。如果再次输入RH阳性血液,即可导致溶血性输血反应。其他医生纷纷效仿,结果造成大量受血者死亡。......
2024-07-06

看人先看眼不管是在传统相学中,还是现代交际中,眼睛都具有十分重要的作用,认真观察对方的眼睛和眼神,的确可以看出许多许多东西。“三白眼”就是瞳仁比较小,眼白比较多,瞳仁靠近眼白的一边,它的周围有三个地方出现眼白,这种眼睛被称为是“三白眼”。“三白眼”的人,个性都比较强,而且有的时候强到六亲不认。......
2023-12-02

FBI在经过调查后,拘留了当地一位据称是字画界权威的人。在FBI对犯罪嫌疑人进行审讯的时候,他没有表现出丝毫的惊慌。一番审讯下来,FBI觉得很棘手,于是请来了一位专门研究犯罪心理的前辈,希望他能够打破犯罪嫌疑人的心理防线,查出真相。最终,在FBI的审讯下,犯罪嫌疑人承认了犯罪事实,供出了自己作案的过程。......
2023-12-05
相关推荐