如何选择底数a以确保更高精确度的logaN对数表？

2023-11-19 理论教育版权反馈

【摘要】：要造logaN的对数表，须满足两个条件：1.对数值能取较密集的值，比如logaN=0.000，0.001，0.002，0.003……底数a的选择要使a的这些幂容易计算，而且这些a的幂的间隔不能太大.因为间隔大了，就会有许多真数N查不到对数值.按照上述要求，我们来研究一下a取什么值比较有利.若a=10，则真数……则会有更高精确度的对数表.由此可知，应取形如的数为底，且n越大越精确.根据计算与推理，人们发现的值随着n的无限增大而越来越逼近一个数2.71828…

在科学史上很少有像对数的发明那样受到整个科学界狂热追捧的数学概念，伽利略曾凝望如下数表：

陷入沉思，归于沉寂……人们难以想象，对数的发明这一天才的创造来源于一个不大有名的人——苏格兰的约翰·纳皮尔.

16世纪至17世纪初，各领域的科学知识急速发展.数学、力学、航海、天文等突破古老教条的束缚，急剧地改变着人们的世界观.哥白尼的“日心说”在经过近一个世纪与教会的斗争后终于渐渐为人们所接受.1521年，麦哲伦的环球旅行宣告了游遍地球每个角落的崭新航海探险时代的到来，而在同一时期，意大利人伽利略正在奠定力学的基础，德国人开普勒创立了行星运动三大定律，从此彻底颠覆了中世纪的“地心说”.这些科学发展带来了庞大的数据计算问题，科学家们不得不花费大量宝贵的时间专注于这些烦琐的数字运算，他们迫切地需要一种新发明，能够将他们从这些烦琐的运算中解放出来.

相对于加法运算，乘法简直就是一个噩梦（除法就更不用说了），这种枯燥的运算花费的时间太长，如两个五位数的乘法需要进行25次一位数的相乘，还不包括必要的加法和进位.纳皮尔开始思考：“看起来，在数学实践中，最麻烦的莫过于大数字的乘法、除法、开平方和开立方，计算起来特别费事又伤脑筋，于是我开始构思有什么巧妙的方法可以解决这些问题.”（纳皮尔《奇妙的对数表的描述》）

最简单的、有点意思的是公式，可以把乘法运算变成乘方运算，我们只要编制一个平方表，乘法运算就算解决了.但乘方、乘法基本上是同一级运算，而且除法和开方运算还不能解决，所以这个方法意义不大.

我们无法知道纳皮尔开始是如何想到“对数”这一发明的，他显然对下面的公式非常熟悉：

这个公式及类似的cosA×cosB和sinA×cosB公式就是我们所熟知的积化和差公式，这一公式的意义体现在：两个三角函数的乘法可以用其他三角函数的和或差表示出来.而加减运算比乘除运算低一级，要简便得多，也许就是这个公式激发了纳皮尔的灵感.

与纳皮尔发明有关的另一个更为直接的因素可能与几何级数有关.为了形象地描述这个思想，我们以2为底做进一步的说明.下表给出了以2为底，从n=-3到12之间的整数幂所构成的几何级数（等比数列）.

假设我们要用32乘以128，在表中我们找到32和128相对应的“代表者”分别为5和7，二者之和为12，而反过来表中“代表者”为12的数对应着数4096，这就是我们想要的32×128的答案.若我们要计算512除以8，通过查表我们找到相对应的“代表者”分别为9和3，二者之差为6，反过来表中“代表者”为6的数对应着数64，这就是512÷8的答案.

这一规律的实质是：隐藏在幂运算法则am·an=am+n这一模式之中，假设我们有一个值，比如32758，显然，这个值介于104与105之间，纳皮尔意识到，在4和5之间，必然存在某一个值P，使得32758=10P成立，也就是说，任何一个数都可以是10的幂，既然10的幂相乘很简单（指数相加），而任何数又都可以表示成10的幂，这意味着任何数相乘都很简单.

一般地，如果我们能将任何正数写成某个固定值（现在称为底数）的幂，那么计算数的乘、除法就可以转换为计算它们的对数的加、减法，进一步，计算一个数的n次幂，等于将相同指数相加n次（即指数乘以n），而对于一个数开n次方则等价于指数除以n.简而言之，基本算术运算都可以降为比该运算次一级的运算，这样就大大降低数据运算的复杂度.

我们用现代语言把这种思想表述为：若ab=N（a＞0且a≠1），则b称为以a为底的N的对数，记为b=logaN，对数背后的主要思想表现在我们熟悉的一组公式中（以下公式中a＞0且a≠1，M＞0，N＞0）.

理论上的框架建立起来了，但离实用还有很多艰苦的工作要做，前提是要找到一个庞大到无所不包的数（不仅是如表中列的整数）的对数表，这个数表需要解决两个问题：一是能查到任意一个正数的对数，二是已知一个正数的对数值能查到原来的那个数，即“真数”.这时，底的选择就显得非常重要了，最容易想到的“底”显然是整数2和10，2是最简单的数，而10因为进制的原因，所以很优越.

现在让我们来考虑一下，到底以什么数为底造对数表最方便？

要造logaN的对数表，须满足两个条件：

1.对数值能取较密集的值，比如logaN=0.000，0.001，0.002，0.003……这样的数表涵盖的数足够密集，能保证由对数值查真数.

2.在1的条件下，此时N=a0.000，a0.001，a0.002，a0.003……底数a的选择要使a的这些幂容易计算，而且这些a的幂的间隔不能太大.因为间隔大了，就会有许多真数N查不到对数值.

按照上述要求，我们来研究一下a取什么值比较有利.

（1）若a=10，则真数……这些开方显然都不易计算（取a=2，3等也都不易计算）.

（2）若取a=101000，则真数N=1，10，100，1000……容易计算，但N的间隔太大，不能满足使用的需要，如查不到1到10之间，10到100之间，100到1000之间的数的对数.

（3）若取a=（1.001）1000，则真数N近似为N=1，1.001，1.002，1.003……既达到了容易计算，而且数与数的间隔足够密集，便于造表.（注意：当x很小时，（1+x）n≈1+nx）(www.chuimin.cn)

（4）若取a=（1.0001）10000或（1.00001）100000……则会有更高精确度的对数表.

由此可知，应取形如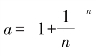 pagenumber_ebook=68,pagenumber_book=60 的数为底，且n越大越精确.根据计算与推理，人们发现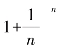的值随着n的无限增大而越来越逼近一个数2.71828…，人们把当n无限增大时的极限值用一个符号来表示：这就是e.

纳皮尔选择e为底，经过艰苦的计算，终于编制出了一个自然对数表.

至此，自然对数的底的神秘面纱已经揭开，对我们来说，e终于不再陌生了.

数学家布里格斯倾慕纳皮尔的奇妙的法则，为了与通行的数的进制相衔接，在纳皮尔的自然对数表的基础上，布里格斯与纳皮尔合作，共同编制了以10为底的对数表.这就是我们通常所说的常用对数表.他们用了近10年的时间于1624年完成了精度达到小数点后14位的常用对数表.

这项发明很快传遍欧洲甚至也传到了我们中国.人们用对数表和后来发明的机械装置（对数计算尺）来完成那些复杂的计算，极大地提高了计算效率.天文学家约翰尼斯·开普勒将之应用到复杂而精细的天体运动轨迹计算中，通过观测、实验、收集数据、计算和归纳，得到行星运动三大定律，成为对数发明的受益者，著名数学家拉普拉斯感慨地说：“对数的发明减少了劳动量，它使天文学家的寿命延长了一倍.”当时，各种各样的计算尺也成了每个科学家和工程师的心爱之物和忠诚伙伴，人们津津乐道，甚至常常将它们作为礼物，送给刚刚大学毕业参加工作或要结婚的儿女们.

如今，计算机的出现使得再复杂的计算也能在几秒钟甚至瞬间完成，现今几乎所有的计算都是由机器来完成的，正如莱布尼茨所预测的那样.随着对数表在我们中学教材附录中的消失，我们也没机会再看到在工作现场的工程师随手从外衣口袋中掏出计算尺来用的情景了，这默然地告诉我们，那段属于它们的辉煌时代已一去不复返，但是，就算对数失去了在计算中的核心地位，但对数函数却成了几乎所有数学分支的核心.无论是纯数学还是应用数学，它出现在物理学、化学、生物学、心理学、艺术和音乐的各种实际领域的应用中，远远超出了数学的范畴.而我们神圣的e，却俨然成为高等数学的基石！

牛顿把一张张纸，

叠起来，

变成厚厚的笔记本，说，

这叫积分；

又把厚厚的笔记本一张一张撕下，

告诉我们，

这叫微分.

可是，奇妙的ex，

你怎么积它，微它，它还是它，

就像那神通广大的孙猴子，你怎么切，

切下来的还是完整的——

齐天大圣.