数学课揭秘：回顾e的起源与演变

2023-11-19 理论教育版权反馈

【摘要】：简单地说，e就是增长的极限.现行北师大版高中教材中对e的引入放在对数函数中，一个原因是就我们学习数学的进程而言，对数函数在极限、微积分之前；另一个原因是关于e的起源众说纷纭，发现这个后来用e来表示的数的具体时间，至今仍然是个谜，它也可能与对数有关.17世纪初，对数的发明者纳皮尔的著作《奇妙的对数表的描述》中就出现了e.下面让我们一起来回顾一下对数的起源，这有助于我们理解数学家为什么一定要选择以2.71828…

很早以前，金钱问题就成为人们关注的中心话题.生活中再没有比追求富贵和保障财产安全更现实的问题了.对金钱考虑得最多的方面就是利息和贷款偿还.

先让我们来简单地了解一下什么是复利.

假如我们向银行存入100元（本金）钱，年利率为5%，每年计算一次复利，那么在第一年年末，账户上就会有：本金+利息=100+100×5%=100×（1+5%）=105元，如果你不取出来，银行就会自动将这个金额作为本金，重新开始计算新的一年的利息，那么在第二年年末时，账户上的余额将会变成105+105×5%=105（1+5%）=100（1+5%）×（1+5%）=100（1+5%）2.以此类推，第3年年末，账户上的余额将为100×（1+5%）3……我们看到，账户上的余额将以（1+5%）为公比呈几何级数增长.相比之下，单利形式的账户每年只能获得相等的利息回报，如果以100元的本金投资单利，年利率也是5%，那么账户上的金额会每年多5元钱，以等差数列100，105，110，115……增长.显然，不管利率是多少，复利的收益都要比单利来得快，时间越长，快得就越厉害，甚至可以超乎想象.国王奖励国际象棋发明者的故事大家都知道，指数增长的威力大得惊人，爱因斯坦就曾说过，复利是宇宙间最强大的力量.所以如果要积累第一桶金，就不能忽略时间的力量，金钱躲在机会里，机会则躲在时间的洪流里.

从这个例子我们可以得出一个普遍规律，假设我们将本金a元存入账户，获取的复利年利率是r，那么第n年年末，账户余额是

这个公式实际上是一切财务计算的基础，常常被用在银行存款、贷款抵押、分期付款和养老金等多种金融业务的计算上.

如今，商业竞争日趋激烈，时效性也显得越来越重要.银行为方便客户，同时也为更多地回报客户，提高竞争力，银行结息也并不都是一年只计一次利息，而是根据需要计算多次，有一年期、半年期、三月期甚至一周期.如果银行的复利存款年利率是5%，约定每半年结算一次，银行就会将年利率的一半称为期利率，一年内100元本金如果将5%年利率以复利计算两次，半年期利率则为2.5%，那么年末总金额就会增长到 pagenumber_ebook=62,pagenumber_book=54 ，这会比年利率为5%的一年一次复利存款多出6分钱.

假设一年内银行计算复利的次数是n，那么银行会把年利率r除以n作为每次结算的利率，也就是，那么本金a元在一年年末时资金将增长至

100元本金存一年期复利率为5%时不同的结算周期对存款收益的影响

从表中可看出，当n增大时， pagenumber_ebook=62,pagenumber_book=54 也会缓慢增大.你别小看这个增长，如果本金为100亿，增长的金额也会是一笔很大的数目，理论上若客户要求以小时结算，指数将大得惊人，而我们知道，指数的威力实在太大了，客户账户上的余额会增大到什么程度？银行会不会破产呢？

为了更深入地探索这个问题，我们考虑（2）的一个简单情形，即r=1（也就是说，年利率100%，当然还没有哪个银行会慷慨到如此地步，但就数学而言，r作为一个常数，当n很大时，式子中r取一个小数还是取1，对结果影响不大），我们来看看n的增加对式子 pagenumber_ebook=63,pagenumber_book=55 的影响（取a=1，r=1），我们有：

从表中可以看出，随着n的增加，式子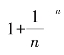 pagenumber_ebook=63,pagenumber_book=55 也随之增大，但越到后面，增长的速度越来越缓.

要计算 pagenumber_ebook=63,pagenumber_book=55 当n越来越大以至于趋于无穷大时的值，需要运用极限运算，这对我们高中生来说，有些困难，数学家通过极限理论已证明，当n→+∞时，式子的值虽然会缓慢增大，但它存在一个极限值，欧拉在他伟大的《无穷小分析引论》著作中用字母e来表示这个极限，定义 pagenumber_ebook=63,pagenumber_book=55 ，这个极限的值约为2.71828，即e≈2.71828.根据欧拉的定义，结合二项式定理和简单的极限知识，我们可以快速地计算e的值.

对于（a+b）n（n∈N），二项式定理展开为

有了以上的准备，我们在二项式定理中，令，则有

显然，当n→+∞时，……的极限值都是0.因此我们有

计算这一无穷级数中的项并将它们相加变得相对简单一些，更重要的是，与前面直接计算相比，它们能更加快速地接近极限值.(www.chuimin.cn)

这一无穷级数开始前8项的和分别是

因为每个和式中的项都在急剧地减小，所以序列迅速收敛.此外，因为每项都是正数，所以收敛过程是单调的：每新加一项都会使结果更接近于极限值.我们可以根据需要，把序列中更多的项相加以达到我们想要的精确度.

每新加一项，都会使结果更逼近准确值，我们想象得到，但似乎永远无法摸到.

似乎我们又看到了有点熟悉的东西，仿佛又看到了圆周率的影子.

随着科学技术的发展，研究的领域也越来越宽泛，人们在研究一些其他的实际问题时，如物体的冷却、细胞的繁殖、放射性元素的衰变，都要研究 pagenumber_ebook=65,pagenumber_book=57 当x趋近无穷时的极限.有趣的是，当x→+∞时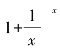，的极限等于e≈2.71828…，当x→-∞时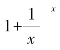，的极限结果也是e≈2.71828…；正是这种无限变化中获得的有限以及从两个相反方向发展而得来的共同的形式，充分体现了宇宙的形成、发展及衰亡的最本质的东西，这就是e被冠以最美的数、最自然的数等美誉的原因吧.

什么是e？简单地说，e就是增长的极限.

现行北师大版高中教材中对e的引入放在对数函数中，一个原因是就我们学习数学的进程而言，对数函数在极限、微积分之前；另一个原因是关于e的起源众说纷纭，发现这个后来用e来表示的数的具体时间，至今仍然是个谜，它也可能与对数有关.17世纪初，对数的发明者纳皮尔的著作《奇妙的对数表的描述》中就出现了e.下面让我们一起来回顾一下对数的起源，这有助于我们理解数学家为什么一定要选择以2.71828…这样一个烦琐的数为底.

强大的对数，

能把乘除变成加减，

把乘方和开方变成乘除.

借用对数表，

科学家和工程师可以快速地完成大型数据的计算，

钱学森离开美国没有带走大量的书籍和笔记，却带了一本对数表，

美国联邦调查局以为是国家机密的密码，将它没收了.

数学课揭秘：回顾e的起源与演变

相关推荐