揭开虚数的奥秘：被遗忘的数学课

前几年浙江卫视《一周立波秀》节目作为中国的脱口秀名噪一时，很受欢迎，其中有一期节目谈到学校教育.我们小学数学的很多应用题中的主人公都叫小明，什么抽水问题、相遇问题、盐酸和水倒来倒去的问题，很是头疼，把小明都要弄成神经衰弱了，不知可怜的小明现在怎么样了，等到我们读初中，知道那些问题都可用方程来解，似乎一下子可控制住了，初中老师经常会说“世界上的任何问题都是数学问题，任何数学问题都是方程问题”，以此来强调方程的重要性，虚数的产生我们就从方程谈起.

一般人都认为，为了使方程x2+1=0有解，虚数就出现了，或者说对一般的一元二次方程，当Δ＜0时，虚数就出现了，这是我们想当然的，历史上真实的情况并不是这样的.

方程作为代数学的核心内容，很多数学家为寻求一元代数方程的一般解法费尽了心血.对于一元一次方程ax+b=0（a≠0），其根为，这个很容易得到，一元二次方程ax2+bx+c=0（a≠0）的情况就复杂一些，其求根公式直到公元7世纪才由印度伟大的数学家婆罗摩笈多首先发现，现行初中教材中通常由配方法给出：

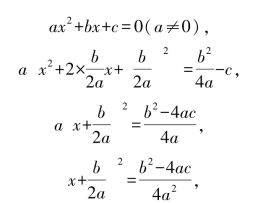
当b2-4ac≥0时，

所以

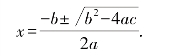
攻克了一元二次方程，数学家一定会向一元三次方程迈进.如何求出ax3+bx2+cx+d=0（a≠0）的一般解？情况比一元二次方程就复杂多了，很长的一段时间内，数学家对解三次方程的态度都是悲观的，他们不知道应怎样解一般的一元三次方程，并认为当时的数学中，求解三次方程，犹如化圆为方一样，是根本不可能的.直到16世纪，这一问题才最终由意大利数学家解决.

围绕解三次方程所发生的故事，激烈、复杂而又扑朔迷离，故事牵涉到博罗尼亚大学的费罗（1465—1526）、布雷西亚的著名学者丰塔纳（1499—1557）和数学史中最奇特的人物——米兰怪杰卡丹（1501—1576）.1545年，卡丹出版了他的数学名作《重要的艺术》，在题为《论三次方加一次方等于常数》的第十一章中，首次展现了三次方程的一般解法，代表了代数学中一个惊人的突破.

卡丹首先巧妙地利用代换，将一般的三次方程ax3+bx2+cx+d=0a≠0化为缺项的三次方程x3+mx=n.

代换是代数中的一个基本技巧.如一元二次方程ax2+bx+c=0a≠0还可以这样解：引入一个新的变量y，令代入，就得到

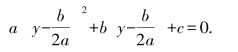
这个代换的关键是使方程的一次项消失了，我们消去by项得到一个缺一次项的二次方程

这样就再现了二次方程的求根公式.

同样，对于ax3+bx2+cx+d=0（a≠0），关键的代换是令，

把代入原方程，得

对这一堆字母，我们前面的代换决定了可以消去y2项，这样，新的三次方程就没有了二次项，如果我们用三次项系数a去除各项，就得到了y3+my=n这种形式的方程，只要解出y，也就不难确定原方程的解的值了.

现在让我们来看看卡丹怎样解决x3+px+q=0（与卡丹方程x3+mx=n等价）的求解.

首先，卡丹用两个数的和表示x，令x=u+v（当然，表示x的方式有很多种.也许卡丹从一元二次方程x2+px+q=0的解的形式中得到启示），三次方程x3+px+q=0改写为

（u+v）3+pu+v+q=0，

利用（u+v）3=u3+v3+3uv（u+v）代数变形将上述方程重新整理为

如果我们选取一种特殊的情形：令（u+v）3=-q，且3uv=-p，那么无疑（*）是成立的.这样我们联立二元方程组

联立（1）（2）消去v，经整理后就得到方程.

初看好像越来越复杂了，因为我们把原来x的三次方程变成了u的六次方程，但是这里关键的是那个六次方程可以看作关于变量u3的二次方程：

而数学家早已从婆罗摩笈多那里掌握了二次方程的解，利用一元二次方程的求根公式，我们可求得，我们选取正的平方根（选负的平方根也可以，最后的结果是一样的）

最后，我们就得到用代数式表示的一般三次方程x3+px+q=0的一个解：

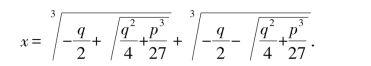
卡丹论证中最精彩的地方在于他用关于u3的二次方程替代了原三次方程，从而发现了将方程降低“一次”的方法，这样，他就从生疏的三次方程进入熟悉的二次方程，这一非常巧妙的方法也开辟了解四次、五次和更高次方程的道路.

例如：卡丹用公式解方程x3+6x=20，即，代入卡丹公式可得：

显然，这是一个“根式解”.令人感到意外的是，这一貌似复杂的式子只不过是数字“2”的伪装而已！我们很容易看出x=2的确是x3+6x=20的解，作为现代的我们，用因式分解容易解方程

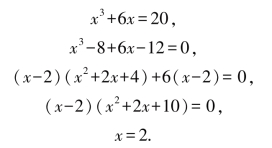
而x2+2x+10=0，Δ＜0，没有实数解.

所以x=2是方程x3+6x=20唯一的实数根，而卡丹公式解出的根是，因而我们有.

卡丹的求根公式是一个很大的成就，但更大的意义在于他还带来了一个重大的谜.

现在，让我们取有历史意义的方程x3-15x=4，即x3-15x-4=0，用p=-15和q=-4代入卡丹公式，我们可得到：

如果说16世纪的数学家对负数尚持怀疑态度，则负数的平方根显然就是绝对荒谬的，所以，卡丹只能认为方程x3-15x=4无解.

然而，对于相对简单的方程x3-15x=4来说，卡丹分明看出了它有一个解是4，现代的我们当然很容易验证出它有三个不同的完美的实数解：

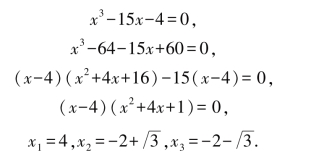
卡丹困惑了！

卡丹在1545年第一次用一个记号来表示一个“无意义”的东西，他在论“不可能把10分成其积等于40的两部分”的一篇讲稿中，指出了这个问题会引出两个不可能的式子和，正如人们早期对待负数的情形，这里也只是把这个“不可能的东西”写下来，给予它一种符号表示而已.

大约又经过了一代人的时间，拉斐罗·邦贝利（约1526—1573）出现了，他在1572年的论文《代数》中迈出了勇敢的一步，邦贝利暂不理会对于的任何潜在的偏见，他求出的三次方：

因为，当然就可以说

同样的道理，还可以得到

那么，再来看三次方程x3-15x=4，邦贝利用卡丹公式求出其解：

就像前面是2的伪装一样，只不过是4的伪装而已，而的出现似乎只是来打酱油的，轻轻地来，又轻轻地走.

邦贝利将“虚数”看作运载数学家从实数三次方程到达其实数解的必要工具，也就是说，我们从熟悉的实数领域出发并最终回到实数，但中途却不得不进入一个我们所不熟悉的虚数世界以完成我们的旅程.

对于当时的数学家来说，这绝对是不可思议的.

正数的平方是正数，负数的平方是正数，零的平方是零，这些观念是如此根深蒂固，因而“负数的平方根”这个“诡辩量”，这个“符号游戏”闯入人们的视线，试图在数学里占有一席之地，其过程注定是曲折的.微积分的两位泰斗虽然在微积分的发明权之争中针锋相对，但在对“虚数”的认识上却出奇地一致，莱布尼茨说虚数是“介于存在与不存在之间的两栖怪物”，由于找不到虚数的物质基础和物理意义，牛顿也认为虚数是荒谬的，正如无理数的发现引起了第一次数学危机这样的波澜，欧洲人迟迟不肯承认负数一样，从虚数的发现，到新的数系的建立和理论上的完善，还有很长的路要走.(www.chuimin.cn)

邦贝利承认这些量是“诡辩的”，但他认为这些“诡辩量”并不是全无用处的，因为它们可以用来作为解决实数问题的工具，邦贝利是第一个认真看待虚数并认识到虚数应用价值的人，经过后续的研究，他还建立了虚数的运算法则.

如果我们抛弃对虚数的偏见，在运算上，它其实完全服从算术上的运算规律，满足交换律、分配律和结合律.邦贝利应当得到赞誉，他也因此成为16世纪最后一位伟大的意大利数学家.

给出“虚数”这一名称的是法国数学家笛卡尔（1596—1650），他在《几何学》中使用“虚的数”与“实的数”相对应，虚数从此流传开来.

1777年，欧拉在《微分公式》一文中第一次用i来表示-1的平方根，首创了把符号i作为虚数的单位，之后随着高斯等人的大量使用，i作为虚数单位在世界上通行起来.

欧拉虽然说过，所有此类式子，如等，它们既不是无，也不比无大，又不比无小，它们纯属虚幻.但他像使用实数一样有效地使用它，提供了虚数的许多应用的实例.受欧拉的影响，其他的数学家在很多数学的推理中间步骤时也用了虚数，而得到结果往往又都被证明是正确的.

1831年，高斯对数的发展做了一个回顾，表达了他对虚数的认识：

“我们的广义算术，其范围远远超过了古代几何，完全是近代的产物.它从绝对整数的观念开始，逐渐扩大其领域.整数之外加以分数，有理数之外加以无理数，正数之外加以负数，实数之外加以虚数.然而这种进步每每在最初时是令人担心的、彷徨的.早年的代数学家叫方程的负根为假根，当所求的量的性质没有相反的量时，这个讲法的确是真实的，然而，正如分数对许多可数的东西毫无意义可言，而我们却在广义的算术里毫不踌躇地承认了它一样，我们不应该只因为有无数的东西不许有其相反的量，就否认了负数有同于正数的权利，因为在其他负数的场合中，负数也具有合宜的解释，所以它的真实性就得到了充分的佐证.这些事情都早已得到承认了，然而虚量，它更像是一种空洞无物的符号游戏，即使那些承认它的伟大贡献的人，明白由于这种符号游戏而对实数关系的宝库做出如此伟大贡献的人，也还是毫不犹豫地否认其有可想象的物质基础.

笔者多少年来就从另一个观点来看待这个数学中的极重要的部分，笔者以为虚数也和负数一样，可以赋予同样的客观存在性……”

高斯的这段话是多么的深刻和富有见地，对我们理解数的发展帮助很大，由此也使我想到，在我们的学习之中，阅读经典原著是多么的重要.

高斯关于“代数基本定理”的证明，必须依赖对虚数的运用，也使虚数的地位得到了进一步的巩固.

高斯（德国，1777—1855）

让我们回到前面一元三次方程的求解上来，现在我们清楚了，与人们普遍认为的相反，虚数不是作为解二次方程的工具，而是作为解三次方程的工具进入数学王国的.显然，在作为x2+121=0的解时，数学家可以轻易地将其排除而得出方程无解的结论.但是，在解x3-15x=4三次方程时，对于在导出x=4时所起的关键作用，就不能如此漠然置之了.因此，是三次方程，而不是二次方程，给了虚数以原动力和它们今天的合法地位.

回到一般的二次方程x2+px+q=0，如果p2-4q是负数，那么方程没有实数根；如果p2-4q正好等于零，那么方程有两个相等的实数根；如果p2-4q是正数，那么方程就有两个不相等的实数根.

上述这些情况可以用抛物线说明.我们画出函数y=x2+px+q的图象，那么这个二次方程的根就是y=0的x的值，即这条曲线与水平轴相交的地方.上面三种情况分别如图2-3（1）所示.

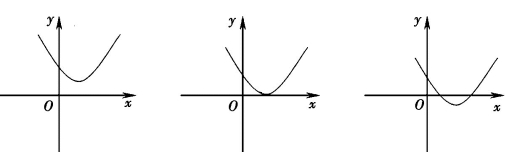
图2-3（1）

对于三次方程x3+px+q=0，我们也可绘制函数y=x3+px+q的图象，同样存在三种基本情况（图2-3（2））：

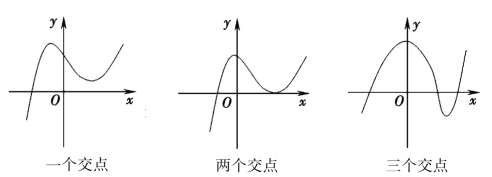
图2-3（2）

有些同学表示怀疑，让我来解释一下.

有趣的是，所有的三次曲线y=x3+px+q都是从第三象限开始，到第一象限结束的.这是因为当x非常“大”的时候（正的或者负的），代数式x3+px+q中的x3项会“淹没”其他项，也就是说，对于“足够大”的x值，x3+px+q的值的符号取决于x3值的符号（“足够大”的尺度取决于p和q的大小）.根据符号法则，负数的立方是负的，正数的立方是正的，所以三次曲线y=x3+px+q的走向一定是从第三象限走向第一象限，这样一来，这条曲线必然与水平轴相交于某个位置，所以三次方程x3+px+q=0一定至少有一个实数根.到底是一个、两个还是三个？它们与的符号有关，我们把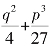称为三次方程的判别式，实际的情况可概括如下：

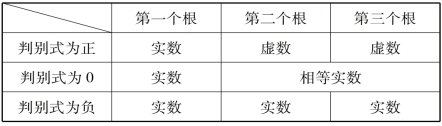
（表中最下面一行再现了卡丹的困惑）

高斯经过系统的研究发现，如果不承认虚数，在实数系内，代数方程有的无解，有的有一解，有的有两解……五花八门，毫无规律，若承认了虚数，那么所有代数方程都有解，而且n次方程不多不少恰好有n个解.而这就是高斯伟大的“代数基本定理”.

有了虚数，凡代数方程，甚至范围更大的超越方程，在新的数域内都有解！

真正使人们相信虚数不是它的应用，更不是逻辑.韦塞尔、阿尔冈和高斯等人对复数的几何表示彻底打消了人们的疑虑.随着解析几何的创立，运动和变量进入数学领域，数学家和物理学家们发现，若把一个平面上的所有各点同数字系统彼此联系起来是非常有用的.我们知道，光有正数和0，数只与一条射线上的点构成一一对应的关系，有了负数，数就能与一条直线上的点构成一一对应的关系，而怎样使数与二维平面上的点构成一一对应的关系呢？虚数恰恰能解决这个问题.

1806年，瑞士人阿尔甘创造性地讨论了的几何表示，这项工作最早可追溯到沃利斯的建议，因为，即，这说明是+1和-1的比例中项，那么它的几何表示就是两个相反单位线段的比例中项的线段，如图2-3（3）所示.这样一来，虚数ai（a≠0）就可对应平面坐标系上的纵轴（原点在横轴上），这样虚数ai（a≠0）就与实数a同样真实（挪威的一个名叫韦塞尔的测量员，也给出了虚数的几何解释，但没有引起人们的注意），1831年高斯详尽系统地表述了平面坐标系几何与复数域数学的等价性.

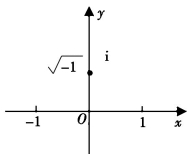
图2-3（3）

依照上面的表述，一个实数代表平面坐标系中x轴上的一点，设a是这样的一个实数，A是它在x轴上的代表点，若用i乘之，ai等同于将向量按逆时针方向转一直角，所以a·i这个数就用y轴上的A′代表了，若再乘以i我们即得a·i2=-a，而其代表点A″又在x轴上了……以此类推，依次连转四个直角，该点就回到它的原来的位置，如图2-3（4）所示.

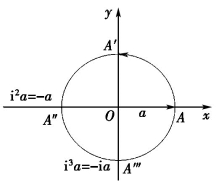
图2-3（4）

这样，对任一实数a（a≠0），都有唯一的虚数ai与它对应（这样的虚数叫纯虚数），它就如同实数在镜子里的影像一样，形影不离，全部实数落在x轴上，与之对应的全部纯虚数落在y轴（除点（0，0））上.

纯虚数bi（b≠0）还与实数a结合起来构成形如a+bi类的数.

高斯用两个向量的合成向量来表示数a+bi，A是实数a的代表点，B是纯虚数bi的代表点，a+bi代表了以OA，OB为边的矩形对角线的末端C点，所以复数a+bi相当于平面坐标系中横坐标为a，纵坐标为b的点C，如图2-3（5）所示.这样一来，若点P和点Q所代表的两个复数相加，则等同于将向量和用平行四边形法则相结合；用一个实数与点P代表的复数相乘，如这个实数是3，那便是将向量伸长3倍，乘以i就是按逆时针方向旋转一直角，等等.

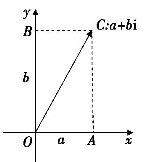
图2-3（5）

在此基础上，高斯还将表示平面上同一点的两种不同的方法——直角坐标和极坐标加以综合，统一于表示同一复数的代数式和三角式两种形式中（如图2-3（6）），进一步阐述了复数的乘法和除法的几何意义，至此，复数的几何表示就完整和系统地建立起来了.这种具体的解释，使得邦贝利的幽灵变得有血有肉，它从复数里除去了“虚”象而代以一种“形”象.

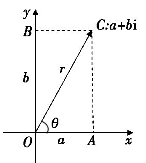
图2-3（6）

1832年，高斯第一次提出了“复数”这个名词，他把形如a+bi（a，b∈R）的数统称为复数（当b=0时，为实数；当b≠0时，为虚数），利用直角坐标系来表示复数的平面，叫作复平面.x轴叫作实轴，y轴除去原点的部分叫作虚轴，原点表示实数0，原点在实轴上.复平面内的每一个点，有唯一的复数和它对应，反过来，每一个复数，在复平面内有唯一的点和它对应.复数集C和复平面内所有的点所成的集合构成一一对应关系.

复平面的建立，揭开了虚数神秘的面纱.为了纪念高斯的伟大功绩，人们通常也称上述描述的复平面为高斯平面.高斯平面的出现在数学史上是一个转折点.

就这样，被人们看作一种空洞的符号游戏的复数，由于某种因缘际会导出了真实的结果，因为它们有用，所以保证了其存在的正当理由.它和任何实数的存在一样，一方面，它们完全服从算术的运算律，它们也是忠实的数；另一方面，它们又是平面上的点的完整的化身，成为一种合乎理想的工具，适用于把平面上的图形之间的复杂的几何关系变成数的语言，成为解决繁难问题的有力手段.复数在力学、电学、地图学、航空学等领域的应用十分广泛，显示出其非凡的魅力.

让我们简单来回顾一下，从人类开始计数，到复数体系的建立，其发展的过程是这样的：

当代数学家是怎样看待数系的呢？它就是N，Z，Q，R和C这些字母，分别代表自然数集，整数集，有理数集，实数集和复数集.

数学家把数看作一组层层相嵌的俄罗斯套娃：

最内层的套娃：自然数，1，2，3……

外一层的套娃：整数，自然数加上0和负整数.

再外一层的套娃：有理数，整数加上正的分数和负的分数.

更外一层的套娃：实数，有理数加上无理数.

最外一层的套娃：复数，实数加上虚数.

复数体系的建立，人类经历了漫长的探索和斗争过程，数的每一次扩充在最初都伴随着担心与彷徨.今天，我们应用的数系，已经构造得如此完备和缜密，以至于在科学技术和社会生活的一切领域中，它都成为基本的语言和不可或缺的工具.在我们得心应手地享用这份人类文明的共同财富时，是否想到在数系形成和发展的历史过程中，人类的智慧所经历的曲折和艰辛呢？

人类的探索精神永无止境，新的问题：是否还能在保持数的基本性质的条件下对复数进行新的扩张呢？答案是否定的.我们知道，实数代表的是一维直线，复数代表的是二维平面，当爱尔兰数学家哈密尔顿（1805—1865）试图寻找三维空间的类似物时，他发现必须满足两个条件：一是他的新数要包含4个分量（他称这新的数为“四元数”），二是他必须牺牲乘法的交换律.这预示着复数是传统观念下数系扩张的终点.

数系的扩张虽然就此终结，但“四元数”的出现却打开了通向“抽象代数”的大门.有待于同学们今后进一步学习和研究.

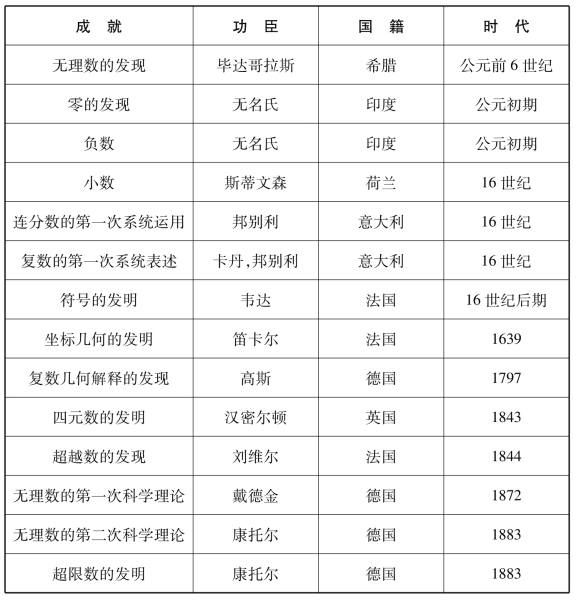
附录：数的发展进程中的里程碑