公元前500年，被遗忘的数学课揭示了无理数发现的惊人事实

2023-11-19 理论教育版权反馈

【摘要】：公元前500年，毕达哥拉斯学派的弟子希伯索斯根据毕达哥拉斯定理发现了一个惊人的事实：一个边长为单位长的正方形的对角线的长度不能用数来表示，如图2-2，线段AB不能用数（有理数）来表示.图2-2因为，若可用一个最简分数来表示，不妨设：，两边平方得m2=2n2……

公元前500年，毕达哥拉斯学派的弟子希伯索斯（Hippasus）根据毕达哥拉斯定理发现了一个惊人的事实：一个边长为单位长的正方形的对角线的长度不能用数（整数或整数比）来表示，如图2-2（1），线段AB不能用数（有理数）来表示.

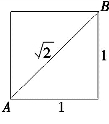
pagenumber_ebook=44,pagenumber_book=36

图2-2（1）

因为，若可用一个最简分数来表示，不妨设：

（m，n是整数，且不可约），两边平方得m2=2n2……（1），这样m2必为偶数，从而m为偶数，设m=2k（k为整数），代回（1）式，得4k2=2n2，即n2=2k2，这样n2又必为偶数，所以n也为偶数，m，n皆为偶数与假设m，n不可约矛盾.

所以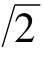， pagenumber_ebook=44,pagenumber_book=36 不能有分数的形式，也就是说线段AB的长度是不能用“数”来表示的.

毕达哥拉斯学派通过建立数轴，他们凭经验与直觉，认为数轴上的点与有理数之间建立了一一对应的关系，达到了算术与几何的和谐统一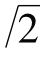，“ pagenumber_ebook=44,pagenumber_book=36 ”的出现使他们意识到，没有任何有理数能与数轴上这样的一点P对应（如图2-2（2）所示，OP为正方形的对角线），进一步的研究发现，像P这样的点还有很多很多，数轴上到处有“缝隙”.

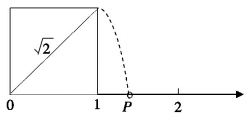
pagenumber_ebook=44,pagenumber_book=36

图2-2（2）

毕达哥拉斯的“万物皆数”面临崩溃的局面，使该学派陷入一片惶恐，于是他们极力封锁这个发现的流传，他们把这种“不可公度”的数叫Alogon（“阿洛贡”，即“不可说”之意），希伯索斯被迫流亡他乡，不幸的是，在一条海航线上他还是遇到了毕氏门徒，希伯索斯被装进麻袋并被残忍地扔进了大海.

“不可说”的量的出现，动摇了当时占统治地位的毕达哥拉斯的“万物皆数”的世界观，导致了第一次数学危机，是数学史上的一次重要事件.

确定正方形的对角线，揭示出数学上一种新实体的存在：这种实体在有理数域中是没有立足之地的，人们感到有理算术的不够用了.

代数方法的进一步发展也同样体现出有理算术的局限，因为有理数系连最简单的二次方程都不能完全胜任.数域的扩充不可避免.

后来的人们把毕达哥拉斯的“有比数”叫有理数，把毕达哥拉斯的“不可说”叫无理数.公元前370年，柏拉图的学生欧多克萨斯（Eudoxus）用公理化方法创立了新的比例理论，在几何上给出了无理数的解释，总算把无理数引入数学大家庭，从而使数的疆域向前迈进了一大步.

第一次数学危机对希腊数学产生了深远的影响，既然几何量“正方形的对角线（ pagenumber_ebook=45,pagenumber_book=37 ）”不能完全由整数或其比来表示，但另一方面所有的数都可以用几何量表示出来，因此，希腊人认为几何比算术占有更重要的地位，这使在其后的数学发展中，几何对算术的优势支配了希腊数学近千年.同时在理论上，希腊人也明白了，直觉和经验都不是绝对可靠的，推理证明才是可靠的，因而，希腊人更加重视逻辑和演绎推理，并在亚里士多德手中完成了古典逻辑学的创立.从此，希腊人开始从“自明”的公理出发，经过演绎推理，形成了以欧几里得的《几何原本》为代表的公理体系，这是数学思想史上的一次革命，为数学的发展做出了杰出贡献.

虽然无理数由“不可说”变成了“可说”，无理数使数轴上的“空隙”都被填满，同时也使很多代数方程能够求解，但对它究竟是不是实实在在的数，却仍然困扰着一些人，直到16世纪，随着小数的发明和应用，人们才逐渐给无理数下了一个我们耳熟能详的、比较明确的定义——无限不循环小数，而无理数的理论直到19世纪才由德国数学家戴德金和康托尔等人最终建立起来.

值得一提的是，远在公元3世纪的魏晋年代，中国古代数学家在处理开方时，也不可避免地碰到根为无理数，对于这种“开之不尽”的数，刘徽在《九章算术》注释中用“求其微数”来处理，实质上就是用十进小数来无限逼近无理数，这本是一条完善无理数理论的正确道路，但是，中国传统数学关注的是具体数量的计算和应用实际，对数的理论的研究并没有太大的兴趣，与在理论上揭示无理数的本质失之交臂.

从数系的发展过程来看，自然数、分数、无理数在公元前就出现了，但奇怪的是，负数的出现就晚多了，而且人们从使用负数到接受负数的概念也经历了漫长的时期.

我们初中数学教学中负数的引入通常从三个方面来讲：一个是在减法运算中，当被减数比减数小时，负数就出现了，用专业一点的话来说，有理数系对加法、乘法和除法运算是封闭的，为了使得减法运算在数系内也通行无阻，负数的出现就是必然的了.另一个是人们在日常生活中经常会遇到各种相反意义的量，比如零上温度和零下温度，海平面之上和之下，收入与支出，借贷与负债，等等，在这些事物中，负数的出现也显得非常自然.还有一个是从代数上看，负数的产生在很大程度上也是由于解方程的需要，因为在解方程的过程中常常会碰到较小的数减较大的数的情况（虽然不一定就得到负根），为了使方程能够解下去，数学家暂时也承认了负数.我国的《九章算术》中在对方程两行之间加减消元时，必须引入负数并建立正、负数的运算法则，刘徽的注释也对负数的运算法则做了阐述.公元3世纪，希腊数学家丢番图的著作中也用到了负数，但他只给出方程的正根（负根被其称为“假根”而舍去）.在印度，数学家婆罗摩笈多于公元628年认识到负数可以是二次方程的根（一元二次方程求根公式就是被婆罗摩笈多发现的）.但在欧洲，直到16、17世纪，大多数数学家在研究负数存在的合理性方面还不承认负数是数，韦达知道负数的存在，但他完全不要负数，帕斯卡认为0表示什么也没有，从0中减去4是纯粹的胡说，帕斯卡的朋友阿润德也跟着起哄，提出了一个有趣的说法来反对负数，他说（-1）∶1=1∶（-1），较小的数与较大的数的比怎么能等于较大的数与较小的数的比呢？直到1637年，法国人笛卡儿发明解析几何，创建了坐标系，负数得到实际的解释，欧洲人对负数的意义才有了真正的领悟.(www.chuimin.cn)

至此，实数体系的发展大致可以告一段落.现在我们知道了，正是因为有了负数，原来的数才被命名为正数；正是因为有了无理数，原来的数才被命名为有理数.数的扩充从时间上来讲，它的顺序是自然数、分数、无理数、0、负数.最后完备的实数体系的结构是

pagenumber_ebook=46,pagenumber_book=38

最后，让我们来简单了解一下实数理论，1871年，德国数学家康托尔第一次给出了实数的严格定义.实数的一些初等性质如下：

1.运算的封闭性：实数集R对加、减、乘、除（除数不为零）四则运算具有封闭性，即任意两个实数通过加、减、乘、除运算，结果仍为实数.任何实数都可以开奇次方，结果仍是实数，只有非负实数才能开偶次方，其结果也是实数.

2.有序性：实数集是有序的，即任意两个实数a，b，必定满足下列三个关系之一：a＜b，a=b，a＞b.

3.传递性：实数的大小具有传递性，即若a＞b，b＞c，则有a＞c.

4.稠密性：实数集R具有稠密性，即任意两个不相等的实数之间存在无限多个有理数与无理数.

5.唯一性：任一实数都对应直线（数轴）上的唯一点，反之，直线（数轴）上的每一个点也都唯一地表示实数.于是，实数集R与数直线（数轴）上的点建立了一一对应的关系.如图2-2（3）.

pagenumber_ebook=47,pagenumber_book=39

图2-2（3）

德国数学家克罗内克曾说，上帝创造的整数、分数、无理数和负数都是被发现出来的，每一次发现新的数都是为了解决“不这样就无法回答”的问题，到文艺复兴时期（14-16世纪），数学家认为他们已发现了天地万物中的一切数，所有的数可以被看作落在一条直线（一条无限长的、以零为中心的直线，即数轴）上，整数沿数轴等距离地分布，正数在零的右边延伸到正无穷，负数在零的左边延伸到负无穷，分数占有整数之间的位置，无理数则散布在分数之间，所有数都已在位置上准备好回答任何数学问题，在数轴上已经没有多余的地方来表示新的数了.至此，我们完成了从自然数到实数的一次全程的旅行.

数系理论的历史发展表明，数的概念的每一次扩张都标志着数学的进步，但是这种进步并不是按照数学教科书的逻辑步骤展开的.公元前，希腊人关于无理数的发现就暴露出有理数系的缺陷，然而实数系的完善却直到2000多年后的19世纪才得以完成，负数早在《九章算术》中就已被我国数学家所认识，然而15世纪的欧洲人仍然不愿意承认负数的意义.它显示了数学发展的进程大多是不合常规的，而这一幕在数学史上最古怪的一个事件中得到更加淋漓尽致的体现.

在人们还远没有建立实数的理论基础、尚未完全理解负数、无理数时，他们的智力又面临着一个新的“怪物”的挑战，这就是我们接下来要重点讲述的内容.

一个神秘而又似乎不可能的数字，

它似流星，瞬间划破夜空，

你还没来得及欣赏它的美丽，

又瞬间逝去.

公元前500年，被遗忘的数学课揭示了无理数发现的惊人事实

相关推荐