自然数的产生：有古罗马数字、古埃及数字，现代数字是什么？

2023-11-19 理论教育版权反馈

【摘要】：；还有古罗马数字：Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅵ，Ⅶ，Ⅷ，Ⅸ，Ⅹ，这种表示法在钟表盘上一直沿用至今，另外古埃及用符号来表示数，说来奇怪，中国的麻将牌中依稀还可见到古埃及数字的影子.随着文明的发展，数字的表示最后实现大统一，现在世界统一用什么来表示数字呢？

数的产生，远在有史以来，详情已无法深究，如果我们用现代印第安人的智力来推断我们远祖的文明，人类在进化的愚昧时期也是非常幼稚的.早期人类的数决不会大于3，古人“三人行，必有我师焉”“三人成虎”中的“三”其实都是多的意思.但是，在经历了一系列特殊的环境，人类在极为有限的数觉之外，学会了另一种特殊的技巧，这种技巧给人类未来的生活带来了巨大的影响.正是由于这种人类独具的特性，我们取得了描述宇宙的惊人成就.

这种特殊的技巧就是计数.

也正是计数，才使具体、不同质表达多寡的概念结合为统一的、抽象的数的概念.罗素曾说：“不知经历了多少年，人类才发现‘一对锦鸡’和‘两天’同是数字‘2’的例子.”前者是原始人的特点，后者则是数学发展的前提.

计数需要解决的第一个问题是用符号来表示一切数.

不同国家和地区的人们用不同的符号来表示数.如我们中国古代用文字表示数：一，二，三，四，五，六，七，八，九，十；古希腊用希腊字母表示数：α表示1，β表示2，γ表示3，δ表示4……；还有古罗马数字：Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅵ，Ⅶ，Ⅷ，Ⅸ，Ⅹ，这种表示法在钟表盘上一直沿用至今，另外古埃及用符号 pagenumber_ebook=39,pagenumber_book=31 来表示数（这可能来自古代“刻痕划印”“结绳计数”的方法），说来奇怪，中国的麻将牌中依稀还可见到古埃及数字的影子.

随着文明的发展，数字的表示最后实现大统一，现在世界统一用什么来表示数字呢？

学生：阿拉伯数字。

老师：对，是1，2，3，4，5，6，7，8，9，但注意这并不是阿拉伯人发明的，而是印度人发明的，因经阿拉伯流传至欧洲，人们误以为是阿拉伯数字.为了缅怀印度数学家的伟大功绩，算用数字1，2，3，4，5，6，7，8，9现在被称为印度-阿拉伯数字.

显然，不可能发明一百个符号来表示一百以内的数，发明一万个符号来表示一万以内的数，如何用较少的数字符号来表示一切数呢？

这就需要确定数的进制.

的确，我们的十个手指毫无疑义地影响了我们数制基底的选择，事实上，正是我们的手指，教会了人类计数.

英国人R.梅森（Mason）讲过第二次世界大战时的一个有趣的故事：

当印度和日本两国爆发战争时，一个日本姑娘正在印度，为了避免可能会遇到的麻烦，她的朋友让她冒充中国人，有人怀疑她的身份，要求这个姑娘用手指依次表示1，2，3，4，5，她踌躇了一下以后，先伸开她的手，然后把手指一个一个地蜷上，一下子就把身份暴露了.因为中国人和英国人一样，在数数时是先把手蜷拢，然后一个一个地打开.

在现代文明中，除了小孩初学计数的时候还用手指和我们自己有时候为了加强语气还用手指外，屈指（弯着指头计数）的技术已经被淘汰了，十进制的表示法看起来那么自然，使我们很容易低估屈指和十进制在数学史上起过的重要作用和功绩.

基底确定后，位置原则又是一个深远而重要的思想，而“0”的发现永远标志着人类最伟大的、独一无二的成就.无论是中国古代数字还是古罗马数字抑或是古希腊数字，它们不及印度-阿拉伯数字的地方，就是它们都没有创立与零等同的数字，没有代表空位的数字（“0”的位置原则，便于区别23与203或230）.通过十进制和位置原则，我们就可以运用少量的符号（0，1，2，3，4，5，6，7，8，9）通过不同的排列（每个数符不但有绝对的值，而且还有位置的值）来表示一切数.

现代人利用印度-阿拉伯数字，采用十进制和位置原则，可以毫无困难地进行数的表达与运算，它是那样自然与简便，但这并不意味着大家都真正懂了计数的方法.

我们不妨来进行一项测试.有谁知道一百二十三，即123的含义是什么？

学生上台演板：123=1×100+2×10+3×1=1×102+2×101+3×100.

老师：很好！那么请你继续用五进制表示一百二十三.

学生：老师，我还真不会.

老师：这个也不怪你，有谁能写出来吗？

（有几位学生举手）

老师：好，你来演示.

学生上台演板：（123）10=100+20+3

=4×52+4×51+3×50

=（443）5.

老师：正确！5进制能表示一切数吗？

学生：能.

老师：需要用几个数字？

学生：需要0，1，2，3，4，共5个数字.

老师：很好.你是否能继续用二进制表示123呢？

学生：27=128，26=64，25=32，24=16，23=8，22=4，21=2.

（123）10=64+32+16+8+2+1

=1×26+1×25+1×24+1×23+0×22+1×21+1×20(www.chuimin.cn)

=（1111011）2.

老师：不要小看这个内容，真正懂了的人不见得很多，大家都习以为常用十进制，好像都懂似的，不是吗？

我们中国古代文明有着辉煌灿烂的成就，就拿数的进制来说，我们有五进制，算盘中有“六上一去五进一”口诀，选举的时候我们用“正”字统计选票；我们有十二进制，如铅笔仍按“打”计算，一打12支，一罗有12打；更奇怪的还有十六进制，“半斤八两”就是这样来的.

在时间和角的度量方面，现在仍使用六十进制，我们所居住的地球表面上的点的位置采用经纬度来描述，也用几度几分几秒的六十进制.

除十进制外，二进制注定有其独特的魅力.以2为基底的好处是符号的经济（只需用0和1两个数字）和演算的简单，每种数制都需要确定一个加法表和一个乘法表，十进制是九九表，我们都背过，而在二进制中，它们就简化得只剩下了1+1=10和1×1=1，不过，这种好处却被书写的麻烦抵消了，如十进制数4096=212，在二进制中则要写成1000000000000，令人头痛.但就为了二进制这种0和1的雅致，大哲学家莱布尼茨曾赞叹说：“用一从无，可生万物.”他想象，1代表上帝，0代表混沌，上帝在混沌中创造出世界万物，正如在二进制的计数法中用1和0能表示一切数一样.

现代计算机采用的就是二进制，而莱布尼茨正是计算机的先驱和鼻祖.随着电子科技的迅猛发展，二进制得到异乎寻常的发展，在电子技术中用0和1来表示脉冲信号的有无，通过电路用二进制来进行数据的存储、运算.今天，基于二进制的数字技术几乎涵盖了我们所有的领域，全方位地影响着我们的生活和人类历史的发展进程.

关于记数法，拉普拉斯曾深情地说：

“用十个记号来表示一切的数，每个记号不但有绝对的值，而且有位置的值，这种巧妙的方法出自印度，这是一个深远而又重要的思想，它今天看来如此简单，以致我们忽视了它的真正伟绩.但恰恰是它的简单性以及对一切计算都提供了极大的方便，才使我们的算术在一切有用的发明中列在首位；而当我们想到它竟然逃过了古代最伟大的两位人物阿基米德和阿波罗尼奥斯的天才思想的关注时，我们更感到这成就的伟大了.”

人类采用十进制其实是一种生理上的凑巧，因为十进制的基底除了“十指分明”的优点外，本身并没有很多可称道之处.实用家坚持要用有最多因数的数如十二之类为基底，后期的有些数学家则主张用质数作基底，因为用质数做基底，分数表示的一个数只有一种形式，不用化简，简单明了，没有了之类的混淆.

然而，几千年来，人们用十进制的传统已经根深蒂固，深入骨髓，融入基因，谁要想去改变它，看来都是很滑稽的，就让人类一直用十进制来计数吧.因为这会使我们意识到，人类精神生活的这一最重要的规则，原来源于我们人类自身，这会使我们感到骄傲.正如古希腊普罗塔拉哥的名言：人类乃万物的尺度.

位置值制是数系发展的第一个里程碑，标志着人类掌握的数的语言，已从少量的文字个体，发展到了一个具有完善运算规则的数系.人类第一个认识的数系，就是我们常说的“自然数系”.

自然数是人类在计数过程中自然产生的抽象概念.

随着人类认识的发展，自然数系的缺陷慢慢就显露出来了，作为量的计量，它只能表示一个单位量的整数倍，而无法表示一个单位量的部分.在日常生活中，很多时候我们不仅要计量单个对象和它的倍数，还要计量多种量，如半个苹果和许多不是某个单位整数倍的量，如长度（距离）、质量和时间等，为了满足这些简单的计量的需要，就要用到分数.

另一方面，就自然数的加、减、乘、除四则运算而言，显然，两个自然数的加法和乘法，得到的结果仍是自然数，这种情形在数学上被称为“自然数对于加法和乘法是封闭的”，显然，作为运算手段，在自然数系中只能施行加法和乘法，而不能自由地施行它们的逆运算，如除法.分数的出现，弥补了这一缺陷，分数伴随着自然数的产生和数的运算在公元前很早就有了.

但请注意，不要以为3-5=-2，就认为负数也会自然而然地出现，因为古人显然会以从3个里面取5个是荒谬的而不予考虑.

这样，在早期的数的体系中，只有自然数（正整数）和分数（两个正整数的商）这两种数，人们把这两种数统称为有理数，早期的数的体系得以确立.有理数是英文rationalnumber的直译，ratio原本是“比”的意思，因此rationalnumber（有理数）称其为“有比数”更合适.

有理数还有一种简单的几何解释：在图2-1（1）所示的数轴上，标一段线段作为单位长，令它的左端点和右端分别表示数0和1，则可用这条数轴上的间隔为单位长的点的集合来表示全部正整数，对于分数而言，以m为分母的分数，可以用每一单位间隔分为m等分的点表示，于是每一个有理数都对应着数轴上唯一的点.当然，反过来，数轴上的任一点都可对应一个有理数.在早期的数学家看来，全部有理数对应的点可填满整个数轴（即使是现在，尚未深入了解数轴性质的人也会这样认为，通常的感觉也是如此）.这样，有理数与数轴上的点便建立了一一对应的关系，希腊人将算术概念转变成了几何概念，有理数系的几何表示也得以建立.

pagenumber_ebook=43,pagenumber_book=35

图2-1（1）

对于实践中出现的各种量的计量，早期人类凭经验与直觉，认为有整数和分数就足够了.

在数学上，条条大路都会回到希腊.

毕达哥拉斯是古希腊的大哲学家、数学家，他证明了许多重要的定理，其中最有名的是以他的名字命名的毕达哥拉斯定理（也就是我们所说的勾股定理）.毕达哥拉斯将数学知识运用得纯熟之后，觉得数学不能只满足于用来计算，于是他把数从数学领域扩大到哲学领域，用数的观点去解释世界，他提出“万物皆数”（这里所谓的“数”指的是自然数，即正整数）的观点，整数的元素就是万物的元素，世界是由整数组成的，世界上的一切没有不可以用整数来表示的（分数因为是整数的比，自然也含在其中），整数本身就是世界的秩序.他的门徒们把这种理论加以研究发展，形成了在当时占统治地位的强大的毕达哥拉斯学派.

然而，正当毕达哥拉斯学派呈现一片欣欣向荣的景象的，他的“万物皆数”的信仰统治学术界的时候，裂痕出现了，根基动摇了，而充当掘墓人的正是毕达哥拉斯本人.

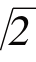pagenumber_ebook=43,pagenumber_book=35