被遗忘的数学课：圆周率的定义与近似值

好熟悉，认识你太久

好陌生，你的故事太长

若我驻足，也算了解了你

若我继续，能否看到你的尽头

同学们，今天我们用两个小时的时间，给大家做一个数学讲座，既然是讲座，请大家放松心情，积极参与讨论，首先，我想用几分钟来泛泛而谈，然后我们一起做数学.

同学们都已学习了十来年的数学，我肯定，数学对不同的人意味着不同的体验，这位同学，谈谈你对数学的认识.

学生：数学是研究现实世界的空间形式与数量关系的科学.

老师：同学们还是喜欢用标准答案回答问题.大家可能不知道，这句话是19世纪恩格斯说的.当然，现代数学的发展，其内容与形式已不再是空间形式和数量关系所能完全涵盖的了.

还有谁说说？

学生：数学是一门有用的学科，对我们来说，学习数学是一项必须完成的任务.

学生：我们很少听数学讲座，平时的课堂内容比较枯燥、无趣，我们学数学完全是为了解题，为了考试.

学生：数学在我们的生活中十分常见，它被运用到各个领域，为我们创造了一个又一个奇迹.

老师：能举个例子吗？

学生：可以。工厂生产、飞船上天都要用到数学，数学还能帮助人们分析理财.

老师：很好！

学生：数学既能开阔人的思维，又能推动文明的进步和发展.因为高考，我们很少有机会来欣赏数学，但我们仍然能在解题时尽力去寻找那一丝一缕的和谐与美妙，而那种解出了数学难题后的喜悦，真是无法言语，只有自己才明白.

老师：认识很有底蕴啊，奖你一本笔记本，还有谁补充吗？

学生：数学是枯燥的公式和复杂的图形，上数学课容易打瞌睡，碰到考试就头痛，我数学学得很不好，非常苦恼.

老师：对数学头疼的人大有人在，你不必苦恼，慢慢来吧.

现在让我们切入正题，从一个简单的地方开始，一起来分享一个数，这个数对我们来说既熟悉又陌生.说熟悉，因为大家从小学就知道它，并且一直用到现在，将来读大学还要与它打交道，它在数学、生活、宇宙自然中无处不在；说陌生，是因为同学们对它的历史和内涵、它的神秘性和魅力又知之甚少.那么这是一个怎样的数呢？哪一个数值得我们高中学生用宝贵的几个小时来“戏说”呢？

学生：π（窃窃私语，也有说e的）.

老师：对，今天我们讲的就是圆周率，一个神奇的数，在所有数学符号中，最古老又最吸引人的符号，也许就是π了.今天我们将从圆周率的历史、计算方法、圆周率的性质和它的未解之谜等几个方面来充分了解它、认识它，领略它那无限繁华的风情.

（学生有的很感兴趣，有的显得平平淡淡，还有的在埋头写什么东西）

老师：先问一个简单的问题，什么是圆周率？

学生：圆周率是π.

老师：那么π是什么？

学生：π就是3.14.

老师：刚才这位同学的回答，反映了我们中学生数学学习的一种常态，当然，也表明我们教学中存在的一些问题.谁说说圆周率的定义？

学生：圆周率显然是一个比率，是圆周长与直径的比值，不对，好像是与半径的比值.

老师：数学是不能用“好像”来说话的，到底是半径还是直径呢？

学生：C=2πR，S=πR2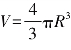，，应该是半径.

老师：是嘛，这个问题很简单吧，我们就是这样学数学的啊.

（笑声）

学生：圆周率是圆周长与直径的一个比值，用π来表示，它的近似值是3.14.

老师：这个回答很到位！体现了我们重点中学学生的水平.（笑）

π的语源是希腊语“周围之意”的字头（希腊文的第16个字母）.圆周率是圆周长与直径之比，即，取直径为1个单位，圆周率即为π，但古希腊人并没有用π代表圆周率.直到1706年，英国数学家琼斯在《数学概论手册》一书中才首次用π代表圆周率，但由于他的名气太小，他的书在数学界也没有什么分量，这种表示法并没有引起人们的响应.30年后，瑞士大数学家欧拉也开始在著作中提到符号π，后来还将符号带进了他那伟大的《无穷小分析引论》，这符号从此风行起来，大家都有样学样，世界也跟着，还是名人效应啊！

大家对π似乎都很熟悉，但有些同学对圆周率的定义竟然不清楚.要正确认识π，我们首先要搞清楚的是数学家为什么要定义圆周率这么一个概念.这个问题不搞清楚，我们对π的认识就如水中月、镜中花，空中楼阁.学习要善于从源头上多问为什么，让我们先从圆开始谈，然后再一起去了解π这个“所以然”.

我们知道，圆是宇宙中最简单、最常见的形状，雨滴落在池塘里，正圆形的涟漪不断扩大；从空中往下看，树冠也是以圆形向外延伸，这样整个树枝接触阳光的面积会最大；就连行星和恒星也不例外，他们在空中以圆球的形式存在着.对人类的早期文明而言，每天高挂在天空的明月和太阳，一直是未知力量和神秘的象征，甚至在文明开始之前，人类就曾利用木桩和绳子，在沙地里画出一个个大小不一的圆，公元前800年，出现过圆形的住家和祭坛，也许是为了祭拜大地之母.

圆也是人们最早认识和研究的一种曲线（椭圆、抛物线、双曲线等都是相对晚些时候才被发现的曲线）.托尔斯泰在其短篇小说《一个人需要很多土地吗？》中讲了一个土地划分的故事，约定一个人从早晨太阳升起开始走，直至太阳下山又回到起点，他所走的路径围成的区域即为他拥有.他该沿怎样的路径行走呢？我们可以假定他一天中走路的时间是定值，他的平均速度也可认为是定值，那么，他在这一天中走的路程也是一个定值，而我们知道，周长一定，圆的面积最大，这样最佳的路径是走一个大圆圈.

冬天里的猫等动物都喜欢蜷作一团，是因为体积一定，球的表面积最小，所以蜷作一团，散发的热量就最少.

小时候我们都玩过吹泡泡游戏，拿一根铁丝，将它弯成一个形状，蘸一下肥皂水后开始吹气泡泡，奇怪的是当初无论我们把铁丝弯成什么形状，最后吹出来的气泡一定是一个个色彩斑斓的球形，这是因为气泡总是试图寻找一种需要最少能量就能塑成的形状，而自然是如此的高效，这正是自然界如此偏爱球形的原因吧.

圆也广泛地存在于人们的文化思想中，“有钱无钱，回家过年”图的是家人新年团聚，团团圆圆；甚至小孩吃饼干，有时也喜欢哭闹着“不吃方的，吃圆的”，圆真是无处不在！

（福建土楼，建于唐朝公元618年左右）

对古人来说，土地的测量是不可少的，圆的直径的测量很容易，但其周长尤其是面积的测量就要费一些周折，因为生产、工程和建筑的需要，轮子（滚筒、滑轮）的普遍使用，人们很容易想到一个问题，把一个轮子在平面上滚一圈，可以滚多远？通过测量容易得到这个滚动的距离.测量多了，人们慢慢就得到一个经验，轮子滚动的距离与轮子的直径的比总是一个略大于3的值，不论轮子是大还是小，结果都是这样，只是这个略大于3的值有时是3.15，有时是3.09，等等.为了简洁和方便，近似地就看作3吧，这样下次要知道圆的周长，只要测量圆的直径，然后乘3就可以了.

圣经《列王纪》描述了所罗门王神殿内祭坛的规格“……他又铸了一个铜海，样式是圆的，高五肘，径十肘，围三十肘”，我国古代战国时期数学经典《九章算术》中也有“周三而径一”的记载，这说明，古代在工程、建筑等实践活动中都使用π=3这样一个方便的值.

显然，圆周率比3大一点点，但到底大多少，没有人能准确地得到一个确定的数值，所以，认识到对任意一个圆，圆周长与直径的比是一个常数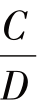（=常数，即C=πD），这样的质的跨越是一个很了不起的成就.

欧几里得综合前人的实践活动，在理论上进一步完善了圆的研究，他在《几何原本》中证明了两个圆的面积比等于两个圆直径的平方比，即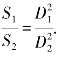.换一种形式为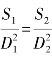，也就是说，对不同的两个圆，圆面积与其直径的平方比是相等的，这就意味着对任意一个圆，圆面积与其直径的平方之比是一个常数，即存在一个常数k，使得，即S=kD2.但是一维常数π（C=πD）与二维常数k（S=kD2）之间相互有什么关系？欧几里得没有发现这种联系.

江山代有才人出，古希腊辉煌的数学文明在阿基米德时代达到了顶峰.阿基米德在论文《圆的测定》中解决了这个问题，阿基米德用一种所谓的“双重归谬法”证明了这样一个命题：如图1-1，圆的面积等于一个直角三角形的面积，这个直角三角形的一条直角边等于圆的半径，另一条直角边等于圆周长，用符号语言表示即.

图1-1

阿基米德乘胜追击，他又证明了两个球的体积之比等于两个球直径的立方之比，即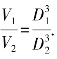换一种形式为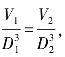也就是说，对于不同的两个球，球体积与其直径的立方之比是相等的，这就意味着对于任意一个球，球的体积与球的直径的立方之比也是一个常数，即存在一个常数m，使得，即V=mD3，阿基米德证明了命题“任一球体的体积等于底面积为球体最大圆面积和高为球半径的圆锥体积的4倍”，如图1-2，用符号语言表示即.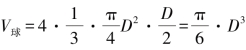

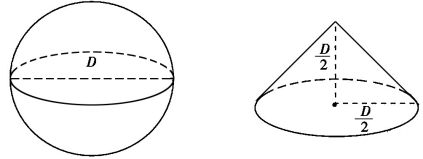
图1-2

那么，对于圆周长、圆面积和球体积这三个不同维数的问题，通过定义圆周率π这样一个概念，使得三个常数（C=πD，S=kD2，V=mD3）都建立在π的基础上，显示了它们之间惊人的统一.我们从小学开始，直到现在，知道了圆周长、圆面积和球体积公式，背它们，用它们，但仅此而已，并没有在思想上就周长、面积和体积形成一个系统的认识.

有了圆周率π这个概念，根据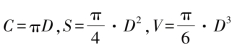，就可以把圆周长、圆面积和球体积的测量问题都转化为直径的测量问题.

接下来我们考虑怎样能得到π的值.当然，古人是通过测量来解决问题的，为了做这个讲座，我也亲手试验了一下，我在办公室看了看，到处都是圆啊！

办公室里的圆周率

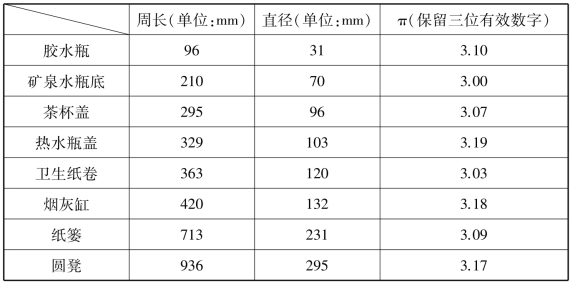
从表中可看出，测量有很大的局限性.用我们最常见的小卷尺测量，可以精确到1mm，但若希望π的值精确到3.142，则需要圆的直径达到10m.而要想得到更精确的值，就需要更大的圆，你还要考虑到圆的平面是否足够平，画的圆是否足够圆，测量工具本身是否规则，测量的人是否认真，等等.

到公元前4世纪，理性的希腊人开始进行深层次的思考，他们对通过测量得出的圆周率的值不感兴趣，开始探讨在理论上如何求得圆周率的值.（顺便说一下，古希腊人崇尚理性，追求知识的理论体系，把数学看作一门“学”；而我们古代中国人崇尚应用，把数学看作一种“术”，中国古代数学著作大多通过应用实例来阐述数学知识，这不利于上升到理论，这可能正是古希腊有《几何原本》，我们有《九章算术》的原因吧）

测量圆周最简单的方法是用细绳紧贴着圆的轮廓绕一圈，在起、终点做好记号再拉直，用尺子测出绳子的长度，阿基米德深知实验操作的局限性，但这种最原始的“化曲为直”的方法也许提示了他，公元前3世纪，阿基米德在《圆的度量》一书中通过作圆的内接和外切正多边形，从内、外两个方向用正多边形（直）来逼近圆周（曲），首次给出了π的上、下界估计.

用圆内接正多边形的周长（直）来替代圆周长（曲），显然有误差，但阿基米德通过不断增加边数，逐步减少误差，不断接近，直至无限接近.

我们从正六边形开始，如图1-3.假定圆的半径为1个单位长度，当边数n=6时，

.

现在我们清楚了，圣经中的“3”和中国古代“周三径一”中的“3”与圆周率的误差是什么概念，从图1-3中可以看出，用正六边形ABCDEF的周长代替圆的周长，误差是明显的.设想做一个正六边形的轮子，要滚起来还不是那么容易呢.

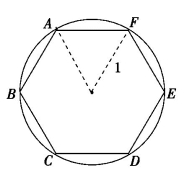
图1-3

为了得到更精确的值，我们在正六边形的基础上加倍.作圆的内接正十二边形，如图1-4.假设圆的半径为1，那么.

我们有，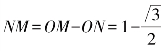

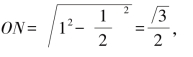
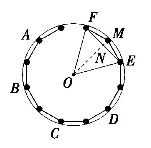
图1-4

从而.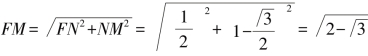

这样，圆内接正十二边形的周长就是，而圆的直径为2，那么，圆周率的值为，化成小数约为3.105828…

显然，正十二边形的周长与圆周的接近程度高于正六边形，若不断地加倍，继续画圆的正二十四边形、正四十八边形、正九十六边形就会不断地提高精确度.

阿基米德不会逐个地计算，他发现了圆内接正n边形的边长an与圆内接正2n边形的边长a2n之间的关系.

如图1-5，设AB=an，CB=a2n，若圆半径为1个单位长度，则

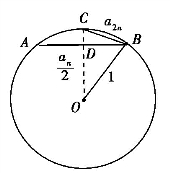
图1-5

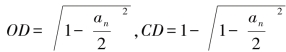，这样

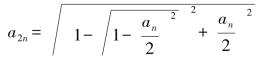，化简得

阿基米德从正六边形a6=1开始，代入（1）即可得正十二边形的边长a12=，

把它代回到方程（1）中，再化简可得，

重复这一过程，，

……

通过不断加倍作圆内接正多边形，从圆内部用正多边形逐步逼近圆周，就可以得到越来越精确的圆周率的值，阿基米德不满足于此.另一方面，他又通过作圆的外切正多边形，从圆外部逐步逼近圆周，这类似于我们在解决不等式问题时用的“两边夹”的方法，这样就从两个不同的方向把圆周率锁定在一个想要有多精确就有多精确的范围内.

那么，要做正多少边形才够呢？阿基米德认为，n=96就足够了（做一个正九十六边形的轮子，那滚起来就是圆啊）.阿基米德用内接和外切正九十六边形的周长从两个方向逼近圆周长，得出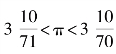，化成小数就是3.140845＜π＜3.142857.

阿基米德（古希腊，公元前287年—公元前212年）

我们从小学就知道的π是3.14的由来就在这里.

这是世界上第一个通过数学计算得到圆周率值的方法，阿基米德开创了圆周率π值的科学计算的悠久历史，对后世数学的发展影响深远.阿基米德的思想也可看作近代微积分的萌芽，大家不要小看这个3.14，古代还未出现小数，只能用分数去逐渐逼近方根，我们很难再现这里面艰辛的计算过程，在阿基米德以后的300年中，圆周率的精度从3.14到3.141，只前进了1位.

古希腊数学文明从毕达哥拉斯、欧几里得一路走来，到阿基米德时代达到顶峰.随着阿基米德被罗马士兵的长矛所杀害，亚历山大著名的图书馆被烧毁，以及有着900年历史的雅典柏拉图学园的关闭，繁荣的古希腊文化走到了尽头.公元1世纪至10世纪，欧洲各国相互征战，宗教斗争也愈演愈烈，经历着黑暗的中世纪时期，科学研究和文化交流陷入停滞状态，这时中国和印度的科学却有长足的发展.公元2世纪到8世纪，这两个国家成为世界最重要的数学研究中心，下面简单介绍一下.

1.张衡，由命题“圆周长和它的外切四边形的周长的平方之比等于5比8”（圆的直径为1）得出圆周率等于，显然和圆周率的值有误差，但也许是因为它简单明了，所以，在亚洲各地风行了好一阵子，被誉为“十全十美平方根”.

2.刘徽，运用“割圆术”，算到圆内接正6×29（3072）边形，求出圆周率的值约为3.1416（徽率），刘徽的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”思想与阿基米德不谋而合.

刘徽（约225—295）

3.祖冲之，祖冲之和他的儿子祖暅以圆内接正6×212（24576）边形计算出圆周率的近似值密率）.据说他们使用一种叫算筹的计算工具，但他们到底是如何得到这个值的，也许永远是个谜是最有名的圆周率的近似值，所有分母在10万以内的逼近分数中，以它最为准确和简练，是我国古代数学的最高成就.（1573年，德国数学家奥托重新发现了这个比值，比祖冲之晚了一千年）

4.印度婆罗摩笈多，求出了直径为1的圆内接正十二边形、正二十四边形、正四十八边形和正九十六边形……的周长分别是和……他根据这些结果，大胆地做出一个归纳推理：当正多边形边数增大到趋近于圆时，它的周长会趋近于，后来这个数值就从印度传到欧洲，成了中世纪全球数学界通用的圆周率值（事实上，作为圆周率的逼近值，数列……是收敛的，但它只收敛到，即，达不到.

祖冲之（429—500）

随着欧洲文艺复兴的到来，越来越多的人重新加入计算圆周率的热潮中，其中有三位数学家比较有名.1585年，荷兰数学家安东尼斯利用圆内接和外切正多边形，求出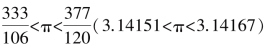，这个结果本来也没什么了不起，但也许是他的运气好，他将两个分数的分子和分母分别相加除以2，竟然得到一千年前祖冲之的.不久，另一位荷兰数学家罗马努斯以超过一亿边的内接正多边形计算出有15位小数的圆周率.最后，德国人鲁道夫利用阿基米德这套在数学界沿用了近两千年的方法，凭着超乎常人的毅力和耐力，他的内接和外切正多边形的边数已超过320亿（6×229），计算出了有35个小数位的圆周率.德意志民族为了纪念他，将圆周率称为“鲁道夫数”.

那么，一个圆内接正多边形要将边数增至多少才算逼近圆呢？其实，阿基米德早就说过，一般情况下，正九十六边形就足够了，哪怕在高端应用中，我们精确到小数点后几位也就足够了.用有10个小数位的圆周率计算地球的周长，其误差不会超过3厘米；用有30个小数位的圆周率计算可见宇宙的周长，其误差小得连最高倍的显微镜都看不出来.可数学家为什么还要不遗余力地往下算呢？他们想干什么？

学生：人类天性喜欢竞赛，若能创吉尼斯纪录，一下就出名了.（笑声）

老师：名利确实是很多事情的原动力，但以名利思想揣测数学家的努力未免有亵渎的味道.数学可分为应用数学和纯数学，真正的数学家对应用数学是不屑一顾的，他们关心的是理论上的东西，比如规律、模式、结构什么的.他们不辞辛苦地进行计算，还是想找到π的规律.

学生：想看看小数是否会出现循环的情况，找到那个循环节.

老师：照这样理解，找到了循环节那意味着什么？

学生：意味着π是一个有理数，这样就求出了π的准确值.

老师：姑且这样理解吧.但要再提高位数，必须在计算方法上进行创新，否则，即使耗费一个人的全部生命，也未必能有长进，不会再有第二个鲁道夫了.

一座高峰，会有不同的人从不同的地方攀登，人们会从不同的方向仰望同一个顶峰.

π的重要性也表现于人们在计算π的过程中不断地发现了新的数学思想方法.

最先跨出这一步的是法国数学家、律师韦达.1579年，韦达效法阿基米德，将圆外切和内接正六边形的边数倍增16次，计算出两个正393216边形的周长，得到圆周率的上限和下限分别为3.1415926537和3.1415926535，韦达的圆周率精确到小数十位，这和鲁道夫比起来算不了什么，但关键的是他有一个新的思想和方法：以无穷乘积表达圆周率.

在讲解韦达伟大的发现之前，我们先需要了解一下弧度制.

是谁发明了弧度制已无从考究，但是，毫无疑问，在角的度量中，使用“弧度”是一个伟大的创举，这可能是劳动人民在长期的生产与生活实践中偶然发现的.

我们在圆周上取与半径长度相等的一段弧，如图1-6，把该弧所对的中心角的大小定义为1弧度，这样，作为角的度量单位

1≈57.30°（1代表1弧度，记为1rad）.

采用弧度制，弧长l和扇形面积S可以简单地表示出来：当中心角为θ弧度时，弧长为θr，扇形面积为.

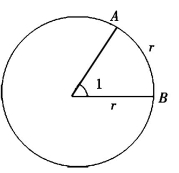
图1-6

弧度制的引入，赋予圆周率π新的含义，利用π表示角度，大大拓展了π的研究空间，使延长π的位数的竞争有了新的途径.

阿基米德之后约1800年，弗兰索瓦·韦达因在某个代数公式上加上了“等等”一词而创造了历史，这个“等等”表示这个公式的过程可以无限地重复下去.当然，希腊人早就知道“无穷”的存在，但他们因为缺少代数工具，“无穷”在两千多年以来一直是一个有争议的课题，是个禁区，人们总是尽可能地回避它.韦达的“等等”突破了这个古老的禁忌，无穷以闪电般的速度登上了数学的舞台中心.

1593年，韦达在《数学问题面面观》一书中，通过对圆的研究，求出了π的一个无穷乘积：

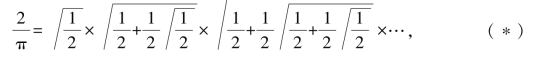
就这个公式来说，我们取

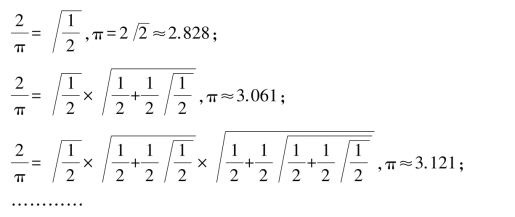
如果继续算下去，就可得到更准确的π的估计值.

对我们高中生来说，考察一下韦达公式的证明是有意思的，大家想一想.

（沉默）

韦达是基于内接于同一圆的正n边形与正2n边形的面积之比，利用几何方法得到了这个等式的，但我们观察式中的结构，应该想到哪个公式呢？

学生：三角函数，半角公式.

老师：对，取，韦达连乘积的第一项为，第二项为，第三项为，这样（*）式可改写为，有谁能证明这个公式？

好，我们不怕复杂，这类题型的化简我们应该见过.

比如化简：cos20°cos40°cos80°.

有了这个铺垫，韦达表达式的证明并不难，我们有：

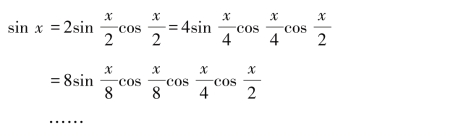
把这个过程重复n次，可以得到

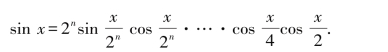
下面是关键的一步，把这个乘积中的项变形为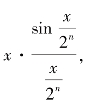则可以得到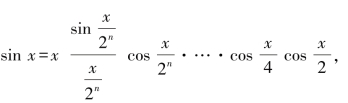

当n→+∞时，，且括号里形如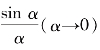的式子趋向于1，于是我们得到

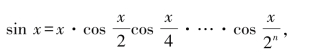
令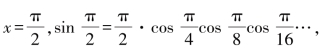

我们知道，，对其余的每一项都利用半角公式计算，就可得到等式

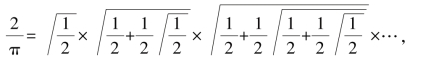
化简为，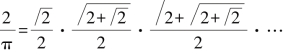

韦达的公式很漂亮，而且简洁、实用，我们只需要用加、乘、除和开平方4种基本运算，全部作用在2上，就能得出π的值，经过九次计算，可得到3.1415914，精确到小数点后第5位，效率很高.

这是人类第一次用无穷乘积叙述一个值，是数学发展史上的重要里程碑.此后就有多种无穷连乘积、无穷连分数、无穷级数等组成的各种表达式，人类开始朝级数和微积分迈进，这些方法为π值的计算开辟了新的途径，很快就突破了用几何方法计算圆周率所创造的纪录.

让我们再来欣赏一个.

英国数学家、物理学家、密码专家沃利斯1655年发现了

这个表达式优美、简洁，我们有

若，则π=4；(www.chuimin.cn)

若；

若；

若；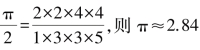

若；

若；

若；

…………

可以看到，随着等式中项的增多，π的值会缓慢地向更准确的值逼近，因这个式子简单，接着算下去也不是什么难事.

除了连乘积以外，级数的表达式也很有效.我们先从学过的知识上看一个例子：求等比数列1，-x2，x4…的和，我们有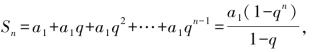当|q|＜1，n→+∞时，，这样即有

两边取积分，得：

令x=1，即有

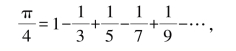
（学生中有人在议论）（停顿，指向一个同学）有什么问题吗？

学生：（*）式是在的情况下得到的，但取积分后老师却令x=1，前后有矛盾.

老师：你反应很快.是的，有点问题，但我们伟大的牛顿在发明微积分时也犯过类似的错误，所以，我们的错误是可原谅的.（笑）

当然，今后大学里我们将学习到，任一连续函数都可以用级数来表示，（*）式也可从函数的幂级数展开导出，我们从等比数列导出，是想让大家在熟悉的层面上来理解它.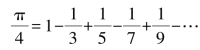这个形式太美了，但美中不足的是它收敛太慢，计算到300个分数，也只能得到小数点后第二位3.14.它是由格雷果里和莱布尼茨各自独立发现的，史称格雷果里-莱布尼茨级数.

（用多媒体列出另一级数）

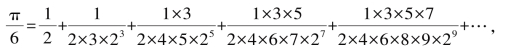
这个级数是牛顿给出的，虽然式子不算简洁，但它很有效.前四项相加就可得出π≈3.14115，前22项相加可精确到小数点后16位，与阿基米德创立的“经典方法”相比，效率大大提高了.

1665年，牛顿为了躲避伦敦的鼠疫，来到乡下钻研科学和数学，他在这段时间有很多辉煌的研究成果.对牛顿这样的大科学家而言，计算圆周率只是一件有趣的小事，但复杂枯燥的数字计算也花了他不少时间：“说来惭愧，虽然我近来没有其他杂事缠身，但仍只计算出了几个小数位.”

牛顿利用他创造的一种强大的新的数学方法——“流数法”（微积分），通过他那天才的构想，这个古老的问题获得了新的生命.

牛顿当然精通解析几何方法，他先作半圆，如图1-7，其圆心位于点，取半径，显然，圆的方程为，展开化简，

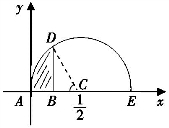
图1-7

即

设B点位于并作BD垂直于半圆的直径AE交上半圆于点D.

准备工作做好后，牛顿开始用两种完全不同的方法，求阴影部分ABD的面积.

1.用几何方法求面积ABD.

显然，

（∠ACD=60°，牛顿的构造使计算变得简捷）

2.用“流数法”求曲边形ABD的面积（牛顿首创），用现代微积分符号表示为

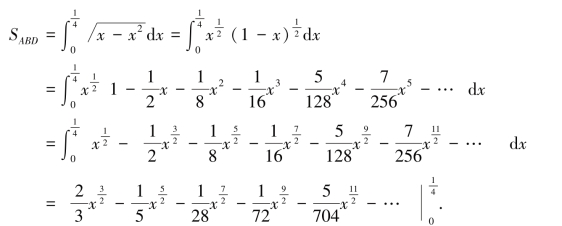
（注意第三步的展开，牛顿用到了他创立的广义二项式定理，这也是牛顿伟大的数学贡献之一，这里我们知道就行了）

牛顿的构造巧妙之处就在于，当我们赋值计算时，展开式中的开方运算消失了，数值计算变得较为简单.

牛顿计算级数展开式中的前9项，得出SABD的近似值为

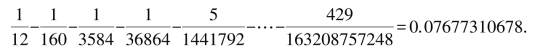
最后，牛顿把用流数法（微积分）计算出的阴影部分面积的近似值与用初等几何方法得出的结果列为方程：

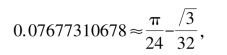
解π，就得到π的近似值π≈3.141592668….

这种方法的惊人之处在于牛顿只用了二项展开式中的前9项，就使π值精确到7位小数，与π相差不足0.000000014，牛顿的近似值比我们在前面讲的韦达或鲁道夫的计算在效率上前进了一大步，这一结果也清楚地表明了他的数学新发现在解决这一古老问题时的显著效能和巨大成功，特别值得一提的是，此时微积分学还没有诞生呢.

历史的车轮滚滚向前，进入18世纪，莱昂纳德·欧拉横空出世，他发现了一系列的π的级数表示：

欧拉用其中一个，只花1小时便得到了π的第20位.

1706年，英国数学家梅钦利用，将π计算到小数点后100位，此后记录迅速突破500位大关.1873年，英国人尚克斯花费15年光阴计算出有707个小数位的圆周率，这是他用纸和笔努力多年的成果，当时的人们将这个成就誉为一项震古烁今的数学发现，尚克斯效仿阿基米德，嘱托将其刻在他墓碑上作为一生的荣誉.可惜的是后来人们发现尚克斯的计算在第527位是错误的，后面180位的计算也白搭了.

我们已经连续讲了两节课了，休息一下如何？

掌声……

好了，我们继续，先简单回顾一下前面讲座的内容，哪位同学来小结一下？

学生：今天老师给我们讲了圆周率的定义和数学家为什么要定义这样一个概念，为我们展示了历史上数学家为计算圆周率所创造的数学方法和付出的辛勤劳动，我现在对圆周率有了一个全新的认识.

老师：什么新的认识？

学生：以前只在公式中运用它，但不了解它，不理解它，现在感觉到心中有π.

老师：很好，还有同学有补充吗？

学生：我没想到圆周率有这么深的内涵和魅力.

老师：更大的魅力还在后面呢.（笑声）

学生：对圆周率的历史了解了更多，发现数学十分复杂但很有趣，原来数学有那么多值得让我们深入思考和学习的地方，老师的讲座扩大了我的视野，还有了一次与高等数学接触的机会，很充实.

老师：比看文艺晚会有意思吧？

（笑声）

老师：是啊，N届春晚小品王带给我们的是什么呢？是知识的盛宴还是美的享受呢？

学生：是娱乐.

老师：在我看来，小品王带给我们的是文字游戏，浅层愉悦和低级趣味，而阿基米德、祖冲之却永远闪耀着智慧的光辉，带领着我们走向光明.

学生：（严肃起来）谢谢老师指点.原先我还以为阿基米德和牛顿都只是纯粹的物理学家，没想到他们数学也这么厉害.

老师：他们还是哲学家呢.

（笑声）

好了，顺便问一下，世界上有很多有名的数学家，他们引领着数学向前发展的方向，当然我们中国古代数学也有非常高的成就，你们知道历史上公认的世界四大数学家吗？指向一学生.

学生：祖冲之、华罗庚、陈景润.

老师：你太爱国了.

（笑声）

老师：还有谁，说一个外国的吧.

学生：对了，还有高斯.

老师：你怎么知道高斯呢？

学生：高斯是数学王子啊！

老师：哦，看来王子的故事还是有名的，一般来说，数学史上公认的世界四大数学家是阿基米德、牛顿、欧拉和高斯.阿基米德被誉为数学之神；欧拉是历史上最多产的数学家，“分析的化身”，18世纪在数学上被称为“欧拉世纪”；高斯是王子；牛顿就不用说了.历史上所有的数学大家都被圆周率的魅力所吸引，他们都亲手计算过π的值，探究过它的存在，解释过它的意义.阿基米德开创了圆周率计算的古典方法；欧拉用级数轻松搞定20位；牛顿发明了微积分，用“流数”来计算π；那么高斯到哪里去了？（笑声）

其实，高斯也曾研究过π，并且利用计算椭圆积分的二次方程式发现了一个新的圆周率的计算方法（二次收敛算则），每经过一次计算，π的有效数字就会倍增，效率很高，但计算实在是过于复杂，数学之王也无能为力，谁能帮帮高斯呢？

这个人在20世纪中叶终于出现了，这个人当然可以被称为世界第五大数学家，这个人是谁呢？（沉默）

老师：计算机！（笑声）

对于20世纪以前的人来说，计算速度快如闪电的电子计算机就像是天方夜谭，但这个梦想在20世纪中叶实现了.1949年，美国数学家弗格森摆脱了恼人的纸和笔，利用早期简易计算机，计算出了有808位的圆周率.

有了电脑的魔力，π的计算突飞猛进，很快就突破了千位、万位、百万位大关，以后的法国人、美国人、日本人开展竞赛，不断创造出新的纪录.1989年，俄罗斯的大卫和葛列格里·楚诺维斯基兄弟突破了10个亿位数，2011年10月16日，日本公司职员近藤茂利用家中电脑，计算到10万亿位，堪称当时的吉尼斯世界纪录，当然，日本人也不要太得意.此时此刻，计算机又不知算到什么地方去了.

学生：找到了那个循环节吗？

老师：当然没有，其实，数学家早就认识到了π不是一个有理数，也就是说圆周率的定义虽然是圆周长与直径之比，但它却不能表示为两个整数之比，正所谓“比非比”，是个“矛盾”的数.1761年，瑞士数学家兰伯特第一个在理论上证明了π是一个无理数，中止了人类将π表示为两个整数比的尝试.

学生：那继续计算下去还有意义吗？

老师：人们热衷于计算圆周率的数值，当然不仅仅是为了创造新的纪录，从计算机计算π来看，这种计算已演变为检验计算机优良程度和计算机程序设计好坏的一种有效方法：如果在计算中得出的数值出了错，这就表示计算机硬件有毛病或软件设计有问题，需要进行更新.对电脑而言，最大的挑战就是计算圆周率——它就像电脑的心电图一样.

当然，对数学而言，数学家用计算机计算π，是想研究π的位数是否有它独特的规律，希望能通过更多的位数看得更远，以找出一些蛛丝马迹.正如楚诺维斯基兄弟说的，我们正在找寻一些规则，一些能凸显出圆周率和其他数值不同之处的规则.这就像用作品文法结构来分析作家，如果有个俄文句子拖了一整页，却没有一个逗点，它一定出自托尔斯泰的手笔.如果有人从圆周率中任意连续抽出100万个小数位数，你是否能看出它们来自圆周率？数学家寻找的是一个特定的模式.

从圆周率第700100位起，连续出现了7个3，从3204765位起又连续出现了7个3；π的前100万小数位包括了99959个0，99758个1，100026个2，100229个3，100230个4，100359个5，99548个6，99800个7，99985个8以及100106个9，各个数字出现的频率接近0.1.回到前面，英国数学家尚克斯以π的707位闻名于世，很长一段时间，人们对他的这一结果深信不疑.1944年，弗格森对尚克斯的707位数中的各个数码出现的次数与频率进行统计，统计表明，各个数码出现的频率有的与0.1相差很大，弗格森因而怀疑尚克斯的计算有误，于是他重新检验，用了整整一年的时间，终于确认尚克斯的π值只有前527位是正确的.

圆周率各位数字是否成正态分布？0123456789，9876543210等数字串会出现在圆周率中吗？像这样的一些问题，显然不是电脑能解决的，它是个理论问题，要找到答案，还是要靠高深的数学功力，而不能指望电脑.目前有很多人认为电脑无所不能，这类问题的存在或许能点醒他们.

圆周率独有的魅力，让人忍不住要多看几眼，它的数字排列完全不按章法，没有任何规律，然而，从数学的观点来看，这正意味着它包含了所有的规律.

美国作家霍夫斯塔德的《哥德尔、埃歇尔、巴哈——集异壁之大成》是一本奇特的科普名作，作者用一种非常规的方式来表述科学思想，其中有一段关于圆周率的对话，大家一起来欣赏一下.

沙维亚提：现在给你两个数列，78539816339744830961566081…，和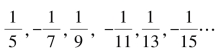，请问，你知道第一个数列接下来会出现的数字吗？

辛浦里修：我不知道.它像是一串随机数学，没有任何规则可循.

辛维亚提：第二个数列呢？

辛浦里修：很简单，一定是.

沙维亚提：对.但你知道吗，第一个数列也有它的规则，而且和第二个数列的规则一模一样.

辛浦里修：怎么可能？

沙维亚提：真的是这样.将第二个数列加总化成十进制小数，就可得到第一个数列.它的值为.

辛浦里修：你的数学戏法还真多，但这和抽象与现实又有什么关系？

沙维亚提：它和抽象的关系非常明显.乍看之下，第一个数列显得毫无规则；但一旦你能从这堆乱数分析出一个简单的结构，便能找出它的规则.

我们就是靠这个方法发现自然规律的.大自然中充斥着看似杂乱无章的现象，但人类总能从其中挑出一些别具意义的现象，将它们抽离出俗世表象的层面，提升到概念的境界.如此一来，就能凸显出这些现象真正的结构.

（注：沙维亚提和辛浦里修为伽利略《两种新科学对话录》的主角.）

有人别出心裁，用其他进制来表示π（如二进制、五进制、十二进制），试图看看有什么规律，结果也是令人失望的；还有人把圆周率的数字转换成音符，谱写圆周率之歌，想听听天籁之音是如何的美妙，初听起来无法听出任何旋律，但一直听下，似乎又好像有些旋律.

圆周率作为一个几何概念，经常出其不意地出现在其他数学分支中，一个比较有名的例子是，数学史上关于级数的求和，这是一个令人头疼的问题，难倒了很多的数学家，欧拉通过巧妙的方法求出了这个和，π出人意料地出现在这里，它的值竟然是.更令人惊奇的是，数学家布丰通过投针实验就可得到π的值，这不但为圆周率研究开辟了一条新路，并逐渐发展成为一种新方法（统计实验法），统计学中的正态分布曲线为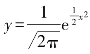，π恒定其中.

圆周率俨然是数学这出戏的主要角色，这出戏已经在广阔的大地上呈现了几千年，π就好像一个有高度威望、交游甚广的个体，它到处抛头露面，与许多别的数学对象有着千丝万缕的联系，令你好奇，给你惊喜.

圆周率不仅大量存在于数学的各个分支中，同时也广泛存在于其他自然科学和艺术领域等范畴里，甚至在声波和海浪的节奏中，也隐藏着圆周率的身影.如在河床中，河流有一种走出更多的环形路径的倾向，因为即使是最细微的弯曲都会使外侧的水流变快，但这反过来又对河岸造成更大的侵蚀和更急剧的转弯，大自然中各种因素的平衡最终会使河流的走向成自然态，奇妙的是河流从源头到出口之间的实际长度与直线距离之比的平均值为π.

π作为自然界中最重要的普适常数，越来越多的人认识到，探索圆周率就像探索宇宙，如果我们能更多地了解这个数值，如果能找出这一长串数字的规律性或认识到圆周率与自然事物间的关联，那么我们对于宇宙的数学和物理性就会有更进一步的认识.

李商隐有诗云：此情可待成追忆，只是当时已惘然.身处其中，我们看不清事态的发展，不明白上天这么安排的意义，不知命运将载我们驶向何方.我们只能由着当时的场景，由着自己浅显的判断随波逐流，若干年，一切都尘埃落定，回忆过往，才惊叹命运早已给出暗示，关键时刻，它都给出了指引，只是当时我们走得太匆忙，没看见，或者我们眼神不够清澈，没看清.π就是一本这样的“书”.

它一直不循环，一直不间断，一直在继续，这一串小数中包含的每一段都是不同的数字，你的生日，手机开机密码，身份证号码，都会出现在这串数字里.如果你把这些数字换成字母，1是a，2是b……24是x，25是y，26是z，你就能够从中找到你上学时学过的每一个单词，你的初恋的名字，你所说所做的一切，你全部的人生故事，这个世界无尽的可能性，都藏在这个非凡的数里.但它不是先知，不会预先告诉，它静静地在那，等一切结束，等谜底揭开，你才恍然惊悟，原来是这样啊.它是一个超强的先知，早已洞悉一切，只是混沌行走的我们无法看透它的预警.

美国作家普利斯顿在《圆周率的山》中有一句话：“圆周率有玄机吗？”这个问题和“死后有来生吗？”一样，也许你死后就知道了.

下面我们来谈一个比较轻松的话题，有谁能背诵圆周率？

学生：3.14159.

学生：3.1415926至3.1415927之间.

学生：3.1415926535897932384626.（鼓掌）

老师：你是怎样记住的？

学生：我是背了一首诗——山巅一寺一壶酒，尔乐苦煞吾，把酒吃，酒杀汝，杀不死，乐而乐.

老师：可能还有同学也背过这首诗，可记住22位小数，这是用中文谐音的方法来记的，背诵圆周率通常有两个方法，一是将数字分组（5或6个一组），分组后经过一番简化，找到它浑然天成的节奏，然后用独特的韵律朗诵，就像和尚念经似的.1987年日本人友良荻秋将π的数值背到了4万位；我国西北农林科技大学硕士吕超用24小时零4分，背到67890位，显示出人脑记忆的惊人潜力.

另一种方法是所谓的字长记忆法，即以每个单词的字母个数代表圆周率的一个位数，选用适当的单词组成一个有意义的文句，便于记忆，为大家所喜爱.如

英语：HowIwishIcouldcalculatepi　嗨，我好想算出圆周率（3.141592），

或长一点的文句：

See，Ihavearhyme，看，我作了一首诗，

Assistingmyfeeblebrain，以增强我的记忆力，

Itstasksoft-timesresisting.　背一些难记的东西.（3.141592653589）

好了，该和圆周率告别了.最后，有一个奇思妙想与大家分享一下，有谁知道彩票吗？

学生：知道，有双色球，还有超级大乐透，七星彩什么的，好多种.

老师：你怎么知道？

学生：到处都是彩票销售点，我外公每期都买双色球.

老师：你赞成外公买彩票吗？

学生：不赞成.

老师：为什么？

学生：因为各种彩票中奖概率可算出来，太小了，根据概率原理，小概率事件在一次实验中几乎不可能发生.

老师：这么说来，你外公和那些天天在彩票站忙乎的人，那些煞有介事画彩票走势的人.都是白忙乎了？

学生：基本上是白忙乎.

老师：告诉大家一个秘密，一天我在散步的时候，突然灵机一动：想到圆周率作为自然界的一个普适常数，它一定会出现在彩票中，从此之后我就用31415926535……去买彩票，虽然目前为止还没中到什么大奖，但我坚信圆周率一定会出现的，我有这样一个信念，所以会一直用圆周率买下去，也许有一天就出彩了.回去告诉你外公好了，跟着老师买，希望在前方.（笑声）

附录：圆周率年表

公元前2000年：埃及人认为

公元前1100年：中国人将3当成π

公元前550年：圣经没有明讲，却暗示π=3

公元前430年：安提丰和布赖森提出穷竭法

公元前3世纪：阿基米德用正九十六边形计算出

263年：刘徽求出

450年：祖冲之求出

650年：婆罗门笈多求出

1593年：韦达首次以无穷乘积描述圆周率

1610年：德国鲁道夫计算出35位小数的圆周率

1666年：牛顿发明微积分，并计算出有16位小数的圆周率

1706年：梅钦计算出有100位小数的圆周率，琼斯首次用符号π代表圆周率

1713年：清朝的康熙皇帝钦订《数理精蕴》，其中记载了有19个位数的圆周率

1748年：欧拉发表《无穷小分析导论》，书中记载了欧拉定理和很多计算π的级数

1761年：兰伯特证明π是无理数

1873年：尚克斯发表有707位小数的圆周率

1882年：林德曼证明π是超越数

1947年：弗格森花了1年的时间，用早期计算机计算出π的808位小数

1989年：楚诺维斯基兄弟计算出4.8亿位小数，安正金田计算出5.36亿位，楚氏兄弟计算出10亿位

2011年：近藤茂，计算出10万亿位