通常,我们把通过对具体的个别事物进行观测所得到的具有时间和空间分布的信息称为模式,而把模式所属的类别或同一类中模式的总体称为模式类,简称为类。模式识别技术的目标是模拟人的识别方法,但这一点是极不容易做到的,目前模式识别的一些理论方法仍停留在理论研究阶段。当今时代科技发展的重要趋势之一是智能化,模式识别是人工智能的一个分支。......
2023-11-19
小波变换的概念是法国工程师J.Morlet 和A.Grossmann 在1974年提出的。1986年数学家Y.Meyer 构造出第一个真正的小波基,并与S.Mallat 合作建立了构造小波基的方法及其多尺度分析之后,小波分析才开始蓬勃发展起来,比利时女数学家I.Daubechies 撰写的《小波十讲》 (Ten Lectures on Wavelets)对小波的普及起了重要的推动作用。小波分析是调和与分析这一数学领域半个世纪以来众多科学家的工作结晶,小波分析优于传统傅里叶变换的地方是,它在时(空)域和小波域同时具有良好的局部化性能,并通过伸缩和平移运算对信号进行多尺度细化分析(Multiscale Analysis),从而解决了傅里叶变换不能解决的许多问题,被誉为“数学显微镜”。因此,小波变换在信号分析和图像处理领域获得了广泛的应用。
小波的数学定义为:
对于函数ψ(x)∈L2(R),若满足
则这个函数就可以是一个基本小波。对小波进行平移、伸缩生成的函数族
构成一组小波基,其中a 是尺度伸缩参数,b 是位置平移参数。
用上述小波基对函数f(x)∈L2(R)进行的连续小波变换定义为
小波变换实质上是原始信号与经过尺度伸缩后的小波函数族的相关运算,运算结果称为小波系数。通过调整尺度因子,可以得到具有不同时频宽度的小波以匹配原始信号的不同位置,达到对信号的局部分析的目的。式(2-92)的卷积形式为
(Wψf)(b,a)=f*ψb,a
可见,从滤波器的观点出发,小波变换又可看成是用一组不同尺度的小波滤波器对原始信号进行的滤波运算,从而将信号分解到一系列频带上。(www.chuimin.cn)
由小波变换的结果可以重构原始信号,小波变换的重构公式为
式中,
上述过程必须满足完全重构条件
同时,Ψ (x)还应满足窗函数的约束条件
因此,为了满足完全重构条件,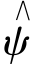 (ω)在原点必须等于零,即
(ω)在原点必须等于零,即
在对信号f(x)连续小波变换(Wψf)(b,a)中,参数a,b 的值域为整个实轴。
对连续小波变换的小波基的伸缩尺度a 二进离散化,同时也对卷积的平移参数b 离散化,取![]() ;就可得到一类对时间-尺度都离散化了的小波变换,称为二进小波变换:
;就可得到一类对时间-尺度都离散化了的小波变换,称为二进小波变换:
有关基于计算机数字图像处理技术木材表面纹理特征提取和分类识别方法的文章

通常,我们把通过对具体的个别事物进行观测所得到的具有时间和空间分布的信息称为模式,而把模式所属的类别或同一类中模式的总体称为模式类,简称为类。模式识别技术的目标是模拟人的识别方法,但这一点是极不容易做到的,目前模式识别的一些理论方法仍停留在理论研究阶段。当今时代科技发展的重要趋势之一是智能化,模式识别是人工智能的一个分支。......
2023-11-19

随着计算机技术的飞速发展,国内外学者将计算机数字图像处理技术引入木材学领域,为解决这一难题提供了新的思路。计算机数字图像处理主要包括以下几项内容:几何处理、算术处理、图像增强、图像复原、图像重建、图像编码、模式识别、图像理解等。......
2023-11-19

在FMDTD的驱动下,实现综采工作面生产要素管理、生产过程预仿真与实时控制等在PFM,VFM,FMDMS的迭代运行,从而在满足特定地质条件的约束前提下,达到综采工作面生产系统配置和装备协同安全高效开采的目的。......
2023-10-30

针对常见特征选择方法的不直接性,我们将子集评价函数直接选为分类器的识别率,提出一种基于模拟退火算法与最近邻分类器识别率的特征选择方法。因此,我们最终选用最近邻分类器识别率作为评价准则。模拟退火算法中最常用的是2变换法和3 变换法,这两种方法有着各自独特的优越性,我们将这两种方法随机交替使用获得了较好的效果。......
2023-11-19

图10-7 一维小波分解简图一维小波的信号除噪是小波分析的重要应用之一。图10-9 一维信号小波除噪Simulink模型对信号除噪的目的就是抑制信号中的噪声部分,从而在信号中恢复有用信号。图10-11 二维图像信号小波除噪图10-11 二维图像信号小波除噪......
2023-06-23

目前,纹理在许多领域有着广泛的应用,如遥感图像分析、医学图像分析、缺陷检测、基于生物特征的身份鉴定、文档分割、目标识别以及图像检索等方面。目前,纹理分析被应用在遥感图像分析的领域有遥感图像目标识别、遥感图像地形分类和卫星遥感图像云类识别等。Landeweerd 和Gelsema 利用纹理的一阶和二阶统计来检测白血球的各种形态和它们的畸变,用于检测病情。......
2023-11-19

所谓计算机数字图像处理,就是利用计算机或实时硬件对计算机数字图像进行系列操作,从而获得某种预期结果的技术。近十几年来,计算机数字图像处理技术的发展更为深入、广泛和迅速,这主要是因为各个领域对其提出了越来越高的要求以及相关学科的飞速发展。现在人们已充分认识到计算机数字图像处理技术是认识世界、改造世界的重要手段之一。......
2023-11-19

小波变换是迄今为止最有效的信号分析方法,它在时频平面上,同时具有很好的时间和频率分辨能力,能够分辨多尺度特征信号的细节部分。小波变换在信号处理、计算机视觉等领域发挥越来越大的作用。小波分析兼具处理空间和频率信息的特点。小波分析在弧焊图像降噪、边缘特征信息提取、视觉跟踪等方面具有重大的潜在优势。......
2023-06-26
相关推荐