基于计算机图像处理的木材纹理特征提取及分类方法

2023-11-19 理论教育版权反馈

【摘要】：针对常见特征选择方法的不直接性，我们将子集评价函数直接选为分类器的识别率，提出一种基于模拟退火算法与最近邻分类器识别率的特征选择方法。因此，我们最终选用最近邻分类器识别率作为评价准则。模拟退火算法中最常用的是2变换法和3 变换法，这两种方法有着各自独特的优越性，我们将这两种方法随机交替使用获得了较好的效果。

针对常见特征选择方法的不直接性，我们将子集评价函数直接选为分类器的识别率，提出一种基于模拟退火算法与最近邻分类器识别率的特征选择方法（The Feature Selection Method Based on Simulated Annealing Algorithm and the Recognition Rate of 1－NN Classifier，SNFS）。该算法具有较强的参数选择能力，能在多项式时间内找出问题的近似最优解。

1.个体编码

在遗传算法中，代表染色体的二进制位串具有表达简单、操作方便、可代表较广范围的不同信息等优点。因此，我们采用二进制编码方式对个体（子集）进行编码。若原始特征有10 个，则个体的长度L＝10，个体的每一个基因对应相应次序的特征。当个体中的某个基因为“1”时，表示该基因所对应的特征项被选用，而为“0”时，则表示未被选中。例如，“1110010100”表示只有第1，2，3，6，8 个特征被选用。

2.评价准则（评价函数或代价函数）

特征选择的最终目的是找出分类能力最强的特征组合，因此，需要一个评价准则来度量特征组合的分类能力。特征选择的度量总体上可以分为3 类：准确性度量、一致性度量和经典度量。一般来说，前者要优于后两者，但相应的时间复杂度也要高。分类器识别率是准确性度量，是最直观的评价准则。而最近邻分类器是最经典、最常见的非参数统计模式识别方法，只要合理选择分类器标准样本数目，并结合快速算法，就能将其耗用的CPU 时间控制在很小的范围内，并且在很大程度上能够避免分类器设计对识别率的影响，进而能更好地反映特征子集的性能。因此，我们最终选用最近邻分类器识别率作为评价准则。

3.邻域结构

一种新解产生法则对应一种特定的邻域结构。模拟退火算法中最常用的是2变换法和3 变换法，这两种方法有着各自独特的优越性，我们将这两种方法随机交替使用获得了较好的效果。其中，2 变换法和3 变换法具体实现如下：

（1）2 变换法。

任选访问的序号u 和v，逆转u 和v 及其之间的访问顺序，此时产生的新解为（设u<v）

（2）3 变换法。

任选访问的序号u，v 和w，将u 和v 之间元素插到w 之后访问，此时产生的新解为（设u≤v<w）

4.冷却进度表

（1）初始温度t0的选择。

Kirkpatrick 等在1982年提出了确定t0值的经验法则，Johnson 等人对这个经验法则进一步深化提出，通过计算若干次随机变换目标函数平均增量的方法来确定t0值，具体见式（2－11）和式（2－12）。

式中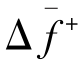， pagenumber_ebook=55,pagenumber_book=48 表示上述平均增量。我们采用的具体实现方法如下：

假定对控制参数的某个确定值t 产生一个m 个尝试的序列，并设m1和m2分别是其中目标函数减小和增大的变换数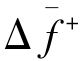， pagenumber_ebook=55,pagenumber_book=48 是m2次目标函数增大变换的平均增量，则接受率χ0可以用式（2－13）近似计算。

由式（2－13）可得

只要将式（2－14）中的χ 设定为初始接受率χ0，就能求出相应的初始温度t0。(www.chuimin.cn)

（2）衰减函数的选择。

为避免算法进程产生过长的Markov 链，控制参数tk的衰减量以小为宜，这样可以保证两个相继值tk和tk＋1上的平稳分布是相互逼近的。如果在tk值上达到准平衡，那么可以期望在tk衰减为tk＋1以后，只需进行少量的变换就可以恢复tk＋1值上的准平衡，这样就可以选取较短长度的Markov 链来缩减CPU 时间，但tk较小的衰减量可能导致算法进程迭代次数的增加，耗用更多的CPU 时间。因此，折中考虑，选用Kirkpatrick 等提出的控制参数衰减函数，见式（2－15）

式中，k＝0，1，2，…；a＝0.95。

（3）Markov 链长度Lk的选择。

Markov 链的长度选取原则是，在控制参数t 的衰减函数已经选定的前提下，Lk应选得在控制参数t 的每一个取值上都能恢复准平衡。其中，在控制参数的每一取值上恢复准平衡需要进行的变换数可以通过至少应接受的变换数来推算。但由于变换的接受率随控制参数值的递减而减小，接受固定数量的变换需进行的变换数随之增多，最终在tk→0 时，Lk→∞。因此，针对式（2－15）选择的衰减函数，我们选用固定的常量L 来限定的Lk值，并取L＝100n，其中n 是问题的规模。

（4）停止准则的选择。

模拟退火算法收敛于最优集是随控制参数t 值的缓缓减小而渐近进行的，只有在控制参数终值tf充分小时，才能得出高质量的解。因此，停止准则一般选择为tf<δ，其中δ 是个非常小的正数，但这样不能保证最终解的质量。为了兼顾最终解质量和算法的时间复杂度，我们选用的停止准则为：在相继的s 个Markov 链中，代价函数值无变化。这里将s 定义为最优解质量等级，考虑到算法的时间复杂度，一般情况下取s≤5。如需要提高最优解的质量，只需增大s 取值，默认情况下取s＝1。

5.有记忆的模拟退火算法

模拟退火算法的搜索过程是随机的，且当t 较大时可以接受部分恶化解，随着t 的衰减，恶化解被接受的概率逐渐减小为0。但在某些当前解达到最优解时必须经过恶化的“山脊”，因此，前文中的停止准则不能完全确保解的质量。为解决以上问题，我们在算法中增加一个记忆器，使之能够记住搜索过程中的最好解，当退火过程结束后，将所得的最终解与记忆器中解比较作为最优解，这样确保了算法中最优解的质量。

SNFS 算法的伪代码如下：

（1）设定最优解维数范围Scale 和质量等级Quality。例如，若设定Scale∈[3，8] 和Quality＝2，表示选择的特征组合中参数个数属于[3，8]，停止准则s＝2。

（2）根据Scale 随机产生初始解Y0，并在记忆器中以及最终解变量中保存初始解Y0值及其评价函数值。产生Y0具体作法如下：Scale 最小值表示Y0中“1”的个数，Y0中其余位置均被“0”覆盖，其中“1”的位置是随机的。

（3）根据前文中所提方法产生新解，并计算新解的评价函数值，然后分别与记忆器中以及最终解变量中的代价函数值进行比较，如果其值大于记忆器中或最终解变量中的评价函数值，则相应地将记忆器中以及最终解变量中的信息被新解的信息替代；否则，按照Metropolis 准则进行。如果接受了恶化解，则在最终解变量中的信息被新解的信息替代，将该步骤循环执行一个Markov 链的长度。

（4）如果在一个Markov 链中，评价函数值没有变化则跳至步骤（5）；否则，按照式（2－15）的衰减函数tk＋1＝tk×0.95 进行衰减，并跳至步骤（3）。

（5）判断是否达到Scale 的最大值，若是，则跳至步骤（6）；否则，保存前一个最优解中“1”的位置不变，然后随机将该解中某一个为“0”位置变为“1”，作为下一个新解，执行步骤（3）产生新解以后的部分。

（6）算法结束，记忆器和最终解变量中的大者就是最优解，其中最优解中“1”所对应特征，即为选择后的特征参数组合。

基于计算机图像处理的木材纹理特征提取及分类方法

相关推荐