高等数学：变力沿直线做功

2023-11-19 理论教育版权反馈

【摘要】：解如图6－25所示建立坐标系.取x为积分变量，x∈［2，8］.图6－25考察区间［x，x＋dx］上的一薄层水，将这薄层水“提到”池口的距离为x，将这层水抽出，克服重力所做的功为于是

设物体在连续的变力F（x）作用下沿x轴由x＝a移动到x＝b时，变力F（x）在［a，b］上所做的功为

例1　设有一弹簧，假定被拉长0.5cm时需用力1N（牛顿），现弹簧在外力的作用下被拉长3cm，求外力所做的功.

解　（如图6－23所示）根据胡克定理，在一定的弹性范围内，将弹簧拉伸（或压缩）所需的力F与伸长量（压缩量）x成正比，即

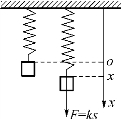
pagenumber_ebook=231,pagenumber_book=220

图6－23

F＝kx　（k＞0为弹性系数）

因为x＝0.005m时，

F＝1N

代入上式得

k＝200N／m

即有

F＝200x

取x为积分变量，积分区间为［0，0.03］，功元素为dW＝F（x）dx＝200xdx.

于是弹簧被拉长了3cm时，由公式（6－7）得外力所做的功为

例2　质量为m的火箭由地面垂直向上发射.试求火箭从地面升空到高为h时克服地球引力所做的功（设地球半径为R，质量为M）.

解　（如图6－24所示）建立坐标系，火箭由地面垂直向上发射时，火箭离地面的距离x是变化的.以x为积分变量，其变化区间为［R，R＋h］，在［R，R＋h］上取代表区间［x，x＋dx］，当火箭从x飞到x＋dx时克服地球引力所做的功元素为

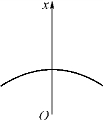
pagenumber_ebook=231,pagenumber_book=220

图6－24(www.chuimin.cn)

所以火箭从地面上升到高为h时克服地球引力所做的功为

又因为r＝R时地球对火箭的引力为mg，于是由

得

故

从上式不难得到，当火箭脱离地球引力即h→∞时克服地球引力所做功的W∞＝mgR.

例3　一个半径为4m，高为8m的倒圆锥形水池，里面有6m深的水，要把池内的水全部抽完，需要做多少功？

解　如图6－25所示建立坐标系.取x为积分变量，x∈［2，8］.

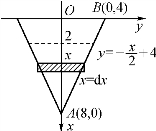
pagenumber_ebook=232,pagenumber_book=221

图6－25

考察区间［x，x＋dx］上的一薄层水，将这薄层水“提到”池口的距离为x，将这层水抽出，克服重力所做的功为

于是