表示常量，用字母x，y，z，t，…......
2023-11-19
高数上册：平面曲线的弧长
【摘要】：平面曲线的长度称为弧长.由于曲线的弧长具有可加性，下面用元素法来讨论平面曲线弧长的计算公式.设曲线弧由直角坐标方程y＝f（x）（a≤x≤b）给出，其中f（x）在［a，b］上具有一阶连续导数，求曲线L的弧长s.如右图6－20所示，取x为积分变量，则积分区间为［a，b］，任取区间［x，x＋dx］［a，b］，由弧微分公式可知弧长元素为图6－20故曲线弧长为若平面曲线L由参数方程给出，x＝φ（x），y＝ψ
平面曲线的长度称为弧长.由于曲线的弧长具有可加性，下面用元素法来讨论平面曲线弧长的计算公式.
设曲线弧由直角坐标方程y＝f（x）（a≤x≤b）给出，其中f（x）在［a，b］上具有一阶连续导数，求曲线L的弧长s.
如右图6－20所示，取x为积分变量，则积分区间为［a，b］，任取区间［x，x＋dx］⊂［a，b］，由弧微分公式可知弧长元素为
图6－20
故曲线弧长为
若平面曲线L由参数方程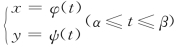
给出，x＝φ（x），y＝ψ（t）在［α，β］上具有连续导数.此时弧微分为
从而所求弧长为
若平面曲线L由极坐标方程ρ＝ρ（θ）（α≤θ≤β）给出，ρ（θ）在［α，β］上具有连续导数.则对应的弧微分为
从而所求弧长为
例12 计算曲线
上相应于x从a到b的一段弧的长度.
解 
从而弧长元素
因此所求弧长为(www.chuimin.cn)
例13 计算摆线x＝a（θ－sinθ），y＝a（1－cosθ）的一拱（0≤θ≤2π）的长度.
解 弧长元素为
由此，所求弧长为
例14 设曲线L的方程为
求曲线L的长度.
解 弧长元素为
由此，所求弧长为
例15 求阿基米德螺线ρ＝aθ（a＞0）相应于θ从0到2π一段的弧长（图6－21）.
图6－21
解 弧长元素为
于是，所求弧长为
有关高等数学 上册的文章
- 详细阅读
-
高数上册：函数图形描绘详细阅读
要比较准确地描绘出一般函数的图形，仅用描点作图是不够的，为了提高作图的准确性，可将前面讨论的函数性态应用到曲线的作图上，即先利用函数的一阶、二阶导数，分析函数的单调性、极值、凹凸性与拐点等整体性态，并求出曲线的渐近线，然后再描点作图，称这种作图的方法为分析作图法.其一般步骤如下：（1）确定f（x）的定义域、间断点，并讨论函数的奇偶性、周期性.（2）在定义区间内求函数f（x）的一阶、二阶导数为零或不......
2023-11-19
-
高数上册：换元积分法详细阅读
有些不定积分难以用凑微分的方法来积分，比如等.但此时若作适当的x＝φ（t）变 换 后会变得容易积分，这种换元积分的方法称为第二类换元积分法，具体叙述如下.定理2设x＝φ（t）有连续的导函数，且φ′（t）≠0，又设F（t）＋C，则有其中φ－1（x）是x＝φ（t）的反函数.证只需证明两个不定积分有相同的原函数即可.因为F（t）是f（φ（t））φ′（t）的原函数，记Φ（x）＝F（φ－1（x）），则即......
2023-11-19
-
弧长控制技术及代表性弧焊电源介绍详细阅读
此种情况下，只能采用电流、电压补偿的方法对电弧能量及弧长加以控制，而传统弧焊电源的控制技术很难满足其要求。图8-10所示为焊接过程弧长数字控制效果图。目前拥有弧长控制功能的代表性弧焊电源有奥地利福尼斯公司生产的数字化TPS4000系列气体保护焊机、日本松下公司生产的YM-500KA1全数字化CO2/MAG焊机等。......
2023-06-30
- 详细阅读
-
高数上册-函数最大最小值详细阅读
解设圆柱形密闭锅炉的底半径为R，高为h，则其表面积S＝2πRh＋2πR2由将它代入上式得由解得唯一的驻点又由于制造固定容积的圆柱形密闭锅炉时，一定存在一个底半径，使锅炉的表面积最小.因此，当时，S在该点取得最小值.此时，相应的高即当圆柱形密闭锅炉的高与底直径都等于时，表面积最小，从而使用料最省.......
2023-11-19
- 详细阅读
-
初等函数连续性-高数上册详细阅读
）时无意义，故x＝kπ（k＝0，±1，±2，…）均为的间断点.当x＝0时，由于故x＝0为f的第一类可去型间断点；当x＝kπ（k＝±1，±2，…）为f的第二类无穷型间断点.......
2023-11-19
相关推荐