定义1若则称函数f(x)为当x→□时的无穷小量,简称无穷小.特别地,若则称数列{xn}是n→∞时的无穷小.例如,由于所以函数是x→∞时的无穷小;由于所以常数0可以看作任意变化过程时的无穷小;由于所以数列是n→∞时的无穷小.应当指出无穷小是对应特殊变化过程时的变量或函数,不能将它与绝对值很小很小的固定常数混为一谈.任何非零常数无论其绝对值多么小,都不是无穷小.由于零的极限是零,所以零是唯一可以作为......
2025-09-30
定义1 设函数f(x)在区间[a,+∞)上连续,任取t>a.如果![]() 存在,则称此极限为函数f(x)在无穷区间[a,+∞)上的反常积分(简称无穷积分),记作
存在,则称此极限为函数f(x)在无穷区间[a,+∞)上的反常积分(简称无穷积分),记作
![]()
这时也称反常积分![]() 收敛;如果上述极限不存在,则称反常积分
收敛;如果上述极限不存在,则称反常积分![]() 发散.
发散.
类似地,可定义函数f(x)在无穷区间(-∞,b]上的反常积分:任取t<b,则
![]()
对于函数f(x)在(-∞,+∞)上的反常积分,可用前面两种无穷积分来定义:
![]()
其中c为任一实数,当且仅当右边两个无穷积分都收敛时![]() 才收敛,否则称无穷积分
才收敛,否则称无穷积分![]() 发散.
发散.
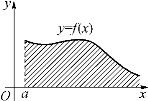
图5-10
![]() 的几何意义是:设f(x)在[a,+∞)上为非负连续函数,若
的几何意义是:设f(x)在[a,+∞)上为非负连续函数,若![]() 收敛,则其值等于图5-10中介于曲线y=f(x)、直线x=a以及x轴之间那一块向右无限延伸的阴影区域的面积
收敛,则其值等于图5-10中介于曲线y=f(x)、直线x=a以及x轴之间那一块向右无限延伸的阴影区域的面积![]() 的几何意义请读者自己给出.
的几何意义请读者自己给出.
为书写简便起见,实际运算中常常省去极限记号,而形式地把∞当成一个“数”,直接利用牛顿-莱布尼茨公式的格式进行计算:(https://www.chuimin.cn)
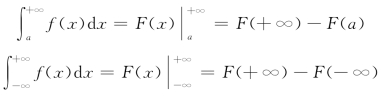
其中F(x)为f(x)的原函数,记号F(±∞)理解为极限运算:F(+∞)=![]() .进而无穷积分的计算也有与定积分相类似的分部积分法与换元积分法.
.进而无穷积分的计算也有与定积分相类似的分部积分法与换元积分法.
例1 讨论![]() 的敛散性.
的敛散性.
解 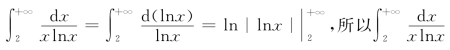 发散.
发散.
例2 计算反常积分![]()
解

例3 计算反常积分![]()
解
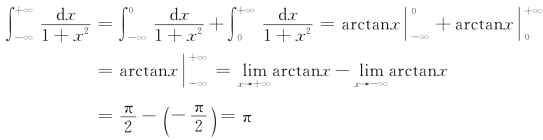
相关文章

定义1若则称函数f(x)为当x→□时的无穷小量,简称无穷小.特别地,若则称数列{xn}是n→∞时的无穷小.例如,由于所以函数是x→∞时的无穷小;由于所以常数0可以看作任意变化过程时的无穷小;由于所以数列是n→∞时的无穷小.应当指出无穷小是对应特殊变化过程时的变量或函数,不能将它与绝对值很小很小的固定常数混为一谈.任何非零常数无论其绝对值多么小,都不是无穷小.由于零的极限是零,所以零是唯一可以作为......
2025-09-30

我们已经知道两个无穷小量的和、差、积仍为无穷小,但两个无穷小量的商的情形就较为复杂,例如下面几个简单的无穷小量的商的极限:从上面三个极限中就看出:虽然当x→0时,x3,x2,x,1-cosx都是无穷小,但它们比值的极限却有着各自不同的情形,分析这些情形产生的原因,发现是由于各个无穷小趋于零的快慢程度不同而造成的.就上面的例子来说,在x→0的过程中,x2→0的速度比x→0要快,x2→0的速度比x3→......
2025-09-30

上节我们在复合函数求导法则的基础上,给出了转化不定积分的重要方法——换元积分法.但有很多积分如等利用换元积分仍然无法积出.本节将在函数乘积的求导公式的基础上,推导出转化不定积分的另一重要方法——分部积分法.设函数u=u(x),v=v(x)具有连续的导数,那么两个函数乘积的求导公式为(uv)′=u′v+uv′移项得uv′=(uv)′-u′v对上式两边积分得或公式(4-2)或(4-3)称为不定积分的分......
2025-09-30

定理1设函数f(x)在[a,b]上连续,函数x=φ(t)满足条件:(1)φ(α)=a,φ(β)=b,且a≤φ(t)≤b.(2)φ(t)在[α,β](或[β,α])上有连续导数.则有公式(5-5)称为定积分的换元公式.证由于f(x)在[a,b]上连续,则存在原函数,在[a,b]上可积.设F′(x)=f(x),则又{F[φ(t)]}′=F′[φ(t)]·φ′(t)=f[φ(t)]·φ′(t),于是......
2025-09-30

两个多项式的商称为有理函数,其中n和m是非负整数,且a0≠0,b0≠0.当n≥m≥1时,称式(4-5)所表示的函数为有理假分式函数;当n<m时,称式(4-5)所表示的函数为有理真分式函数.当f是假分式时,利用多项式的除法,可将它化为一个多项式与一个真分式的和.例如,因此有理函数的积分问题可归结为求真分式的积分问题.1)有理函数的分解定理1设有真分式(4-5)式,若Qm=b0(x-a)α…(x-b)βλ…......
2025-09-30

若函数f(x)≥0,则在几何上表示由曲线y=f(x)、直线x=a和x=b与x轴围成的曲边梯形的面积.当函数f(x)≤0时,由定积分定义知在几何上表示由曲线y=f(x)、直线x=a和x=b与x轴围成的曲边梯形(在x轴下方)的面积的相反数.图5-3一般地,若f(x)在[a,b]上既取得正值又取得负值,则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5-3所示,有由几何意义易知,在......
2025-09-30

性质1设函数f(x)的原函数存在,k为非零常数,则证因为,所以类似可证明不定积分有下列性质.性质2设函数f(x)与g(x)的原函数均存在,则性质2可推广到有限个函数的情形.利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.对于不定积分运算需要指出,虽然每个积分号都含有任意常数,但任意常数之和仍是任意常数,所以遇到几个任意常数时只要写一个任意常数即可.例5求解例6求解积分运......
2025-09-30

定义2若F(x)是f(x)在区间I上的一个原函数,则称F(x)+C为f(x)在区间I上的不定积分,记作即∫f(x)dx=F(x)+C其中C为任意常数,记号“∫”称为积分号,f(x)称为被积函数,f(x)dx称为被积表达式,x称为积分变量.由定义2可知,求的关键就是求出f(x)的一个原函数,不定积分与原函数是总体与个体的关系.由此,本节开头所举的两个例子可写作从不定积分的定义即可知下述关系:或又由......
2025-09-30
相关推荐