首页理论教育高等数学第一册牛顿-莱布尼茨公式解析

高等数学第一册牛顿-莱布尼茨公式解析

2023-11-19 理论教育版权反馈

【摘要】：解首先计算开始加速到匀速行驶所需的时间，即匀加速运动从v0＝0到v＝180km／h所需的时间：由匀加速运动的速度v＝v0＋at＝0.5t＝50，得t＝100s.因此火车开始匀速行驶的地方到车站的距离应为：例9计算解被积函数含有绝对值符号，应先去掉绝对值符号后再积分，即分段积分.

定理3（微积分基本定理）　设f（x）在区间［a，b］上连续，F（x）是f（x）在［a，b］上的一个原函数，则

证　由题设可知F（x）是f（x）在［a，b］上的原函数，由定理1可知，Φ（x）＝也是f（x）在［a，b］上的一个原函数，因此

在上式中，令x＝a，得C＝－F（a），再将之代入上式得

令x＝b，并把积分变量t换成x，便得到

为了方便，通常把F（b）－F（a）记为于是式（5－4）可写成

公式（5－4）称为牛顿－莱布尼茨公式.该公式进一步揭示了定积分与不定积分这两个概念之间的内在联系，从此便有了计算定积分的一般方法，即将定积分的值转化为原函数的增量，而原函数的求法已经在上一章“不定积分”中介绍了.这一公式的发现是积分学发展史的一个飞跃.因此，定理3也称为微积分的基本定理.

例1　已知

解　由式（5－3）可得

例2　已知

解　函数是由与u＝x2复合而成的，利用复合函数的链式法则，有

在f（x）连续且u（x），v（x）可导的条件下，利用定理1及函数的导数公式可得下述变限积分函数的导数公式：

（1）设

（2）设

（3）设

例3　已知

解　　

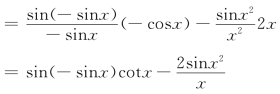
pagenumber_ebook=205,pagenumber_book=194

在讨论极限、函数性态、中值定理等导数应用问题时，我们也会经常碰到变限积分函数.(www.chuimin.cn)

例4　求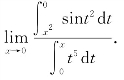 pagenumber_ebook=205,pagenumber_book=194

解　这是一个型的未定式，应用洛必达法则，有

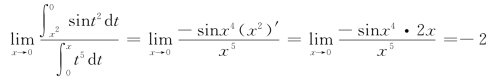
pagenumber_ebook=205,pagenumber_book=194

例5　设函数求F（x）的单调区间.

解　令F′（x）＜0得解之得即为F（x）的单调减区间.

令F′（x）＞0得，解之得即为F（x）的单调增区间.

例6　计算 pagenumber_ebook=205,pagenumber_book=194

解　由于arcsinx是的一个原函数，所以有

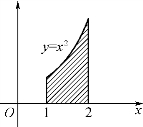
pagenumber_ebook=205,pagenumber_book=194

图5－7

例7　求由y＝x2，x＝1，x＝2及x轴所围图形的面积（图5－7）.

解　由定积分定义知，所围图形的面积

例8　一列动车从A站以a＝0.5m／s2的加速度匀加速启动，当速度达到180km／h时开始匀速行驶，问火车需要离开站台多少米才可使火车匀速行驶？

解　首先计算开始加速到匀速行驶所需的时间，即匀加速运动从v0＝0到v（t）＝180km／h所需的时间：

由匀加速运动的速度v（t）＝v0＋at＝0.5t＝50，得t＝100s.

因此火车开始匀速行驶的地方到车站的距离应为：

例9　计算

解　被积函数含有绝对值符号，应先去掉绝对值符号后再积分，即分段积分.

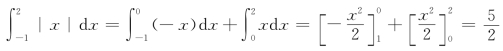
pagenumber_ebook=206,pagenumber_book=195