首页理论教育高等数学上册：变上限积分函数及导数探究

高等数学上册：变上限积分函数及导数探究

2023-11-19 理论教育版权反馈

【摘要】：设y＝f（x）在［a，b］上连续，且x0∈［a，b］.设Φ（x0）表示由曲线y＝f（x）、x轴、直线x＝a和x＝x0所围平面图形面积的代数和.显然，由定积分的概念可知Φ（x0）一定存在，且其大小只与x0有关，与积分变量x无关.为明确起见，用t做积分变量，将x0换成x，从而给出积分函数的定义.定义1设函数f（x）在［a，b］上可积，x∈［a，b］，则函数是上限变量x的函数，称为变上限积分函数，记作

设y＝f（x）在［a，b］上连续，且x0∈［a，b］.设Φ（x0）表示由曲线y＝f（x）、x轴、直线x＝a和x＝x0所围平面图形面积的代数和.显然，由定积分的概念可知Φ（x0）一定存在，且其大小只与x0有关，与积分变量x无关.为明确起见，用t做积分变量，将x0换成x，从而给出积分函数的定义.

定义1　设函数f（x）在［a，b］上可积，x∈［a，b］，则函数是上限变量x的函数，称为变上限积分函数，记作Φ（x），即

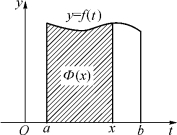
pagenumber_ebook=202,pagenumber_book=191

图5－5

必须指出，变上限积分函数是关于上限x的函数.对取定的x，它有确定的值（定积分的值），与积分变量t无关.几何上，变上限积分函数Φ（x）表示如图5－5中阴影部分的面积.它具有如下的重要性质.

定理1　设函数y＝f（x）在区间［a，b］上连续，则变上限积分函数Φ（x）＝在［a，b］上可导，且

证　设∀x∈［a，b］及增量Δx（x＋Δx∈［a，b］），则函数Φ（x）在点x＋Δx的函数值为

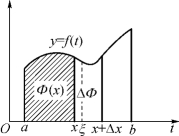
pagenumber_ebook=203,pagenumber_book=192

图5－6(www.chuimin.cn)

相应的增量ΔΦ（图5－6）为

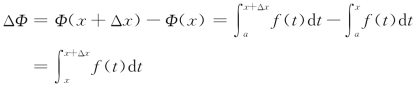
pagenumber_ebook=203,pagenumber_book=192

由估值定理有

ymΔx≤ΔΦ≤yMΔx（ym，yM为y＝f（x）在区间［x，x＋Δx］上的最大值和最小值），于是

令Δx→0，由于函数f（x）在x处连续，则

即Φ（x）在［a，b］上可导并且Φ′（x）＝f（x）.

由定理1可知，变上限积分函数是其被积函数的一个原函数，因此连续函数的原函数必定存在.由此得到下面的原函数存在定理.

定理2（原函数存在定理）　设函数f（x）在区间［a，b］上连续，则函数Φ（x）＝就是f（x）在［a，b］上的一个原函数.