性质1设函数f（x）的原函数存在，k为非零常数，则证因为，所以类似可证明不定积分有下列性质.性质2设函数f（x）与g（x）的原函数均存在，则性质2可推广到有限个函数的情形.利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.对于不定积分运算需要指出，虽然每个积分号都含有任意常数，但任意常数之和仍是任意常数，所以遇到几个任意常数时只要写一个任意常数即可.例5求解例6求解积分运......
2023-11-19
高等数学上册：定积分性质解析
【摘要】：，n）.又由于Δxi≥0（i＝1，2，…，n），因此记λ＝max｛Δx1，Δx2，…
假设定积分
都是存在的，则有以下性质.
性质1 
证 由定积分的定义可得：
性质2 
证
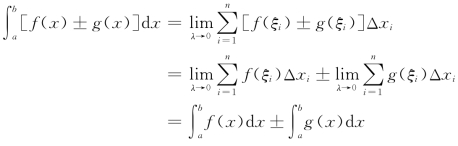
性质1对有限多个函数的代数和的积分也成立，类似证明即可.
性质3 
（k为常数）.
性质4（对区间的可加性） 对于任意三个数a，b，c，恒有
证 先证a＜c＜b的情形.因为函数f（x）在［a，b］上可积，所以无论对［a，b］怎样划分，和式的极限总是不变的.因此在划分区间时，可以使c是其中一个分点，那么在［a，b］上的积分和等于在［a，c］上的积分和加上在［c，b］上的积分和，即
令λ→0，对上式两端取极限得
当c＜a＜b时，由上面所证可知
所以
同理可证当a＜b＜c时，结论也成立.
综上结论成立.
性质4可以推广到一般情形.如对于任意四个数a，b，c，d，恒有
性质5 如果在区间［a，b］上f（x）≥0，则
证 因为f（x）≥0，所以f（ξi）≥0（i＝1，2，…，n）.
又由于Δxi≥0（i＝1，2，…，n），因此
记λ＝max｛Δx1，Δx2，…，Δxn｝，则
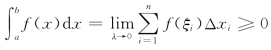
推论1 如果在区间［a，b］上f（x）≤g（x），则
推论2 
注 推论1与推论2的证明由性质5易得，请读者自行完成.
性质6（估值定理） 设M，m是函数f（x）在区间［a，b］上的最大值与最小值，则
证 因为m≤f（x）≤M，由性质5的推论1，得
所以
性质7（积分中值定理） 设函数f（x）在区间［a，b］上连续，则在［a，b］上至少存在一点ξ，使得(www.chuimin.cn)
成立.
证 因为f（x）在［a，b］上连续，所以f（x）在［a，b］上有最小值m和最大值M，由性质6得
即
是介于f（x）的最小值与最大值之间的一个数，根据闭区间上连续函数的介值定理，至少存在一点ξ∈［a，b］，使得
即
积分中值定理有以下几何解释：设f（x）为闭区间［a，b］上的连续函数，则以区间［a，b］为底边、曲线y＝f（x）为曲边的曲边梯形的面积等于相同底边、高为f（ξ）的一个矩形的面积（图5－4）.
图5－4
称
为函数f（x）在区间［a，b］上的平均值.
定积分的性质对于定积分的计算及进一步研究定积分的理论都有重要作用.
例3 比较下列各对积分值的大小：
解 （1）因为x∈［0，1］时，ex≥x2，所以由性质5的推论1得
（2）因为
时，sinx≥cosx，所以由性质5的推论1得
因此
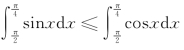
例4 设f（x）在区间［0，1］上连续，在（0，1）内可导，且
证明：在（0，1）内有一点c使f′（c）＝0.
分析 由条件和结论容易想到应用罗尔定理，只需再找出条件f（ξ）＝f（0）即可.
证 因为f（x）在［0，1］上连续，由积分中值定理可得，至少存在一点ξ∈
使得
于是由罗尔定理可得，至少存在一点c∈（0，ξ）⊂（0，1），使f′（c）＝0.
例5 求从0到T这段时间内自由落体运动的平均速度.
解 因为自由落体运动的速度v＝gt，所以
利用定积分定义，反过来可以求某些特殊数列的极限.
例6 求
解 由于
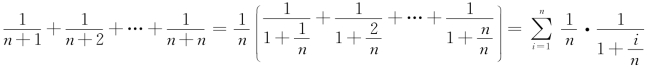
这可理解为将区间［1，2］等分为n个子区间，其长度为
n），取ξi为子区间的右端点
故
原式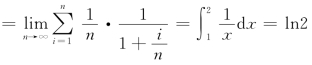
（定积分的计算下节将介绍）
上例也可化为定积分
请读者自行考虑.
有关高等数学 上册的文章
- 详细阅读
-
定积分的几何意义-高等数学 上册详细阅读
若函数f（x）≥0，则在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形的面积.当函数f（x）≤0时，由定积分定义知在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形（在x轴下方）的面积的相反数.图5－3一般地，若f（x）在［a，b］上既取得正值又取得负值，则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5－3所示，有由几何意义易知，在......
2023-11-19
-
高等数学上册：定积分换元法详细阅读
定理1设函数f（x）在［a，b］上连续，函数x＝φ（t）满足条件：（1）φ（α）＝a，φ（β）＝b，且a≤φ（t）≤b.（2）φ（t）在［α，β］（或［β，α］）上有连续导数.则有公式（5－5）称为定积分的换元公式.证由于f（x）在［a，b］上连续，则存在原函数，在［a，b］上可积.设F′（x）＝f（x），则又｛F［φ（t）］｝′＝F′［φ（t）］·φ′（t）＝f［φ（t）］·φ′（t），于是......
2023-11-19
-
如何求不定积分-高等数学上册详细阅读
定义2若F（x）是f（x）在区间I上的一个原函数，则称F（x）＋C为f（x）在区间I上的不定积分，记作即∫f（x）dx＝F（x）＋C其中C为任意常数，记号“∫”称为积分号，f（x）称为被积函数，f（x）dx称为被积表达式，x称为积分变量.由定义2可知，求的关键就是求出f（x）的一个原函数，不定积分与原函数是总体与个体的关系.由此，本节开头所举的两个例子可写作从不定积分的定义即可知下述关系：或又由......
2023-11-19
-
高等数学上册：极限性质详细阅读
利用函数极限的定义，可得下列极限的性质.1）唯一性定理2若存在，则极限唯一.证（反证法）假设极限不唯一，则存在两个不相等的常数a，b，使得均成立.不妨设b＞a，由于取则δ1＞0，当x满足0＜｜x－x0｜＜δ1时，恒有即又由于仍取则δ2＞0，当x满足0＜｜x－x0｜＜δ2时，恒有即取δ＝min｛δ1，δ2｝，则当x满足0＜｜x－x0｜＜δ时，上面（1－5）、（1－6）两式均成立，但这是不可能的.......
2023-11-19
-
高等数学：不定积分概念与性质详细阅读
一、原函数与不定积分定义4.1 设f（x）是定义在区间I上的函数，如果存在函数F（x），对于任意x∈I，都有F′（x）=f（x）或dF（x）=f（x）dx则称函数F（x）为函数f（x）在区间I上的一个原函数.例如，因为（sinx）′=cosx，则sinx是cosx的原函数.又因为（sinx+1）′=cosx，所以sinx+1也是cosx的原函数.由此例可以看出，一个函数若有原函数，则原函数可以不止......
2023-11-22
-
高等数学：定积分的概念和性质详细阅读
一、引例1.曲边梯形的面积设函数y=f（x）在闭区间[a，b]上非负且连续，则曲线y=f（x）与直线x=a，x=b，y=0围成的图形（见图5-1）称为曲边梯形.求其面积A的基本思想是在很小的区间上用小矩形面积近似代替小梯形面积.图5-1第一步：分割.用一串分点a=x0＜x1＜…......
2023-11-22
-
高等数学上册：定积分的元素法详细阅读
为总结出定积分应用的一般思想和方法，我们先回顾一下用定积分求曲边梯形面积问题的方法和步骤.设f在区间［a，b］上连续，且f≥0，求以曲线y＝f为曲边的［a，b］上的曲边梯形的面积A.把这个面积A表示为定积分的思路是“分割、取近似、求和、取极限”，具体步骤是：图6－1分割：将［a，b］分成n个小区间，相应地把曲边梯形分成n个小曲边梯形，其面积记作ΔAi（i＝1，2，…......
2023-11-19
相关推荐