首页理论教育定积分的几何意义-高等数学上册

定积分的几何意义-高等数学上册

2023-11-19 理论教育版权反馈

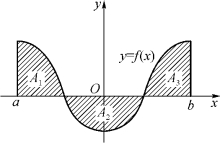
【摘要】：若函数f（x）≥0，则在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形的面积.当函数f（x）≤0时，由定积分定义知在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形（在x轴下方）的面积的相反数.图5－3一般地，若f（x）在［a，b］上既取得正值又取得负值，则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5－3所示，有由几何意义易知，在

若函数f（x）≥0，则在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形的面积.

当函数f（x）≤0时，由定积分定义知在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形（在x轴下方）的面积的相反数.

pagenumber_ebook=196,pagenumber_book=185

图5－3

一般地，若f（x）在［a，b］上既取得正值又取得负值，则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5－3所示，有

由几何意义易知，在［a，b］上，若f（x）＝1，则

因此，引例中的曲边梯形的面积变力F（x）在［a，b］上所做的功

函数f（x）在［a，b］上满足什么条件一定可积呢？对于这个问题我们不作深入讨论，仅给出以下两个充分条件.

定理1　若f（x）在区间［a，b］上连续，则f（x）在［a，b］上可积.

定理2　若f（x）在区间［a，b］上有界，且仅有有限个第一类间断点，则f（x）在［a，b］上可积.

例1　利用定积分定义计算

解　因为函数f（x）＝x在积分区间［0，1］上连续，所以定积分存在.又因为定积分与区间［0，1］的分割方式及点ξi的取法无关，因此，为方便计算，可对［0，1］作特殊分法，对点ξi作特殊取法.(www.chuimin.cn)

（1）将区间［0，1］分成n等份，分点为每个小区间［xi－1，xi］的长度

（2）取每个小区间的右端点为ξi，即作乘积

（3）求和，得

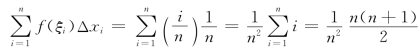
pagenumber_ebook=197,pagenumber_book=186

（4）取极限：当λ→0，即n→∞时，由定积分的定义得

例2　利用定积分的几何意义计算下面的积分：.

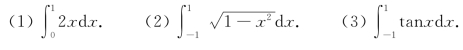
pagenumber_ebook=197,pagenumber_book=186

解　（1）由定积分的几何意义可知为x轴、x＝1及y＝2x所围直角三角形面积，故

（2）由定积分的几何意义可知等于上半圆周x2＋y2＝1（y≥0）与x轴所围成的图形的面积，故

（3）由定积分的几何意义可知等于x轴、y＝tanx、x＝1及x＝－1四条线所围成的平面图形面积的代数和.由y＝tanx的对称性可知

从上面的例子不难看出，定积分的计算如果仅仅依赖定义和几何意义，那将受到很大的局限，只有一些特殊的定积分能较快地计算出来.因此有必要进一步讨论定积分的计算方法，为此下面我们首先给出定积分的基本性质.