表示常量,用字母x,y,z,t,…......
2023-11-19
有些不定积分![]() 难以用凑微分的方法来积分,比如
难以用凑微分的方法来积分,比如![]()
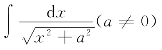 等.但此时若作适当的x=φ(t)变 换 后
等.但此时若作适当的x=φ(t)变 换 后![]()
![]() 会变得容易积分,这种换元积分的方法称为第二类换元积分法,具体叙述如下.
会变得容易积分,这种换元积分的方法称为第二类换元积分法,具体叙述如下.
定理2 设x=φ(t)有连续的导函数,且φ′(t)≠0,又设![]() F(t)+C,则有
F(t)+C,则有
![]()
其中φ-1(x)是x=φ(t)的反函数.
证 只需证明两个不定积分有相同的原函数即可.
因为F(t)是f(φ(t))φ′(t)的原函数,记Φ(x)=F(φ-1(x)),则
![]()
即Φ(x)为f(x)的原函数,于是定理得证.
利用第二类换元法解题的一般步骤为:
![]()
第一类和第二类换元积分法都是依据同一个公式![]()
![]() 它们的基本思想是一致的,都是通过变量代换把较复杂的不定积分化成容易解决的不定积分,两者仅仅是方向不同.
它们的基本思想是一致的,都是通过变量代换把较复杂的不定积分化成容易解决的不定积分,两者仅仅是方向不同.
常用的第二类换元法有三角代换、根式代换与倒代换,下面通过例题依次介绍.
1)三角代换
例17 求![]()
解 令![]() 则
则
![]()
于是
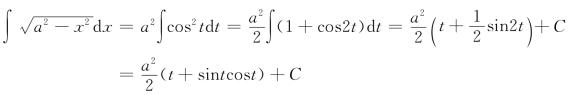
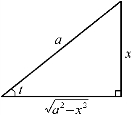
图4-2
为了把最后一式还原为x的表达式,可以将t看成锐角,根据![]() 作辅助直角三角形(图4-2)得到
作辅助直角三角形(图4-2)得到
![]()
因此
![]()
例18 求![]()
解 令![]() 则
则
![]()
于是
![]()
根据![]() 作辅助直角三角形(图4-3),有
作辅助直角三角形(图4-3),有
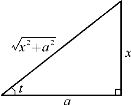
图4-3
![]()
因此
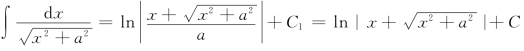
其中C=C1-lna.
例19 求![]() (www.chuimin.cn)
(www.chuimin.cn)
解 被积函数的定义域为(-∞,-a)∪(a,+∞).
当x∈(a,+∞)时,令![]() asecttantdt,于是
asecttantdt,于是
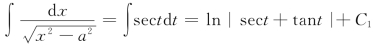
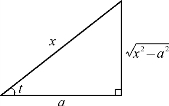
图4-4
根据![]() 作辅助直角三角形(图4-4),有tant=
作辅助直角三角形(图4-4),有tant=![]() ,因此
,因此
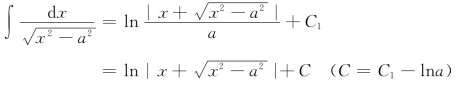
当x∈(-∞,-a)时,令x=-u,于是u>a>0,且有
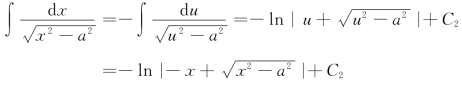

故当|x|>a时,总有![]()
从以上三例可以看出,被积函数中含有![]() 时,常常可分别令
时,常常可分别令![]()
![]() 等代换化去根式,将无理函数转化为三角函数的积分,以上所用的代换统称为三角代换.
等代换化去根式,将无理函数转化为三角函数的积分,以上所用的代换统称为三角代换.
2)根式代换
例20 求![]()
解 令![]() 则x=t2,dx=2tdt,于是
则x=t2,dx=2tdt,于是

例21 求![]()
解 令![]() 于是
于是
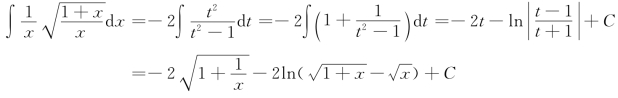
对形如![]() 为常数)型函数的积分,可作变量代换
为常数)型函数的积分,可作变量代换![]() t,把无理函数转化为有理函数R(x,t)的积分,其中R(x,t)表示x和t两个变量的有理式.
t,把无理函数转化为有理函数R(x,t)的积分,其中R(x,t)表示x和t两个变量的有理式.
对形如![]() (a,b,c,d为常数)型函数的积分,可作变量代换
(a,b,c,d为常数)型函数的积分,可作变量代换![]() ,转化为函数R(x,t)的积分,其中R(x,t)仍表示x和t两个变量的有理式.
,转化为函数R(x,t)的积分,其中R(x,t)仍表示x和t两个变量的有理式.
例22 求![]()
解 令![]() 于是
于是
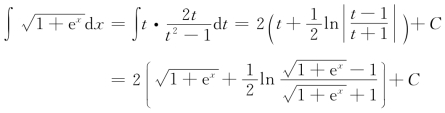
3)倒代换
例23 求![]()
解 当被积函数中分母的次数较高时,可以作代换![]() (倒代换),即令x=
(倒代换),即令x=![]() 则
则![]() 于是
于是
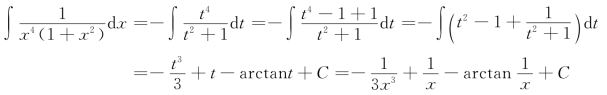
在本节的例题中,有几个积分经常用到.它们通常也被当作公式使用.因此,除了前面介绍的基本积分公式外,再补充下面几个基本积分公式(其中常数a>0).

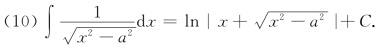
例24 求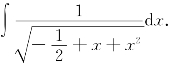
解

变量代换是数学中常用的思想和方法,换元积分法的关键也同样是作变量代换.变量代换的实质是对应,通过对应将不便计算的不定积分类型转化为便于计算的积分类型.
有关高等数学 上册的文章

要比较准确地描绘出一般函数的图形,仅用描点作图是不够的,为了提高作图的准确性,可将前面讨论的函数性态应用到曲线的作图上,即先利用函数的一阶、二阶导数,分析函数的单调性、极值、凹凸性与拐点等整体性态,并求出曲线的渐近线,然后再描点作图,称这种作图的方法为分析作图法.其一般步骤如下:(1)确定f(x)的定义域、间断点,并讨论函数的奇偶性、周期性.(2)在定义区间内求函数f(x)的一阶、二阶导数为零或不......
2023-11-19

平面曲线的长度称为弧长.由于曲线的弧长具有可加性,下面用元素法来讨论平面曲线弧长的计算公式.设曲线弧由直角坐标方程y=f(x)(a≤x≤b)给出,其中f(x)在[a,b]上具有一阶连续导数,求曲线L的弧长s.如右图6-20所示,取x为积分变量,则积分区间为[a,b],任取区间[x,x+dx][a,b],由弧微分公式可知弧长元素为图6-20故曲线弧长为若平面曲线L由参数方程给出,x=φ(x),y=ψ......
2023-11-19

解设圆柱形密闭锅炉的底半径为R,高为h,则其表面积S=2πRh+2πR2由将它代入上式得由解得唯一的驻点又由于制造固定容积的圆柱形密闭锅炉时,一定存在一个底半径,使锅炉的表面积最小.因此,当时,S在该点取得最小值.此时,相应的高即当圆柱形密闭锅炉的高与底直径都等于时,表面积最小,从而使用料最省.......
2023-11-19

)时无意义,故x=kπ(k=0,±1,±2,…)均为的间断点.当x=0时,由于故x=0为f的第一类可去型间断点;当x=kπ(k=±1,±2,…)为f的第二类无穷型间断点.......
2023-11-19

1)反函数的求导法则求导法则Ⅱ设y=f(x)在区间Ix内单调、可导,且f′(x)≠0,则其函数x=φ(y)在相应的区间Iy内也单调、可导,且证设函数的y=f(x)的反函数x=φ(y)的自变量y的增量为Δy,则相应地x的增量为Δx.由函数可导必连续的性质及反函数的连续性可得,x=φ(y)在区间Iy内单调、连续,因此当Δy→0时,有Δx→0.且当Δy≠0时,有Δx≠0,则y,y+Δy∈Iy,设Δy......
2023-11-19
相关推荐