定义2若F（x）是f（x）在区间I上的一个原函数，则称F（x）＋C为f（x）在区间I上的不定积分，记作即∫f（x）dx＝F（x）＋C其中C为任意常数，记号“∫”称为积分号，f（x）称为被积函数，f（x）dx称为被积表达式，x称为积分变量.由定义2可知，求的关键就是求出f（x）的一个原函数，不定积分与原函数是总体与个体的关系.由此，本节开头所举的两个例子可写作从不定积分的定义即可知下述关系：或又由......
2023-11-19
高等数学上册：不定积分性质总结
【摘要】：性质1设函数f（x）的原函数存在，k为非零常数，则证因为，所以类似可证明不定积分有下列性质.性质2设函数f（x）与g（x）的原函数均存在，则性质2可推广到有限个函数的情形.利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.对于不定积分运算需要指出，虽然每个积分号都含有任意常数，但任意常数之和仍是任意常数，所以遇到几个任意常数时只要写一个任意常数即可.例5求解例6求解积分运
性质1 设函数f（x）的原函数存在，k为非零常数，则
证 因为
，所以
类似可证明不定积分有下列性质.
性质2 设函数f（x）与g（x）的原函数均存在，则
性质2可推广到有限个函数的情形.
利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.
对于不定积分运算需要指出，虽然每个积分号都含有任意常数，但任意常数之和仍是任意常数，所以遇到几个任意常数时只要写一个任意常数即可.
例5 求
解
例6 求
解 
积分运算中会对某些分式函数的分子进行“插项”，这种通过“插项”进而分项的方法经常被应用.
例7 求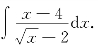
(www.chuimin.cn)
解
例8 求
解 用三角恒等式tan2x＝sec2x－1把被积函数统一化为sec2x的函数，再积分，即
例9 求
解 
例10 求
解 分子分母都是三次多项式函数，被积函数为假分式，需先分解为多项式与真分式的和，再逐项积分，即
例11 若f（x）的一个原函数是2x，求
解 因为2x是f（x）的原函数，故f（x）＝（2x）′＝2xln2，所以
需要指出的是，在计算不定积分时有时会得到实质一致而形式不同的结果，例如
都是正确的.
要验证不定积分结果正确与否，只要验证等式右端的导数是否等于被积函数.这是我们证明不定积分恒等式、验证不定积分计算正确与否的常用方法.
有关高等数学 上册的文章
- 详细阅读
-
高等数学上册：极限性质详细阅读
利用函数极限的定义，可得下列极限的性质.1）唯一性定理2若存在，则极限唯一.证（反证法）假设极限不唯一，则存在两个不相等的常数a，b，使得均成立.不妨设b＞a，由于取则δ1＞0，当x满足0＜｜x－x0｜＜δ1时，恒有即又由于仍取则δ2＞0，当x满足0＜｜x－x0｜＜δ2时，恒有即取δ＝min｛δ1，δ2｝，则当x满足0＜｜x－x0｜＜δ时，上面（1－5）、（1－6）两式均成立，但这是不可能的.......
2023-11-19
- 详细阅读
-
高等数学：不定积分概念与性质详细阅读
一、原函数与不定积分定义4.1 设f（x）是定义在区间I上的函数，如果存在函数F（x），对于任意x∈I，都有F′（x）=f（x）或dF（x）=f（x）dx则称函数F（x）为函数f（x）在区间I上的一个原函数.例如，因为（sinx）′=cosx，则sinx是cosx的原函数.又因为（sinx+1）′=cosx，所以sinx+1也是cosx的原函数.由此例可以看出，一个函数若有原函数，则原函数可以不止......
2023-11-22
-
高等数学上册：无穷大量的定义及性质详细阅读
在前面，已经多次提到“无穷大”这个概念，这里对这一变化状态给出确切的定义.我们知道，当x→□时，对应函数的绝对值｜f（x）｜无限增大，就称函数f（x）为当x→□时的无穷大量.设M为任意取定的大正数M，则不等式｜f（x）｜＞M表示函数的绝对值｜f（x）｜可以超过预先任意给定的大正数M，因此由M的任意性可知，不等式｜f（x）｜＞M表示函数的绝对值无限增大.再结合无穷大对应的极限过程的精确描述，由此得到......
2023-11-19
-
高等数学上册：不定积分的分部积分法详细阅读
上节我们在复合函数求导法则的基础上，给出了转化不定积分的重要方法——换元积分法.但有很多积分如等利用换元积分仍然无法积出.本节将在函数乘积的求导公式的基础上，推导出转化不定积分的另一重要方法——分部积分法.设函数u＝u（x），v＝v（x）具有连续的导数，那么两个函数乘积的求导公式为（uv）′＝u′v＋uv′移项得uv′＝（uv）′－u′v对上式两边积分得或公式（4－2）或（4－3）称为不定积分的分......
2023-11-19
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2023-11-19
-
数列极限：高等数学上册详细阅读
对于给定的数列｛xn｝，我们讨论当项数n无限增大时（记作n→∞），对应项的变化趋势.观察上面的四个数列，容易看出，当n→∞时，数列趋于1；数列各项的值在数1的两侧来回交替着变化，且越来越接近1；数列｛2n－1｝越来越大，无限增大；数列｛1－（－1）n｝各项的值永远在0与2之间交互取得，而不与某一数接近.如果当n→∞时，数列的项xn能无限接近于某个常数A，则称这个数列为收敛数列，常数A称为当n→∞时......
2023-11-19
相关推荐