重载型自动扶梯出于对安全性的要求，曲率半径一般都比较大。重载型自动扶梯常用的曲率半径如表11-2-2所示。......
2025-09-29
高等数学上册：曲率与曲率半径解析
【摘要】：下面研究曲线各部分的弯曲程度.观察下面的两张图（图3－16（a）和（b））.图3－16在图3－16（a）中，曲线L与L1为平面上两条连续光滑的曲线，在L与L1上分别取长度都等于Δs的弧段在曲线L上动点沿弧从点P移动到点Q时，其切线也连续转动，设其倾斜角的改变量（即弧段两端切线的夹角）为Δα，同样设曲线L1上动点沿弧从点P移动到点Q1时，其切线的倾角的改变量（即弧段两端切线的夹角）为Δα1，从图3－
下面研究曲线各部分的弯曲程度.观察下面的两张图（图3－16（a）和（b））.
图3－16
在图3－16（a）中，曲线L与L1为平面上两条连续光滑的曲线，在L与L1上分别取长度都等于Δs的弧段
在曲线L上动点沿弧
从点P移动到点Q时，其切线也连续转动，设其倾斜角的改变量（即弧段
两端切线的夹角）为Δα，同样设曲线L1上动点沿弧
从点P移动到点Q1时，其切线的倾角的改变量（即弧段
两端切线的夹角）为Δα1，从图3－16（a）可看出，弧段
的长度
的长度，但Δα＜Δα1，而显然弧
的弯曲程度比
的弯曲程度小，这说明曲线的弯曲程度与其切线的倾角的改变量Δα成正比.
从图3－16（b）上可看出，当L与L1上的动点处的切线转过同样的角度Δα时，弧长较短的
的弯曲程度比弧长较长的
的弯曲程度大，这说明曲线的弯曲程度与弧段的长度Δs成反比.
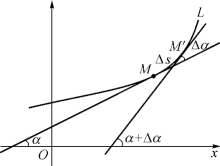
图3－17
在光滑的曲线L上取点M与M′（图3－17），过M与M′分别作曲线的切线，设切线转过的角度为Δα，弧长
表示弧段
的平均弯曲程度，称为弧段
的平均曲率，记作
下面给出曲线L在点M处的曲率的定义.
定义1 设M，M′为光滑曲线L上的两点
，从点M沿曲线L到M′时其切线转过的角度为Δα，当Δs→0时，如果弧段
的平均曲率的极限存在，则称此极限为曲线L在点M处的曲率，记作K，即
当导数
存在时，则
对于直线来说，由于其切线与该直线本身重合，切线的倾角α不变，即Δα＝0，从而直线上任意点处的曲率都等于零，这与“直线是不弯曲的”这一事实相一致.
例3 求半径为R的圆的曲率.
解 设M为该圆周上的任意一点，M′为圆周上与M邻近的点，圆弧
对应的中心角记作Δα，则
从而
.由曲率的定义
故圆上任一点处的曲率都等于其半径的倒数.这也就是说圆上每一点的弯曲程度都一样.这与圆给我们的直观感觉相一致.
下面根据曲率的定义来推导一般曲线上点的曲率的计算公式.
设曲线的直角坐标方程是y＝f（x），函数f（x）具有二阶导数.由于曲线y＝f（x）在点M处的切线的斜率为
y′＝tanα
对上式求x的导数，得
解得
又弧微分
于是有
从而得曲率的计算公式为
如果曲线C由参数方程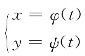
给出，则可由参数式函数的求导法，求出
将它们代入式（3－27），得曲线的曲率：
例4 求双曲线xy＝4在点M（2，2）处的曲率.
解 由xy＝4，得
则
在点M（2，2）处，y′＝－1，y″＝1.
代入曲率公式（3－27），得(https://www.chuimin.cn)
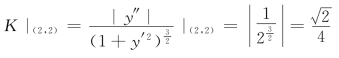
例5 计算椭圆x＝acost，y＝bsint在
处的曲率.
解 因为
x′＝－asint，x″＝－acost，y′＝bcost，y″＝－bsint
代入曲率的计算公式（3－28），得
将
代入上式，得
当曲线上某点处的曲率为K时，常常可以借助半径为
的圆形象地表示曲线在该点的弯曲程度.
定义2 曲线上某点M处的曲率K的倒数
称为曲线在点M处的曲率半径，记作R，即
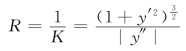
定义3 设曲线y＝f（x）在点M（x，y）处的曲率为K.在点M处的曲线的法线上，在凹的一侧取一点M0（x0，y0），使
.以R为半径，M0（x0，y0）为圆心作一个圆，则称此圆为曲线y＝f（x）在点M（x，y）处的曲率圆，M0（x0，y0）称为曲线在点M（x，y）处的曲率中心（图3－18）.
图3－18
由上述定义可知，如果设曲线y＝f（x）在M0（x0，y0）处的曲率圆方程为
（x－α）2＋（y－β）2＝R2
则可求得该曲率圆的圆心为
例6 求曲线xy＝4在点M（2，2）处的曲率圆.
解 由例4求得，在M（2，2）处
又由式（3－29）求得
故所求的曲率圆方程为
（x－4）2＋（y－4）2＝8
显然曲线与曲率圆有密切的关系：曲线与曲率圆在M0处有公共的切线、相同的曲率、相同的凹凸性.故曲率圆在切点处与曲线极为接近，所以曲率圆也叫密切圆.
在实际问题中，常用曲率圆在点M邻近的一段圆弧近似替代该点邻近的曲线弧使问题简单化.
例7 设有一金属工件的内表面截线为曲线
要将其内侧表面打磨光滑，问应该选用多大直径的砂轮效率最高？
解 在打磨时，如果砂轮直径过大，将会使加工点附近部分磨得过多，如果砂轮直径过小，则显然会增加打磨时间.故最合适的选择是：选曲率半径最小值对应的半径为砂轮的半径.
由于y′＝x，y″＝1，故曲线上任一点处的曲率为
曲率半径为
故当x＝0时，该曲线的曲率半径取最小值，Rmin＝1（长度单位）.因此选用的砂轮直径最大不能超过2Rmin＝2（长度单位），此时效率最高.
图3－19
例8 在修建铁路时，需要把铁轨由直线段转向半径为R的圆弧路段，为了避免离心率的突变，确保快速行进中的列车在转弯处平稳运行，要求轨道曲线有连续变化的曲率.因此需要在直线路段到圆弧路段之间衔接一段叫作缓和曲线的弯道
（见图3－19），以便铁轨的曲率从零连续地递增到
.讨论缓和曲线的方程.
解 在原点处的曲率为零的最简多项式为三次曲线，且其曲率从零连续地递增，因此在工程设计中通常采用三次抛物线作为铁路或公路的缓和曲线.
图3－19中
为直轨
为圆弧路轨，而
为缓和曲线，根据实际经验其方程选用
为待定系数）.
下面选定a使曲线
从原点O到点A这一段曲线弧的曲率从0增大到
记点A的横坐标为
故由曲率公式得
现实中R要比l大很多，于是
所以可取
从而所求的缓和曲线方程为
相关文章
- 详细阅读
-
炸药类型及活性球缺罩曲率半径详细阅读
在活性杆式射流形貌方面，活性球缺罩壁厚主要影响活性杆式射流的直径和长径比，随着活性球缺罩壁厚增加，活性杆式射流直径变大，但长度变化较小，导致活性杆式射流长径比减小。图2.66药型罩壁厚对活性杆式射流粒子分布的影响图2.6......
2025-09-29
-
外罩开槽式双层药型罩成型受曲率半径影响详细阅读
吴浩宇1，周春桂1，董方栋2，汤雪志1，王志军1摘要：在传统的双层药型罩形成串联EFP 的基础上，提出一种外罩开槽式的新型双层药型罩结构。利用ANSYS／LS-DYNA 软件对该结构的成型进行了数值模拟与分析，并分析了曲率半径对其形成毁伤元的影响。......
2025-09-29
-
ISDX曲线曲率图优化详细阅读
如图8.3.1所示，曲率图是显示曲线上每个几何点处的曲率或半径的图形，从曲率图上可以看出曲线变化方向和曲线的光滑程度，它是查看曲线质量最好的工具。在ISDX环境下，单击曲线的“显示曲率”按钮，然后选取要查看其曲率的曲线，即可显示曲线曲率图。图8.3.1 显示曲线曲率图图8.3.2 “曲率”对话框●在造型设计时，每当创建完一条ISDX曲线，最好都要用曲率图查看曲线的质量，不要单凭曲线的视觉表现。......
2025-09-29
-
高等数学：夹逼准则-高等数学 上册详细阅读
准则Ⅰ若函数f（x），g（x），h（x）在点x0的某去心邻域内满足条件：（1）g（x）≤f（x）≤h（x），（2）则存在，且等于a.证由于，因此，对ε＞0，δ1＞0，当x满足0＜｜x－x0｜＜δ1时，有｜g（x）－a｜＜ε，即又由于则对上面的ε＞0，δ2＞0，当x满足0＜｜x－x0｜＜δ2时，有｜h（x）－a｜＜ε，即取δ＝min｛δ1，δ2｝，则当x满足0＜｜x－x0｜＜δ时，（1－25）、......
2025-09-30
-
高等数学上册：导数概念详细阅读
1）几个实际问题（1）平面曲线的切线问题设点M0（x0，y0）与M（x，y）分别是平面曲线y＝f（x）上的一个定点与动点，则割线MM0的斜率为根据切线的定义可知，当M→M0，即Δx→0时，若存在，则该极限就等于切线的斜率，即因此曲线y＝f（x）在点M0（x0，y0）处的切线方程为y－y0＝k（x－x0）（2）变速直线运动的瞬时速度问题设质点M沿某直线作s＝s（t）的变速直线运动，s（t）为t时刻质......
2025-09-30
-
城市桥梁抗震验算结果及等效屈服曲率详细阅读
在E1和E2地震作用下，各类城市桥梁的抗震验算目标应满足表7.8-2的要求。采用非线性时程进行地震反应分析的桥梁可按式验算转角。图7.8-4 等效屈服曲率......
2025-09-30
-
UGNX10.0曲线曲率分析技巧详细阅读
本节将简单介绍曲线特性分析的一般方法及操作过程。说明除非特意关闭，否则曲线的分析结果会一直显示在图形上，关闭时需要选中该曲线，再次选择下拉菜单命令即可。图6.1.48 曲率梳图“峰值”分析。选取图6.1.49a所示的曲线。图6.1.50 拐点分析图表显示结果。选择下拉菜单命令，系统打开一个“图表”电子表格显示分析结果，图6.1.51所示为图表分析结果。......
2025-09-30
相关推荐