平面曲线的长度称为弧长.由于曲线的弧长具有可加性，下面用元素法来讨论平面曲线弧长的计算公式.设曲线弧由直角坐标方程y＝f（x）（a≤x≤b）给出，其中f（x）在［a，b］上具有一阶连续导数，求曲线L的弧长s.如右图6－20所示，取x为积分变量，则积分区间为［a，b］，任取区间［x，x＋dx］［a，b］，由弧微分公式可知弧长元素为图6－20故曲线弧长为若平面曲线L由参数方程给出，x＝φ（x），y＝ψ......
2023-11-19
高等数学上册：光滑曲线弧的长度计算
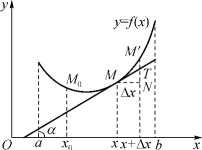
【摘要】：图3－15如果函数y＝f（x）在区间（a，b）内有连续的导数，这时切线沿曲线是连续变化的，称这种曲线y＝f（x）是（a，b）内的光滑曲线.理论上可以证明：光滑曲线弧是可以求长度的.在（a，b）内光滑曲线y＝f（x）上取定一点M0（x0，y0）作为度量曲线弧长的基点（图3－15），并规定沿x增大的方向为曲线的正方向（弧长增加的方向），对曲线上任意的点M（x，y），规定有向弧段的值s（x）（也称弧函数
图3－15
如果函数y＝f（x）在区间（a，b）内有连续的导数，这时切线沿曲线是连续变化的，称这种曲线y＝f（x）是（a，b）内的光滑曲线.理论上可以证明：光滑曲线弧是可以求长度的.
在（a，b）内光滑曲线y＝f（x）上取定一点M0（x0，y0）作为度量曲线弧长的基点（图3－15），并规定沿x增大的方向为曲线的正方向（弧长增加的方向），对曲线上任意的点M（x，y），规定有向弧段
的值s（x）（也称弧函数s（x））如下：s（x）的绝对值等于弧
的长度，当有向弧段
的方向与曲线的正向一致时s（x）＞0，相反时s（x）＜0.由此得到一个定义在区间（a，b）内的弧函数s（x），若也用
表示弧
的长度，则
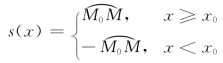
显然s（x）是x的单调增加函数.下面给出弧函数s（x）的导数及微分公式.
设点x与x＋Δx在区间（a，b）内，它们对应曲线y＝f（x）上相应的两点M（x，f（x））与M′（x＋Δx，f（x＋Δx）），则函数y＝f（x）相应的增量是Δy，弧函数s（x）相应的增量
由于s（x）是x的单调增加函数，因此
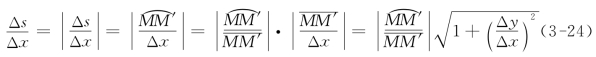
令Δx→0，则M′→M.由于
因此对式（3－24）求Δx→0时的极限，可得
则
式（3－25）称为曲线y＝f（x）的弧微分公式.由式（3－25）可得
（ds）2＝（dx）2＋（dy）2 （3－26）
式（3－26）中的三个微分的绝对值构成了图3－16中的直角三角形MNT的三条边，因此称MNT为微分三角形.弧微分是微分三角形的有向斜边（在切线MT上而不是在弦MM′上）的值.若设切线MT的倾斜角为
由微分三角形MNT可得
(www.chuimin.cn)
当α为负角时，以上两个等式也成立.
由式（3－25）可推得常用曲线方程对应的弧微分公式：
（1）若光滑曲线的方程为y＝f（x），则
.
（2）若光滑曲线的方程为x＝g（y），则
（3）若光滑曲线的参数方程为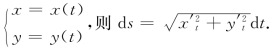
（4）若光滑曲线的极坐标方程为ρ＝ρ（θ），则
例1 求曲线y＝x3的弧微分.
解 因为y′＝3x2，所以
例2 求旋轮线x＝a（t－sint），y＝a（1－cost）（a＞0）的弧微分.
解 因为
所以
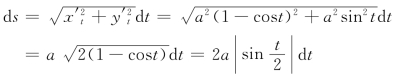
有关高等数学 上册的文章
- 详细阅读
-
高等数学上册：曲线凹凸性与拐点详细阅读
并求此时曲线的凹凸区间.解y″＝12ax2＋6bx由于点（1，3）在该曲线上，将点（1，3）代入该曲线方程中得a＋b＝3又点（1，3）为曲线的拐点，故解得a＝－3，b＝6.此时y″＝－36x2＋36x＝36，由y″＝36＝0，解得x1＝0，x2＝1.列表表示如下.表3－3由表3－3可知，曲线的凸区间为，曲线的凹区间为［0，1］.利用凹凸性可以证明一类特殊的不等式.例8证明证取所以在上，曲线f＝tant是凹的.因此当时，有即......
2023-11-19
-
定积分的几何意义-高等数学 上册详细阅读
若函数f（x）≥0，则在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形的面积.当函数f（x）≤0时，由定积分定义知在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形（在x轴下方）的面积的相反数.图5－3一般地，若f（x）在［a，b］上既取得正值又取得负值，则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5－3所示，有由几何意义易知，在......
2023-11-19
-
高等数学基础：曲线凹凸和拐点详细阅读
一、曲线凹凸性的定义为了较准确地描述函数的图形，仅知道函数的单调区间和极值是不行的，比如说，f（x）在[a，b]上单调，这时会出现图3.6中的几种情况，l1是一段凸弧，l2是一段凹弧，l3既有凸的部分，也有凹的部分，曲线具有这种凸和凹的性质，称为凸凹性.图3.6曲线的凸凹性从几何意义上看，凸弧具有这种特点：从中任取两点，连接此两点的弦总在曲线的下方.进而不难知道，在[a，b]中任意取两个点函数在......
2023-11-20
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2023-11-19
-
数列极限：高等数学上册详细阅读
对于给定的数列｛xn｝，我们讨论当项数n无限增大时（记作n→∞），对应项的变化趋势.观察上面的四个数列，容易看出，当n→∞时，数列趋于1；数列各项的值在数1的两侧来回交替着变化，且越来越接近1；数列｛2n－1｝越来越大，无限增大；数列｛1－（－1）n｝各项的值永远在0与2之间交互取得，而不与某一数接近.如果当n→∞时，数列的项xn能无限接近于某个常数A，则称这个数列为收敛数列，常数A称为当n→∞时......
2023-11-19
-
高等数学上册：函数极值详细阅读
定义1凡是满足方程f′（x）＝0的点x称为函数f（x）的驻点.根据导数的几何意义，在曲线y＝f（x）上驻点处的切线是水平的.图3－9在图3－9中，考察函数f（x）在［a，b］上的极值与最值，发现：函数f（x）在点x1，x2，x3处取得极大值，函数f（x）在x′1，x′2，x′3处取得极小值；其最大值为f（b），最小值为f（x′2）.观察该图还发现：函数在一个区间内可以有若干个极大值与极小值，函数......
2023-11-19
-
函数单调性-高等数学 上册详细阅读
函数的单调性是函数的主要性质之一，下面利用导数来研究函数的单调性的判别方法.从图3－4（a）中可看出，当沿着单调增加函数的曲线从左向右移动时，曲线逐渐上升，它的切线的倾斜角α总是锐角，即这时斜率f′（x）＞0；从图3－4（b）中可看出，当沿着单调减少函数的曲线从左向右移动时，曲线逐渐下降，其切线的倾斜角α总是钝角，即这时斜率f′（x）＜0.图3－4从上面的几何直观中可得出：当函数在区间内是单调增加......
2023-11-19
相关推荐