首页理论教育曲线渐近线的重要性及示例

曲线渐近线的重要性及示例

2023-11-19 理论教育版权反馈

【摘要】：定义若曲线y＝f（x）上的动点沿曲线运动到无穷远处时，此动点与某一定直线l的距离趋近于零，则称此直线l为该曲线y＝f（x）的一条渐近线.渐近线表示了曲线无限延伸的方向与趋势.一般地，渐近线可分铅直渐近线、水平渐近线和斜渐近线三类，下面依次讨论它们的求法.1）铅直渐近线如果当x→x0（或或时，f（x）→∞，即则直线x＝x0是曲线y＝f（x）的一条铅直渐近线（图3－12）.图3－12例如，对曲线＋∞

定义　若曲线y＝f（x）上的动点沿曲线运动到无穷远处时，此动点与某一定直线l的距离趋近于零，则称此直线l为该曲线y＝f（x）的一条渐近线.

渐近线表示了曲线无限延伸的方向与趋势.一般地，渐近线可分铅直渐近线、水平渐近线和斜渐近线三类，下面依次讨论它们的求法.

1）铅直渐近线

如果当x→x0（或或时，f（x）→∞，即

则直线x＝x0是曲线y＝f（x）的一条铅直渐近线（图3－12）.

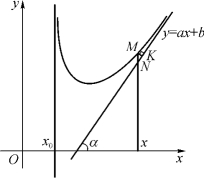
pagenumber_ebook=151,pagenumber_book=140

图3－12

例如，对曲线＋∞，所以直线x＝0为曲线的一条铅直渐近线.

又如曲线当x→－1时，y→∞，所以x＝－1为该曲线的一条铅直渐近线.

2）斜渐近线

设直线为曲线y＝f（x）的一条斜渐近线（图3－12）.曲线上的点M与直线y＝ax＋b的距离为｜MK｜，由渐近线的定义可知

在Rt△MKN中因此，由

MN＝f（x）－（ax＋b）

所以

由此，曲线y＝f（x）的斜渐近线的存在及求法问题归结为确定a，b的值，使它满足式（3－21）.为此将式（3－21）化为

从而

(www.chuimin.cn)

即

将式（3－22）代入式（3－21）中，得

从而可求得曲线y＝f（x）的斜渐近线为y＝ax＋b.

特别地，若a＝0，则这时y＝b为曲线y＝f（x）的一条水平渐近线.

综上所述，可得渐近线的求法如下：

（1）若则直线x＝x0是曲线y＝f（x）的一条铅直渐近线.

（2）若则直线y＝b是曲线y＝f（x）的一条水平渐近线.

（3）若则直线y＝ax＋b是曲线y＝f（x）的一条斜渐近线.

例1　求曲线的渐近线.

解　因为所以y＝2是该曲线的一条水平渐近线.

因为又函数y是偶函数，所以x＝±1是曲线的两条铅直渐近线.

例2　求曲线的渐近线.

解　因为所以直线x＝2为该曲线的一条铅直渐近线.因为

这时

所以该曲线的斜渐近线为y＝x＋2.