首页理论教育高数上册-函数最大最小值

高数上册-函数最大最小值

2025-09-30 理论教育版权反馈

【摘要】：解设圆柱形密闭锅炉的底半径为R，高为h，则其表面积S＝2πRh＋2πR2由将它代入上式得由解得唯一的驻点又由于制造固定容积的圆柱形密闭锅炉时，一定存在一个底半径，使锅炉的表面积最小.因此，当时，S在该点取得最小值.此时，相应的高即当圆柱形密闭锅炉的高与底直径都等于时，表面积最小，从而使用料最省.

1）连续函数在闭区间上的最大值与最小值

由连续函数的性质可知，闭区间上连续的函数必存在最大值与最小值.该最大值与最小值可能出现在区间的端点，也可能出现在区间的内部，若出现在区间的内部，则它必定是函数的极值.因此，要求函数在闭区间上的最大值与最小值，只要把区间内的所有极值以及端点处的函数值都求出来，则它们中的最大值与最小值，分别就是函数在闭区间上的最大值与最小值.因此求函数f（x）在闭区间［a，b］上的最大值与最小值的步骤为：

（1）求出导数的零点（即驻点）以及导数不存在的点.

（2）求出驻点与不可导点处对应的函数值，及端点处的函数值f（a），f（b）.

（3）将上述函数值进行比较，它们中的最大值与最小值分别就是函数f（x）在闭区间上的最大值与最小值.

例4　求在闭区间［0，4］上的最大值与最小值.

解　显然函数在闭区间［0，4］上连续，故它在［0，4］上

必有最大值与最小值，求导得

y′＝3x2＋3x－6＝3（x＋2）（x－1）

由y′＝0，得x1＝－2（不在讨论的区间内，舍去），x2＝1，算得

因此，在区间［0，4］上，函数在x＝4处取得最大值65，在x＝1处取得最小值

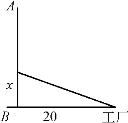
pagenumber_ebook=148,pagenumber_book=137

图3－10

例5　从北到南的一条高铁经过相距为200km的A、B两城，某工厂位于B城正东20km处，拟从高铁沿路上某点处修建高铁站，并从该高铁站修一条公路到工厂（图3－10）.若每吨货物的高铁运费为3元／km，公路运费为5元／km，问高铁站点应设在何处，可使从A城到工厂的运费最省？

解　设高铁站点取在铁路上距B城x km处，则每吨货物的运费

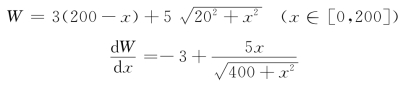pagenumber_ebook=148,pagenumber_book=137 (https://www.chuimin.cn)

由解得驻点x＝15.

又

W（15）＝680，W（0）＝700，W（200）＝1 005

因此，当x＝15时，W（x）取得最小值.即公路的起点应取在铁路线上离B城15km处，可使运费最省.

2）连续函数在开区间内的最大值与最小值

在开区间（a，b）内连续的函数不一定能在该区间内取得最大值与最小值.例如函数y＝x2在区间（－1，2）内的x＝0处取得最小值0，但无最大值；而在区间（1，2）内函数y＝x2既无最大值也无最小值.

特殊地，在实际问题中，如果函数在（a，b）内部只有一个驻点，而从实际意义分析中可判断出函数在（a，b）内有最大（或最小）值存在，则这个驻点就是所要求的最大（或最小）值点.

例6　制造容积为5πm3的圆柱形密闭锅炉，要使用料（表面积）最省，问锅炉的底半径与高应是多少？

解　设圆柱形密闭锅炉的底半径为R（m），高为h（m），则其表面积

S＝2πRh＋2πR2　（R∈（0，＋∞））

由将它代入上式得

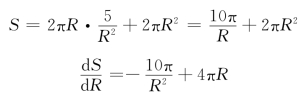
pagenumber_ebook=149,pagenumber_book=138

由解得唯一的驻点又由于制造固定容积的圆柱形密闭锅炉时，一定存在一个底半径，使锅炉的表面积最小.因此，当时，S（R）在该点取得最小值.此时，相应的高

即当圆柱形密闭锅炉的高与底直径都等于时，表面积最小，从而使用料最省.