高等数学上册：函数极值

2023-11-19 理论教育版权反馈

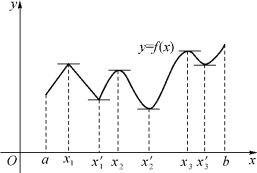
【摘要】：定义1凡是满足方程f′（x）＝0的点x称为函数f（x）的驻点.根据导数的几何意义，在曲线y＝f（x）上驻点处的切线是水平的.图3－9在图3－9中，考察函数f（x）在［a，b］上的极值与最值，发现：函数f（x）在点x1，x2，x3处取得极大值，函数f（x）在x′1，x′2，x′3处取得极小值；其最大值为f（b），最小值为f（x′2）.观察该图还发现：函数在一个区间内可以有若干个极大值与极小值，函数

定义1　凡是满足方程f′（x）＝0的点x称为函数f（x）的驻点.

根据导数的几何意义，在曲线y＝f（x）上驻点处的切线是水平的.

pagenumber_ebook=144,pagenumber_book=133

图3－9

在图3－9中，考察函数f（x）在［a，b］上的极值与最值，发现：函数f（x）在点x1，x2，x3处取得极大值，函数f（x）在x′1，x′2，x′3处取得极小值；其最大值为f（b），最小值为f（x′2）.观察该图还发现：函数在一个区间内可以有若干个极大值与极小值，函数在点x2处的极大值f（x2）比在x′3处的极小值f（x′3）还要小，这是因为我们讨论的函数极值是局部概念，只将它与该点左、右邻近的函数值比较，而最大值与最小值是在指定的某一区间上来考察的，是整体的、全局的最值.

函数的极值未必是指定区间上的最值.下面先讨论连续函数极值点的求法.

从图3－9中可以看出，在极值点处要么函数的导数为零（如x2，x′2，x3，x′3），要么其导数不存在（如x1，x′1）.因此函数在导数为零与导数不存在的点处都可能取得极值.

由3.1节中的费马定理可知，可导函数在极值点处的导数必为零，故有如下定理.

定理1（必要条件）　设函数f（x）在x0处可导，且在x0处取得极值，那么函数f（x）在x0处的导数f′（x0）＝0.

由定理1可知，在可导的前提下，极值点必是驻点，但驻点未必都是极值点.例如函数y＝x3，当x＝0时，y′＝3x2＝0，因此x＝0是函数y＝x3的驻点，但y＝x3是单调函数，故x＝0不是该函数的极值.因此f′（x0）＝0仅是一个可导函数f（x）在x0取得极值的必要条件，而非充分条件.因此定理1的另一个意思是说：可导函数的极值点必须从驻点中去寻求.

应当指出，在导数不存在的点处，函数也可能取得极值，例如函数f（x）＝｜x｜在x＝0处连续但不可导，然而x＝0是它的一个极小值.

综上所述，连续函数的极值点只可能是其驻点与不可导点，但它们未必是极值点.因此，把函数在定义区间内的驻点与不可导点统称为函数的可能极值点.

观察图3－9，可见函数的极值点必是其单调增加与单调减少区间的交界点.由此得到利用导数符号判定函数的极值的方法（也称为极值存在的充分条件）.

定理2（极值存在的充分条件一）　设函数f（x）在x0的某邻域U（x0，δ）内连续，且f′（x0）＝0或f′（x0）不存在，而在其去心邻域）内f（x）可导，如果

（1）当x∈（x0－δ，x0）时f′（x）＞0，x∈（x0，x0＋δ）时f′（x）＜0，那么f（x）在x0处取得极大值f（x0）.

（2）当x∈（x0－δ，x0）时f′（x）＜0，x∈（x0，x0＋δ）时f′（x）＞0，那么f（x）在x0处取得极小值f（x0）.

（3）当内时，f′（x）恒为正或恒为负，那么f（x）在x0处不取得极值.

证　（1）当x∈（x0－δ，x0）时，由于x＜x0，f′（x）＞0，故在x0的左侧邻近，f（x）是单调增加的，即有f（x）＜f（x0）；当x∈（x0，x0＋δ）时，由于x＞x0，f′（x0）＜0，则在x0的右侧邻近，f（x）是单调减少的，故有f（x）＜f（x0）.故x在x0的左、右两侧邻近时，恒有f（x）＜f（x0）成立，即f（x0）为f（x）的一个极大值.

（2），（3）同理可证.

证毕.

定理2告诉我们一个判定连续函数的可能极值点是否为极值点的方法，即只需看这些点的左、右两侧邻近的导数符号是否改变，导数符号改变的点就是极值点，在该点左、右两侧导数符号左正右负的点为极大值点，左负右正的点为极小值点，两侧邻近导数符号不改变的点就不是极值点.

因此定理2是判别函数的驻点与不可导点是否为极值点的常用方法.

例1　求函数的单调区间与极值.

解　 pagenumber_ebook=146,pagenumber_book=135 由y′＝0，解得由y′不存在，解得x2＝0，x3＝1.列表表示如下.

表3－4

pagenumber_ebook=146,pagenumber_book=135

由表3－4可知：函数的单调增加区间为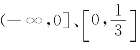 pagenumber_ebook=146,pagenumber_book=135 与［1，＋∞），单调减少区间为在x＝0的两侧邻近都有y′＞0，即y′在x＝0的两侧邻近不变号，因此x＝0不是y的极值点；在的两侧邻近y′的符号左正右负，故x＝是y的极大值点，且极大值在x＝1的两侧邻近y′的符号左负右正，因此x＝1是y的极小值点，且极小值y（1）＝0.

从上例可知，求极值的步骤可分为三步：

（1）求函数的导数.

（2）求导数的零点（即驻点）与不可导点即可疑极值点.

（3）确定可疑极值点的左、右两侧邻近的导数符号，从而判断并求出函数的极值.(www.chuimin.cn)

当函数在其驻点处的二阶导数易于计算且不为零时，有更简便的求极值的方法.

定理3（极值存在的充分条件二）　设f（x）在x0处具有二阶导数，且f′（x0）＝0，f″（x0）≠0，则：

（1）当f″（x0）＜0时，函数f（x）在x0处取得极大值.

（2）当f″（x0）＞0时，函数f（x）在x0处取得极小值.

证　（1）因为f″（x0）＜0，由二阶导数定义及定理条件得

由极限的局部保号性可知，∃使得时有

pagenumber_ebook=146,pagenumber_book=135

则当x渐渐增大经过点x0时，x－x0由负变正，故f′（x）相应地由正变负，由定理2可知，这时f（x0）为极大值.

（2）同理可证，当f″（x0）＞0时，f（x）在x0处取得极小值.

需要指出的是：在应用定理3时，首先要注意检验条件“x0是f（x）的驻点”是否成立；其次对于驻点x0，若有f″（x0）＝0，则x0可能是极大值点，也可能是极小值点，还可能不是极值点.例如，对于函数y＝－x4，y＝x4与y＝x3，由于它们在x＝0处都有y′（0）＝0，y″（0）＝0，因此都不能用定理3来判别，而根据定理2可知，这三个函数在x＝0处分别取得极大值、极小值和不取得极值.

例2　求f（x）＝x3－3x2－9x＋5的极值.

解　显然f（x）在（－∞，＋∞）处处连续、可导，有

f′（x）＝3x2－6x－9＝3（x－3）（x＋1）

由f′（x）＝0，解得x1＝－1，x2＝3.又

f″（x）＝6x－6＝6（x－1）

且

f″（－1）＝－12＜0，f″（3）＝12＞0

由定理3可知，f（－1）＝10是f（x）的极大值，f（3）＝－22是f（x）的极小值.

例3　设y＝f（x）由方程2y3－2y2＋2xy－x2＝1所确定，求函数y＝f（x）的极值.

解　原方程两边对x求导并整理，得

3y2　y′－2yy′＋xy′＋y－x＝0

令y′＝0，解得y＝x，将它代入原方程中，得