一、函数的单调性从图上可以直观地看出，单调增加函数的切线斜率非负（见图3-3），单调减少函数的切线斜率非正（见图3-4）.图3-3图3-4定理3.7 设函数f（x）在区间I内可导，则：1）对任意x∈I，有f′（x）＞0，则函数f（x）在I严格单调增加；2）对任意x∈I，有f′（x）＜0，则函数f（x）在I严格单调减少.证 先证1）对任意x1，x2∈I且x1＜x2，函数f（x）在区间[x1，x2]上......
2023-11-22
函数单调性-高等数学 上册
【摘要】：函数的单调性是函数的主要性质之一，下面利用导数来研究函数的单调性的判别方法.从图3－4（a）中可看出，当沿着单调增加函数的曲线从左向右移动时，曲线逐渐上升，它的切线的倾斜角α总是锐角，即这时斜率f′（x）＞0；从图3－4（b）中可看出，当沿着单调减少函数的曲线从左向右移动时，曲线逐渐下降，其切线的倾斜角α总是钝角，即这时斜率f′（x）＜0.图3－4从上面的几何直观中可得出：当函数在区间内是单调增加
函数的单调性是函数的主要性质之一，下面利用导数来研究函数的单调性的判别方法.
从图3－4（a）中可看出，当沿着单调增加函数的曲线从左向右移动时，曲线逐渐上升，它的切线的倾斜角α总是锐角，即这时斜率f′（x）＞0；从图3－4（b）中可看出，当沿着单调减少函数的曲线从左向右移动时，曲线逐渐下降，其切线的倾斜角α总是钝角，即这时斜率f′（x）＜0.
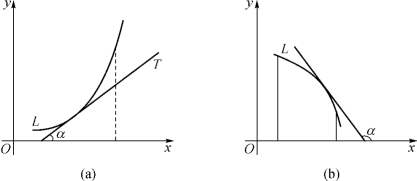
图3－4
从上面的几何直观中可得出：当函数在区间内是单调增加函数时，它在该区间内的导数恒为正；当函数在区间内是单调减少函数时，其导数在该区间内恒为负.由此我们猜想能否利用导数的符号来判别函数的单调性呢？根据微分中值定理，容易得到如下定理.
定理1 设函数f（x）在闭区间［a，b］上连续，在开区间（a，b）内可导，那么
（1）若在（a，b）内f′（x）＞0，则函数f（x）在［a，b］上严格单调增加.
（2）若在（a，b）内f′（x）＜0，则函数f（x）在［a，b］上严格单调减少.
证 （1）∀x1，x2∈（a，b），不妨设x1＜x2，由题设可知f（x）在［x1，x2］上连续、可导，即满足拉格朗日中值定理的条件，故∃ξ∈（x1，x2）⊂（a，b），使
f（x2）－f（x1）＝f′（ξ）（x2－x1） （x1＜ξ＜x2）
由题设中条件（1）可知，f′（ξ）＞0，故
f（x2）－f（x1）＞0
所以函数f（x）在［a，b］上严格单调增加.
（2）同理可证，当f′（x）＜0时，f（x）在［a，b］上严格单调减少.
从证明过程中容易看出：如果定理1中的闭区间换成了其他各种区间（包括无穷区间），那么结论也成立.另外必须指出，如果连续函数的可导性仅在有限个点处不成立，这时定理1的结论仍成立.
利用定理1可判别函数的单调性并确定其单调区间.
例1 讨论函数
的单调性.
解 f（x）在（－∞，＋∞）内连续且可导，对f（x）求导，得
f′（x）＝x2－2x＝x（x－2）
由f′（x）＝x（x－2）＝0，解得x1＝0，x2＝2，x1，x2将f（x）的定义域（－∞，＋∞）分成了三个部分区间，在每个部分区间上讨论函数的导数符号并根据导数符号判别其单调性.
当x∈（－∞，0）时，由于f′（x）＞0，故这时f（x）严格单调增加；当x∈（0，2）时，由于f′（x）＜0，故这时f（x）严格单调减少；当x∈（2，＋∞）时，由于f′（x）＞0，故这时f（x）严格单调增加.
综上所述，f（x）在区间（－∞，0］及［2，＋∞）上严格单调增加，在区间（0，2）内严格单调减少.
例2 讨论函数f（x）＝x3的单调性.
解 f（x）在（－∞，＋∞）内连续且可导，对f（x）求导，得
f′（x）＝3x2
可见，除了点x＝0使f′（x）＝0外，在其余各点处均有f′（x）＞0，因此函数f（x）在区间（－∞，＋∞）内严格单调增加（图3－5）.(www.chuimin.cn)
图3－5
例3 确定函数
的单调区间.
解 f（x）在（－∞，＋∞）内连续，对f（x）求导，得
由f′（x）＝0，解得
由f′（x）不存在，解得x＝0，x＝1.
因此
将（－∞，＋∞）分成四个部分区间，显然f′（x）的正负性取决于因式（3x－1）与（x－1）.下面列表讨论f′（x）在各部分区间内的符号（表3－1）.
表3－1
由表3－1可见，函数f（x）单调增加的区间为
与［1，＋∞），单调减少的区间为
一般地，若函数f（x）在定义区间上连续，且除去有限个导数不存在的点外，f（x）的导数均存在，这时可用导数为零的点和导数不存在的点将函数的定义区间划分成若干个部分区间，在各部分区间内f′（x）保持固定的符号，因而根据这些符号就可确定f（x）在每个部分区间上的单调性.利用函数的单调性还可证明一些不等式.
一般地，如果f（x）在（a，b）上恒有f′（x）≥0，则由定理1，可判定f（x）在［a，b］上单调增加，则当f（a）≥0时，就有f（x）＞f（a）≥0（x∈（a，b）），从而可证得不等式f（x）＞0成立.
例4 证明：当x≠0时，ex≥1＋x.
证 设f（x）＝ex－（1＋x），则函数f（x）在定义域（－∞，＋∞）上连续、可导，且f（0）＝0，因此只需证明：当x≠0时，有f（x）＞0即可.
对f（x）求导得：f′（x）＝ex－1，由f′（x）＝0，解得x＝0，故当x＜0时，f′（x）＜0，因此f（x）在（－∞，0）内严格单调递减，则当x＜0时，有
f（x）＞f（0）＝0
即
f（x）＞0
当x＞0时，f′（x）＞0，因此f（x）在（0，＋∞）内严格单调递增，则当x＞0时，有
f（x）＞f（0）＝0
即
f（x）＞0
综上可得：当x≠0时恒有f（x）＞0，即x≠0时，ex＞1＋x.
有关高等数学 上册的文章
- 详细阅读
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2023-11-19
-
高等数学上册：函数极值详细阅读
定义1凡是满足方程f′（x）＝0的点x称为函数f（x）的驻点.根据导数的几何意义，在曲线y＝f（x）上驻点处的切线是水平的.图3－9在图3－9中，考察函数f（x）在［a，b］上的极值与最值，发现：函数f（x）在点x1，x2，x3处取得极大值，函数f（x）在x′1，x′2，x′3处取得极小值；其最大值为f（b），最小值为f（x′2）.观察该图还发现：函数在一个区间内可以有若干个极大值与极小值，函数......
2023-11-19
-
高等数学上册：有理函数积分详细阅读
两个多项式的商称为有理函数，其中n和m是非负整数，且a0≠0，b0≠0.当n≥m≥1时，称式（4－5）所表示的函数为有理假分式函数；当n＜m时，称式（4－5）所表示的函数为有理真分式函数.当f是假分式时，利用多项式的除法，可将它化为一个多项式与一个真分式的和.例如，因此有理函数的积分问题可归结为求真分式的积分问题.1）有理函数的分解定理1设有真分式（4－5）式，若Qm＝b0（x－a）α…（x－b）βλ…......
2023-11-19
-
初等函数及其反函数-高等数学 上册详细阅读
1）反函数设函数y＝f（x）的定义域为D，值域为f（D），在函数y＝f（x）中，x为自变量，y为因变量，x可以独立取值，而y却按确定的法则随x而定，即函数y＝f（x）反映的是y怎样随x而定的法则；反过来，对于y∈f（D），若D内总有确定的x与之对应，使得f（x）＝y成立，这样得到一个以y为自变量，x为因变量的函数，称该函数为y＝f（x）的反函数，记作x＝f－1（y），其定义域为f（D），值域为D.......
2023-11-19
-
高等数学上册：函数间断点详细阅读
有的曲线在定义域上不是处处连续的，而会在某些点处断开，例如函数y＝它在x＝0时无定义，其图形在该点处断开；又如函数y＝tanx，它在x＝kπ＋时无定义，其图形在这些点处断开；又如取整函数y＝［x］，它在整数点处都有定义，但其图形在这些点处都是断开的.观察发现曲线上断开的这些点处都具有如下特征：函数在该点的邻近有定义，但在该点处不连续.将这类点称为函数的间断点.定义4设函数f（x）在点x0的某去心......
2023-11-19
-
高等数学基础：中值定理和函数单调性详细阅读
一、拉格朗日（Lagrange）中值定理定理1（拉格朗日中值定理）若函数f（x）满足条件：（1）在闭区间[a，b]上连续；（2）在开区间（a，b）内可导；则至少存在一点ξ∈（a，b），使得或图3.1拉格朗日中值定理的几何意义：如果在闭区间[a，b]上连续的一条曲线弧y=f（x）除端点外处处具有不垂直于x轴的切线，则曲线上至少存在一点C，使得曲线在点C处的切线平行于连接曲线两端点的弦AB.显然，......
2023-11-20
-
高等数学上册：变上限积分函数及导数探究详细阅读
设y＝f（x）在［a，b］上连续，且x0∈［a，b］.设Φ（x0）表示由曲线y＝f（x）、x轴、直线x＝a和x＝x0所围平面图形面积的代数和.显然，由定积分的概念可知Φ（x0）一定存在，且其大小只与x0有关，与积分变量x无关.为明确起见，用t做积分变量，将x0换成x，从而给出积分函数的定义.定义1设函数f（x）在［a，b］上可积，x∈［a，b］，则函数是上限变量x的函数，称为变上限积分函数，记作......
2023-11-19
相关推荐