首页理论教育洛必达法则：无穷小比的极限

洛必达法则：无穷小比的极限

2023-11-19 理论教育版权反馈

【摘要】：先给出两个无穷小之比的极限的洛必达法则.定理1（洛必达法则）如果函数f（x），g（x）满足：①②在x0的某个去心邻域内，f′（x），g′（x）都存在，且g′（x）≠0；③存在（或为无穷大），则证因为极限与函数f（x），g（x）在x＝x0处的值无关，所以不妨重新定义f（x0）＝g（x0）＝0，则在x＝x0处重新定义后的函数f（x），g（x）在x0处连续，设x是x0的去心邻域内的任一点，再由条件①

先给出两个无穷小之比的极限的洛必达法则.

定理1（洛必达法则）　如果函数f（x），g（x）满足：

①

②在x0的某个去心邻域内，f′（x），g′（x）都存在，且g′（x）≠0；

③存在（或为无穷大），

则

证　因为极限与函数f（x），g（x）在x＝x0处的值无关，所以不妨重新定义f（x0）＝g（x0）＝0，则在x＝x0处重新定义后的函数f（x），g（x）在x0处连续，设x是x0的去心邻域内的任一点，再由条件①、②可知，在x＝x0处重新定义后的函数f（x），g（x）在以x0，x为端点的闭区间上，满足柯西中值定理的条件，故

其中ξ介于x0与x之间.对上式求x→x0时的极限，由于当x→x0时，必有ξ→x0，再由条件③，得

定理1说明，当存在时也存在，且等于当 pagenumber_ebook=125,pagenumber_book=114 为无穷大时也为无穷大，这种在一定条件下利用公式（3－7）来求极限的方法称为洛必达（L'Hospital）法则.

必须指出，若型，且f′（x），g′（x）仍能满足定理1中的条件①、②、③，则对f′（x），g′（x）可继续用洛必达法则，得

且可以此类推下去.

例1　计算

解　 pagenumber_ebook=126,pagenumber_book=115

例2　计算

解　　

例3　计算

解

例4　计算

解(www.chuimin.cn)

必须指出，满足定理1的条件的型未定式可用洛必达法则求解，并可连续多次应用，直到不符合定理1的条件为止；当不是未定式的极限时就不能用洛必达法则求解.另外用该法则求极限时，可综合运用以前学过的方法，使计算过程更简单.

例5　计算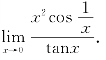 pagenumber_ebook=126,pagenumber_book=115

解　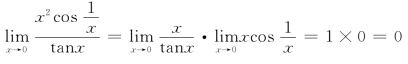 pagenumber_ebook=127,pagenumber_book=116

注　该题不能用洛必达法则求解，因为用洛必达法则计算时，

由于极限不存在，故不能用洛必达法则求该极限，即这时洛必达法则失效.

从例5可知，洛必达法则的条件是充分的而不是必要的，当不存在（不包括∞）时，虽不能应用洛必达法则求解，但这时极限仍可能存在，不过应使用其他方法求解.

对x→∞时的型未定式，也有类似的洛必达法则.

只要令则当x→∞时，有t→0，则

由此可得如下定理.

定理2　如果函数f（x），g（x）满足：

①

②∃X，当｜x｜＞X时，f′（x），g′（x）都存在，且g′（x）≠0；

③存在（或为无穷大），

则

需要指出的是应用定理2时有与应用定理1同样的注意事项.

例6　计算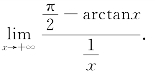 pagenumber_ebook=128,pagenumber_book=117

解　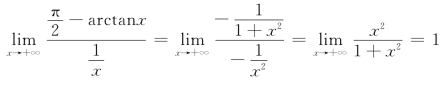　 pagenumber_ebook=128,pagenumber_book=117