1）几个实际问题（1）平面曲线的切线问题设点M0（x0，y0）与M（x，y）分别是平面曲线y＝f（x）上的一个定点与动点，则割线MM0的斜率为根据切线的定义可知，当M→M0，即Δx→0时，若存在，则该极限就等于切线的斜率，即因此曲线y＝f（x）在点M0（x0，y0）处的切线方程为y－y0＝k（x－x0）（2）变速直线运动的瞬时速度问题设质点M沿某直线作s＝s（t）的变速直线运动，s（t）为t时刻质......
2025-09-30
拉格朗日中值定理-高等数学 上册
【摘要】：取消罗尔定理中关于“函数在两端点处的函数值必须相等”的条件，就可得到一般情形下的微分中值定理，也称为拉格朗日中值定理.定理3（拉格朗日中值定理）若y＝f（x）在［a，b］上连续，在（a，b）内可导，则ξ∈（a，b），使得证设辅助函数则定理2的结论可写成下面验证函数F（x）在［a，b］上满足罗尔定理的三个条件.由于f（x）在［a，b］上连续，在（a，b）内可导，故F（x）在［a，b］上连续，在（
取消罗尔定理中关于“函数在两端点处的函数值必须相等”的条件，就可得到一般情形下的微分中值定理，也称为拉格朗日中值定理.
定理3（拉格朗日中值定理） 若y＝f（x）在［a，b］上连续，在（a，b）内可导，则∃ξ∈（a，b），使得
证 设辅助函数
则定理2的结论可写成
下面验证函数F（x）在［a，b］上满足罗尔定理的三个条件.
由于f（x）在［a，b］上连续，在（a，b）内可导，故F（x）在［a，b］上连续，在（a，b）内可导.又
即
F（a）＝F（b）
所以F（x）在［a，b］上满足罗尔定理的三个条件.因此，由罗尔定理可知，∃ξ∈（a，b），使得F′（ξ）＝0，即
证毕.
上面的式（3－3）也常常写成
f（b）－f（a）＝f′（ξ）（b－a） （3－4）
若设a＝x0，b＝x0＋Δx，则式（3－3）可以表达为
f（x0＋Δx）－f（x0）＝f′（x0＋θΔx）·Δx （0＜θ＜1） （3－5）
或
Δy＝f′（x0＋θΔx）·Δx （0＜θ＜1） （3－6）
拉格朗日中值定理实际上是罗尔定理的推广形式，也是微分学中十分重要的定理，因此又称为微分中值定理.由于式（3－6）的表达形式为增量形式，拉格朗日中值定理也称为有限增量公式.
由于
表示曲线两端连线的斜率，故拉格朗日中值定理的几何意义是：若连续曲线段
上各点都有不垂直于x轴的切线，则在曲线上必存在一点C，该点处的切线平行于曲线两端的连线段
（图3－2）.
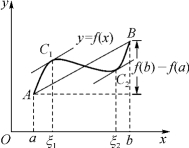
图3－2(https://www.chuimin.cn)
与罗尔定理一样，拉格朗日中值定理只确定了中值ξ的存在性，对于不同的函数，ξ的具体位置一般是不同的.当定理中的条件不成立时，结论就不一定成立.
推论 若函数f（x）在区间I上的导数恒为0，则f（x）在I上是一个常数函数.
证 设∀x1，x2∈I，且x1＜x2，由题设可知，f（x）在［x1，x2］上连续，在（x1，x2）内可导，则f（x）在［x1，x2］上可应用拉格朗日中值定理，即∃ξ∈（x1，x2），使得
f（x2）－f（x1）＝f′（ξ）（x2－x1）
由题设可知f′（ξ）＝0，故
f（x2）－f（x1）＝0
再由x1，x2的任意性可知，f（x）在I上的函数值总是相等的，即为常数.
例4 证明：x∈［0，1］时，恒有
证 令
则f（x）在［0，1］上连续，在（0，1）内可导，又
由推论可知：当
又
故
例5 证明：当x＞0时，不等式
成立.
证 令f（x）＝ln（1＋x），则f（x）在［0，x］（x＞0）上连续、可导，且
由拉格朗日中值定理可知，存在一个ξ∈（0，x），使得
由于
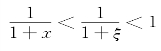
所以
相关文章
- 详细阅读
-
高等数学上册：极限性质详细阅读
利用函数极限的定义，可得下列极限的性质.1）唯一性定理2若存在，则极限唯一.证（反证法）假设极限不唯一，则存在两个不相等的常数a，b，使得均成立.不妨设b＞a，由于取则δ1＞0，当x满足0＜｜x－x0｜＜δ1时，恒有即又由于仍取则δ2＞0，当x满足0＜｜x－x0｜＜δ2时，恒有即取δ＝min｛δ1，δ2｝，则当x满足0＜｜x－x0｜＜δ时，上面（1－5）、（1－6）两式均成立，但这是不可能的.......
2025-09-30
-
数列极限：高等数学上册详细阅读
对于给定的数列｛xn｝，我们讨论当项数n无限增大时（记作n→∞），对应项的变化趋势.观察上面的四个数列，容易看出，当n→∞时，数列趋于1；数列各项的值在数1的两侧来回交替着变化，且越来越接近1；数列｛2n－1｝越来越大，无限增大；数列｛1－（－1）n｝各项的值永远在0与2之间交互取得，而不与某一数接近.如果当n→∞时，数列的项xn能无限接近于某个常数A，则称这个数列为收敛数列，常数A称为当n→∞时......
2025-09-30
-
无穷小量比较：高等数学上册详细阅读
我们已经知道两个无穷小量的和、差、积仍为无穷小，但两个无穷小量的商的情形就较为复杂，例如下面几个简单的无穷小量的商的极限：从上面三个极限中就看出：虽然当x→0时，x3，x2，x，1－cosx都是无穷小，但它们比值的极限却有着各自不同的情形，分析这些情形产生的原因，发现是由于各个无穷小趋于零的快慢程度不同而造成的.就上面的例子来说，在x→0的过程中，x2→0的速度比x→0要快，x2→0的速度比x3→......
2025-09-30
-
无穷小的定义-高等数学 上册详细阅读
定义1若则称函数f（x）为当x→□时的无穷小量，简称无穷小.特别地，若则称数列｛xn｝是n→∞时的无穷小.例如，由于所以函数是x→∞时的无穷小；由于所以常数0可以看作任意变化过程时的无穷小；由于所以数列是n→∞时的无穷小.应当指出无穷小是对应特殊变化过程时的变量或函数，不能将它与绝对值很小很小的固定常数混为一谈.任何非零常数无论其绝对值多么小，都不是无穷小.由于零的极限是零，所以零是唯一可以作为......
2025-09-30
-
高等数学上册：单调有界准则详细阅读
定义1称满足条件xn≤xn＋1（n＝1，2，…）即｛xn｝单调增加.下面再证｛xn｝上有界：由xn的展开式可知即｛xn｝上有界.因此该数列｛xn｝单调增加且有上界，由准则Ⅱ可知，极限存在，将该极限用字母e表示，即可证明e是一个无理数，且2＜e＜3，它的值为e＝2.718 281 828 459 045…......
2025-09-30
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2025-09-30
-
初等函数及其反函数-高等数学 上册详细阅读
1）反函数设函数y＝f（x）的定义域为D，值域为f（D），在函数y＝f（x）中，x为自变量，y为因变量，x可以独立取值，而y却按确定的法则随x而定，即函数y＝f（x）反映的是y怎样随x而定的法则；反过来，对于y∈f（D），若D内总有确定的x与之对应，使得f（x）＝y成立，这样得到一个以y为自变量，x为因变量的函数，称该函数为y＝f（x）的反函数，记作x＝f－1（y），其定义域为f（D），值域为D.......
2025-09-30
相关推荐