在恩斯特·库默尔的工作之后，发现费马大定理证明的希望比以前更渺茫了，人们开始怀疑这个问题是不可能解决的，或许费马本来就是自己骗自己，没有人重新发现费马的证明就是因为根本不存在这样的证明，数学家纷纷转向其他不同的研究领域，新一代的数学家也极力避免那些似乎不可能解决、进入死胡同的危险，到20世纪初，这个问题虽然依然在数论家的心目中占有特殊的地位，但是他们对待费马大定理就像化学家对待炼金术一样，他们仿佛......
2023-11-19
罗尔定理的证明和费马定理的基本性质
【摘要】：从几何上可以看到：在对于两端高度相等的连续光滑曲线上，必存在一条水平的切线（如图3－1所示），这便是罗尔定理.为了罗尔定理证明的需要，下面先给出极值的定义和极值点的一条基本性质——费马定理.图3－1定义1设f（x）在点x0的某邻域内有定义，若x∈（x0，δ），恒有f（x）＜f（x0）（或f（x）＞f（x0）），则称f（x0）为f（x）的一个极大值（或极小值），函数的极大值与极小值统称为函数的极值
从几何上可以看到：在对于两端高度相等的连续光滑曲线上，必存在一条水平的切线（如图3－1所示），这便是罗尔定理.为了罗尔定理证明的需要，下面先给出极值的定义和极值点的一条基本性质——费马定理.
图3－1
定义1 设f（x）在点x0的某邻域内有定义，若∀x∈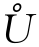
（x0，δ），恒有f（x）＜f（x0）（或f（x）＞f（x0）），则称f（x0）为f（x）的一个极大值（或极小值），函数的极大值与极小值统称为函数的极值，使函数取得极值的点x0称为函数的极值点.
下面给出极值点的一个必要条件.
定理1（费马定理） 设函数f（x）在（a，b）内可导，x0为f（x）在（a，b）内的一个极大（极小）值点，则f′（x0）＝0.
证 设x0为f（x）在（a，b）内的一个极大值点，取x0＋Δx∈（a，b），则
f（x0＋Δx）－f（x0）≤0
因此
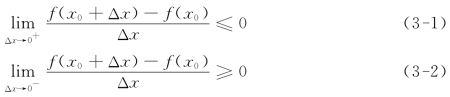
由题设，f（x）在x0点处可导，则
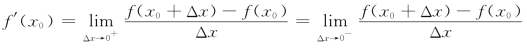
再根据（3－1）、（3－2）两式，得
f′（x0）＝0
同理可证，当f（x）在x0点处取得极小值时，也有f′（x0）＝0.
综上结论成立.
该定理表明：可导函数f（x）在点x0处取得极值的必要条件是f′（x0）＝0.
定理2（罗尔定理） 设函数y＝f（x）满足：
①在闭区间［a，b］上连续；
②在开区间（a，b）内可导；
③且f（a）＝f（b），
则至少在（a，b）内存在一点ξ，使得
f′（ξ）＝0
证 因为y＝f（x）在［a，b］上连续，所以由闭区间上连续函数的性质可知，函数y＝f（x）在［a，b］上必存在最大值M与最小值m.
（1）若M＝m，则在闭区间［a，b］上，有
M＝m＝f（a）＝f（b）＝f（x）
因此∀x∈（a，b），恒有f（x）≡M，故
f′（x）＝0
结论成立.
（2）若M≠m，由于f（a）＝f（b），因此M与m中至少有一个在区间（a，b）内取得.不妨设最大值M在区间（a，b）内的ξ点处取得，即f（ξ）＝M，则f（ξ）为f（x）在（a，b）内的一个极值点，又f（x）在（a，b）内可导，由费马定理可知：
f′（ξ）＝0(www.chuimin.cn)
故结论成立.
证毕.
必须指出：罗尔定理仅给出了ξ的存在性，指出了ξ的一个大概范围为ξ∈（a，b），并没有给出ξ的准确位置.
罗尔定理的几何意义（图3－1）为：两端点值相等的连续光滑曲线弧段上，至少有一点的切线平行于x轴（或弧上至少有一条水平切线）.
例1 对函数y＝x2－2x＋1在闭区间［0，2］上验证罗尔定理.
解 由于函数y＝x2－2x＋1在闭区间［0，2］上连续、可导，又
y（0）＝y（2）＝1
因此函数y在闭区间［0，2］上满足罗尔定理的三个条件.
事实上，y′＝2x－2，当ξ＝1时，有
f′（ξ）＝0
显然ξ∈（0，2），因此，罗尔定理对函数y＝x2－2x＋1在闭区间［0，2］上成立.
利用罗尔定理可以讨论方程f′（x）＝0的根的存在性以及证明一类形如“f′（ξ）＝0”的存在性命题，下面举例说明.
例2 证明方程4ax3＋3bx2＋2cx－a－b－c＝0至少有一个正根，其中a，b，c是任意常数.
证 构造函数
f（x）＝ax4＋bx3＋cx2－（a＋b＋c）x
显然f（x）在闭区间［0，1］上连续，又在（0，1）内可导，且f（0）＝0＝f（1），根据罗尔定理可知，存在ξ∈（0，1），使得f′（ξ）＝0，即
4aξ3＋3bξ2＋2cξ－a－b－c＝0
结论得证.
例3 设函数f（x）与g（x）均在［a，b］上连续，在（a，b）内可导，且
f（b）－f（a）＝g（b）－g（a）
试证：在（a，b）内至少存在一点c，使得f′（c）＝g′（c）.
证 令F（x）＝f（x）－g（x），由题意可知，F（x）在［a，b］上连续，在（a，b）内可导，又由
f（b）－f（a）＝g（b）－g（a）
得
f（b）－g（b）＝f（a）－g（a）
即
F（b）＝F（a）
由罗尔定理可知，∃c∈（a，b），使得F′（c）＝0成立，即
f′（c）＝g′（c）
有关高等数学 上册的文章
- 详细阅读
- 详细阅读
-
高等数学（上、下册）：罗尔定理及应用详细阅读
一、罗尔定理定理3.1 若函数f（x）满足条件：1）在[a，b]上连续；2）在（a，b）内可导；3）在区间端点处的函数值相等，即f（a）=f（b）；则在（a，b）内至少存在一点ξ，使得f′（ξ）=0.证 如图3-1所示，因为f（x）在[a，b]上连续，由连续函数的性质，f（x）在[a，b]上必有最大值M和最小值m.1）如果m=M，则f（x）在[a，b]上恒为常数M，因此在（a，b）内恒有f（x）=......
2023-11-22
-
费马大定理的突破与谷山-志村猜想的关联详细阅读
自费马1637年左右提出“费马大定理”，三百多年过去了，数学界一直未能找到一个解决它的方法，1984年，数学家G.弗莱提出了一个引人注目的论断：如果有人能够证明谷山-志村猜想，那么他们也就自动证明了费马大定理.谷山丰和志村五郎是日本东京大学两位极具才华的数学家，他们研究的内容属现代数学中最深奥的领域，分别是椭圆曲线和模型式.椭圆曲线是指以下形式的任何方程y2=x3+ax2+bx+c（a，b，c为整......
2023-11-19
-
微积分基本定理：积分和求导互逆详细阅读
而有趣的是，导数和积分其实是紧密相关的。给定一个函数，通过对它进行求导，我们能得出另外一个函数，后者可以表示前者在每一点处的变化情况。微积分基本定理大致讲的是，先取一个函数f，对它进行求导，得出一个新函数，接着对这个新函数进行积分，你会再次得到f。换句话讲，积分和微分是互逆的过程。求导和求积分互为逆运算。......
2023-11-22
-
2页纸图解数学:极聪明方式解决费马最后定理详细阅读
费马最后定理说的是，这些更大的n值所对应的方程都不存在解！参考阅读//No. 14 自然数，第32页No. 43 伽罗瓦理论，第90页No. 44 丢番图方程，第92页3.一分钟记忆虽然费马最后定理只是一个没有什么实际应用性的纯数学问题，但是我们在证明它的过程中发展出被广泛应用的新理念和新技巧。......
2023-11-22
-
正交子空间定理及证明详细阅读
定义6.6 若V1和V2是欧氏空间V的子空间，且对任意的α∈V1，β∈V2，总有<α，β>=0，则称子空间V1与V2是正交的.如果同时还有V1⊕V2=V成立，则V2就称为V1的正交补空间，记作V2=V1⊥.同样地，此时V1也是V2的正交补空间.定理6.3n维欧氏空间的任意子空间都有唯一的正交补空间.证明：设W是n维欧氏空间V的一个子空间，如果W是零维的，无须证明.现设dimW>0，选取W的一组正交基α1，α2，…......
2023-11-22
-
毕达哥拉斯定理的发现和证明，以及其背后的故事详细阅读
据传毕达哥拉斯学派为庆祝该定理的发现曾宰杀百牛祭祀缪斯女神,但这与该学派所奉行的素食主义相悖。后人对毕达哥拉斯发现和证明勾股定理有各种猜测。图3.2.14毕达哥拉斯定理图3.2.15毕达哥拉斯定理的证明一般认为,毕达哥拉斯采用了剖分方法来证明定理。因而就有化简后则得到毕达哥拉斯定理。《几何原本》中的毕达哥拉斯定理图3.2.16毕达哥拉斯纪念碑3.2.17《几何原本》命题473.2.18希腊1955 年邮票毕达哥拉斯定理是《几何原本》第一卷命题47。......
2023-11-23
相关推荐