首页理论教育微分运算法则-高等数学上册

微分运算法则-高等数学上册

2023-11-19 理论教育版权反馈

【摘要】：由函数的和、差、积、商的求导法则，结合公式（2－46）可推得相应的微分运算法则，为了便于对照，列于表2－2中.表2－2函数的求导法则与微分法则下面仅以乘积的微分法则为例加以证明.由函数微分公式（2－46），有d（uv）＝（uv）′dx＝（u′v＋uv′）dx＝u′dx·v＋u·v′dx＝vdu＋udv因此d（uv）＝vdu＋udv其他法则均可类似证明.请读者自证.下面讨论复合函数的微分.设函数y

由函数的和、差、积、商的求导法则，结合公式（2－46）可推得相应的微分运算法则，为了便于对照，列于表2－2中.

表2－2　函数的求导法则与微分法则

pagenumber_ebook=114,pagenumber_book=103

下面仅以乘积的微分法则为例加以证明.

由函数微分公式（2－46），有

d（uv）＝（uv）′dx＝（u′v＋uv′）dx＝u′dx·v＋u·v′dx＝vdu＋udv

因此

d（uv）＝vdu＋udv

其他法则均可类似证明.请读者自证.

下面讨论复合函数的微分.

设函数y＝f（u）可微，则dy＝f′（u）du.

若上式中u是中间变量，函数u＝φ（x）可微，则复合函数y＝f［φ（x）］也可微，其微分(www.chuimin.cn)

dy＝（f［φ（x）］）′dx＝f′［φ（x）］·φ′（x）·dx＝f′（u）du

可见，当u是中间变量时，dy也可表达为f′（u）du，与u是自变量时，在形式上是相同的.这个性质称为微分形式的不变性.它在微分的运算中很有用：在计算复合函数的微分时，可以把复合函数f［φ（x）］中的φ（x）当作一个整体变量直接对它求导，然后再求出φ（x）的微分即可.例如

d（sin2x）＝（cos2x）d（2x）＝2cos2xdx

例4　求的微分.

解　解法1

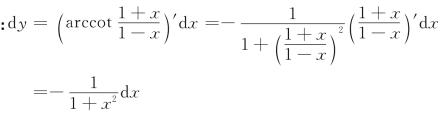
pagenumber_ebook=114,pagenumber_book=103

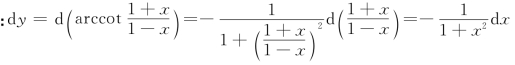
解法2 pagenumber_ebook=114,pagenumber_book=103

例5　求y＝x2lnx的微分.

解　解法1：dy＝（x2lnx）′dx＝（2xlnx＋x）dx

解法2