首页理论教育微分的概念及应用-高等数学上册

微分的概念及应用-高等数学上册

2025-09-30 理论教育版权反馈

【摘要】：先考察一个实例.例1有一块正方形金属薄片，因环境温度发生了微小的的变化，其边长从x0变为x0＋Δx，问薄片的面积将改变多少？

先考察一个实例.

例1　有一块正方形金属薄片，因环境温度发生了微小的的变化，其边长从x0变为x0＋Δx，问薄片的面积将改变多少？

解　设金属薄片的边长为x，则其面积A＝x2，当边长在x0处改变了Δx时，对应面积的改变量为

从上式可看出，ΔA由两部分组成，一部分是Δx的线性函数2x0Δx，即图2－2中带有斜阴影线的两个矩形面积之和；另一个是（Δx）2，即图2－2中带有交叉斜线的小正方形的面积.当｜Δx｜很小时，2x0Δx是ΔA的主要部分，而当Δx→0时，（Δx）2是比Δx高阶的无穷小.可见，用2x0Δx作为ΔA的近似值时，其误差达到（Δx）2，它是o（Δx），因此

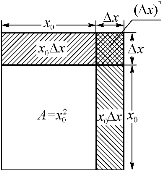
pagenumber_ebook=110,pagenumber_book=99

图2－2

ΔA≈2x0Δx

为了方便，数学上把这个近似代替函数改变量ΔA的线性部分2x0Δx称为该函数的微分.由此给出如下函数微分的定义.

定义1　设y＝f（x）在x0的某邻域U（x0）内有定义，Δx为自变量x的增量，且x0＋Δx∈U（x0），若相应函数的增量Δy＝f（x0＋Δx）－f（x0）可表示为

其中A（x0）是与Δx无关的常量，则称函数y＝f（x）在点x0可微，其中的关于Δx的线性部分A（x0）Δx称为函数y＝f（x）在x0处的微分，记作即

下面利用函数在点x0处可微及可导的定义推出函数可微的等价条件以及微分公式.

定理1　函数y＝f（x）在x0处可微的充要条件是y＝f（x）在x0处可导，且

证　（1）先证充分性.

设函数y＝f（x）在点x0处可导，即

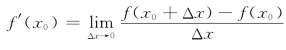
pagenumber_ebook=111,pagenumber_book=100

则

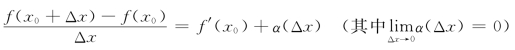
pagenumber_ebook=111,pagenumber_book=100

由此

Δy＝f（x0＋Δx）－f（x0）＝f′（x0）Δx＋Δx·α（Δx）

上式中f′（x0）是与Δx无关的一个量，且Δx·α（Δx）＝o（Δx），故y＝f（x）在点x0处可微，且

（2）再证必要性.

设函数y＝f（x）在点x0处可微，则存在与Δx无关的量A，使

Δy＝AΔx＋ο（Δx）

故(https://www.chuimin.cn)

则有

即y＝f（x）在点x0处可导，且f′（x0）＝A.因而有

证毕.

对于函数y＝x，由于y′＝1，则其微分为dx＝Δx，因此常把dx称为自变量x的微分，因此函数y＝f（x）的微分公式常写为

dy＝f′（x）dx　　（2－46）

例如，函数y＝sinx的微分为

dy＝cosxdx

需要指出，在微分公式（2－46）中，dy，f′（x），dx是三个具有独立意义的量，因此由微分公式（2－46）可得

上式将导数f′（x）看作微分dy与dx的商，所以导数也称为微商.

应当注意，微分与导数虽然有等价关系，却是有区别的：导数是函数在一点处的变化率，而微分是函数在一点处的自变量的增量所引起的函数的改变量的近似值；另外导数的值只与x有关，而微分的值与x和Δx都有关.

设y＝f（x）在x的集合I内每一点都可导，我们结合导数的基本公式，再利用微分与导数的关系式（2－46），就可得到求微分的基本公式.为了便于对照，表2－1中列出了基本初等函数的导数与微分公式.

表2－1　基本初等函数的导数与微分公式

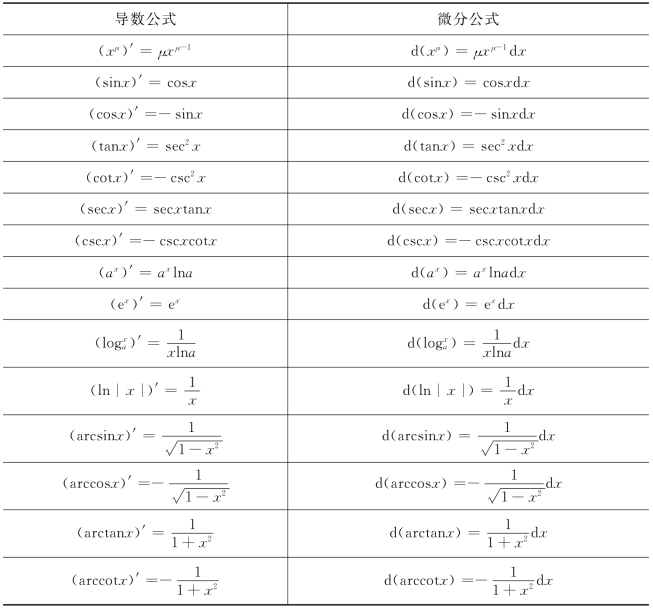
pagenumber_ebook=112,pagenumber_book=101

由定理1及公式（2－46）可知求微分的步骤为：先求函数的导数f′（x），再写出其微分为

dy＝f′（x）dx

例2　求y＝x3，当x＝4，Δx＝0.01时的微分.

解　由于y′＝3x2，故

dy＝3x2·Δx

将x＝4，Δx＝0.01代入上式得

例3　求函数的微分.

解　由于故