一、高阶导数在变速直线运动中,位置函数s=s对时间t的导数是速度函数v=v,而v=v对t的导数就是加速度,即加速度是位置函数的导数的导数.这种导数的导数称为s=s对时间t的二阶导数.一般地,如果函数y=f的导数仍是x的可导函数,那么y′=f′的导数,就叫作原来的函数y=f的二阶导数,记作即类似地,二阶导数的导数叫三阶导数,三阶导数的导数叫四阶导数,…......
2023-11-20
1)参数方程确定的函数的导数
有时函数由参数方程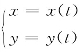 来表示更方便且简单,如
来表示更方便且简单,如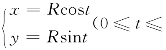 π)表示以R为半径、原点为圆心的上半圆周曲线
π)表示以R为半径、原点为圆心的上半圆周曲线![]() .星形线的直角坐标方程为
.星形线的直角坐标方程为![]() 其参数方程为
其参数方程为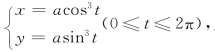 显然星形线的参数方程更为简单.
显然星形线的参数方程更为简单.
一般地,设参数方程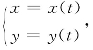 若t∈(α,β)时,x=x(t),y=y(t)都有连续的导数,且x′(t)≠0,可以证明x=x(t)必有单值反函数t=t(x),代入y=y(t)中,得y=y[t(x)],因此在所给条件下,参数方程
若t∈(α,β)时,x=x(t),y=y(t)都有连续的导数,且x′(t)≠0,可以证明x=x(t)必有单值反函数t=t(x),代入y=y(t)中,得y=y[t(x)],因此在所给条件下,参数方程 确定了y是x的函数y=y[t(x)],它必定可导,由复合函数与反函数的求导法则,求得其导数为
确定了y是x的函数y=y[t(x)],它必定可导,由复合函数与反函数的求导法则,求得其导数为
称上式为参数方程确定的函数的导数公式.
例6 求摆线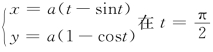 时的切线方程.
时的切线方程.
解 将![]() 代入参数方程中,得
代入参数方程中,得![]() 又
又
则![]() 因此摆线在
因此摆线在![]() 时的切线方程为
时的切线方程为
即(www.chuimin.cn)
2)参数方程确定的函数的二阶导数
显然参数方程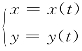 的导函数
的导函数![]() 仍是参数t的函数,因此其导函数
仍是参数t的函数,因此其导函数![]() 仍然可用参数方程表示:
仍然可用参数方程表示:
设x=x(t),y=y(t)都有连续的二阶导数,且x′(t)≠0,则利用参数方程的求导公式可得参数方程确定的函数的二阶导数为:
必须指出式(2-44)虽然可以作为参数方程![]() 确定的函数的二阶导数公式,但使用它并不方便,而用参数方程的求导方法求二阶导数如下:
确定的函数的二阶导数公式,但使用它并不方便,而用参数方程的求导方法求二阶导数如下:
该方法不仅更为方便,还可以用它求该参数方程确定的函数的更高阶的导数.
例7 设
解
有关高等数学 上册的文章

一、高阶导数在变速直线运动中,位置函数s=s对时间t的导数是速度函数v=v,而v=v对t的导数就是加速度,即加速度是位置函数的导数的导数.这种导数的导数称为s=s对时间t的二阶导数.一般地,如果函数y=f的导数仍是x的可导函数,那么y′=f′的导数,就叫作原来的函数y=f的二阶导数,记作即类似地,二阶导数的导数叫三阶导数,三阶导数的导数叫四阶导数,…......
2023-11-20

一、高阶导数一般地,若函数y=f的导数y′=f′仍然可导,这个导数就称为原来函数y=f的二阶导数,记作y″,f″或.类似地,若y″=f″的导数存在,称为y=f的三阶导数,记作y,f或.一般地,如果y=f的(n-1)阶导数y(n-1)=f(n-1)的导数存在,其导数就称为y=f的n阶导数,记作y,f或.二阶和二阶以上的导数统称为高阶导数.例1 求n次多项式y=a0xn+a1xn-1+…......
2023-11-22

由于初等函数是由基本初等函数经过有限次四则运算及有限次函数复合而构成的用一个解析式表示的函数,因此结合前面的求导法则与求导公式可推得:初等函数在其定义区间上处处可导,其导函数只要按照函数的结构,利用相应的求导公式或法则就可求出.例10求下列函数的导数:解(1)y′=e2t+t·2e2t=(1+2t)e2t.(2)由于故例11设求F′(x).解当x≠1时,F(x)在相应的定义区间上都是初等函......
2023-11-19

【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式:(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,(4),特别地,,(5)(sinx)′=cosx, (6)(cosx)′=-sinx,(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,(9)(secx)′=secx......
2023-10-27

解析函数不仅有一阶导数,而且有各高阶导数,它的值也可以用函数在边界上的值通过积分来表示.但是对于一元实函数来说,它在某一区间上可导,其导数在这区域上是否连续也不一定,更不要说它有高阶导数存在了.关于解析函数的高阶导数我们有下面的定理.定理2 解析函数f(z)的导数仍为解析函数,它的n阶导数为其中C为在函数f(z)的解析区域D内围绕z0 的任何一条正向简单闭曲线,而且它的内部全含于D.证明 设z0为......
2023-10-30

在某些问题中,可以用调用函数自身的方式来解决问题。在一个函数中直接或间接地调用该函数自身的方式称做函数的递归调用。递归的概念在我们的自然生活中并不陌生。讲的故事又是其自身,这就相当于递归。这也是递归的例子。在数学中,更是有许多函数采用递归的定义形式。=3628800函数fact()包含了对其自身的调用,因此fact()是一个递归函数。来看一看这个递归函数的执行过程。图5.6递归求解3!......
2023-11-18

【主要内容】设二元函数u=u(x,y),v=v(x,y)在点(x,y)处偏导数存在,函数z=f(u,v)在对应点(u,v)处可微,则复合函数z=f(u(x,y),v(x,y))在点(x,y)处的偏导数存在,且二元以上复合函数的偏导数也有类似的计算公式.注 在计算二元或二元以上复合函数的偏导数时,应先画出复合函数的关系图,然后按此图用复合函数求偏导数公式计算.例如,二元复合函数z=f(u(x,y),......
2023-10-27

复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε >0,相应地存在δ(ε)>0,使得当0 <|△z|<δ时,有若函数w =f(z)在区域D内......
2023-10-30
相关推荐