表示常量，用字母x，y，z，t，…......
2025-09-30
高数上：初等函数导数
【摘要】：由于初等函数是由基本初等函数经过有限次四则运算及有限次函数复合而构成的用一个解析式表示的函数，因此结合前面的求导法则与求导公式可推得：初等函数在其定义区间上处处可导，其导函数只要按照函数的结构，利用相应的求导公式或法则就可求出.例10求下列函数的导数：解（1）y′＝e2t＋t·2e2t＝（1＋2t）e2t.（2）由于故例11设求F′（x）.解当x≠1时，F（x）在相应的定义区间上都是初等函
由于初等函数是由基本初等函数经过有限次四则运算及有限次函数复合而构成的用一个解析式表示的函数，因此结合前面的求导法则与求导公式可推得：初等函数在其定义区间上处处可导，其导函数只要按照函数的结构，利用相应的求导公式或法则就可求出.
例10 求下列函数的导数：
解 （1）y′＝e2t＋t·2e2t＝（1＋2t）e2t.
（2）由于
故
例11 设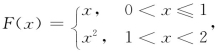
求F′（x）.
解 当x≠1时，F（x）在相应的定义区间上都是初等函数，故利用求导公式可得
由于x＝1是函数f（x）的分界点，且f（x）在x＝1的两侧的表达式不同，所以要利用该点的左、右导数的定义，求得
故F′（1）不存在.
综上
例12 设f（x）为可导函数，求函数y＝f2（sinx）的导数.(https://www.chuimin.cn)
解 由复合函数的求导法则可得
例13 设函数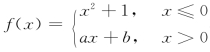
在点x＝0处连续且可导，求a，b的值.
解 由于x＝0是函数f（x）的分界点，且f（x）在x＝0的两侧的表达式不同，所以要利用定义求该点的左、右极限与导数，再考察其连续性与可导性，先考虑f（x）在x＝0处的连续性，由
得
1＝b
再考虑f（x）在x＝0处的可导性，由
得
0＝a
解得a＝0，b＝1.
相关文章
- 详细阅读
- 详细阅读
-
计算二元复合函数的偏导数与二阶偏导数详细阅读
【主要内容】设二元函数u=u（x，y），v=v（x，y）在点（x，y）处偏导数存在，函数z=f（u，v）在对应点（u，v）处可微，则复合函数z=f（u（x，y），v（x，y））在点（x，y）处的偏导数存在，且二元以上复合函数的偏导数也有类似的计算公式.注 在计算二元或二元以上复合函数的偏导数时，应先画出复合函数的关系图，然后按此图用复合函数求偏导数公式计算.例如，二元复合函数z=f（u（x，y），......
2025-09-30
-
《导数的几何意义及其应用》详细阅读
【主要内容】设函数f（x）在点x0处可导，则f′（x0）是曲线y=f（x）在点（x0，y0）（y0=f（x0））处切线的斜率.曲线y=f（x）在点（x0，y0）处的切线方程为y-y0=f′（x0）（x-x0）.当f′（x0）≠0时，曲线y=f（x）在点（x0，y0）处的法线方程为注 （ⅰ）如果f′（x0）=∞，则曲线y=f（x）在点（x0，y0）处的切线方程为x=x0；如果f′（x0）=0，则曲线......
2025-09-30
-
南高而村：抗日模范村详细阅读
在上级党组织和村支部的领导下，党员同志充分发挥模范带头作用，积极分子纷纷响应，南高而村中各种形式的抗日活动搞得轰轰烈烈，热火朝天。1942年4月又成立了南高而儿童剧团，成员多数是学生。抗战期间，南高而这个当时仅有200余户的山村，就有300多人参加了八路军和县大队等抗日武装；20多名同志以身殉国。故此他们又亲切地称南高而村是“革命摇篮”，而当地的群众则称赞南高而村为“小延安”。......
2025-09-30
-
复变函数应用：高阶导数公式详细阅读
解析函数不仅有一阶导数,而且有各高阶导数,它的值也可以用函数在边界上的值通过积分来表示.但是对于一元实函数来说,它在某一区间上可导,其导数在这区域上是否连续也不一定,更不要说它有高阶导数存在了.关于解析函数的高阶导数我们有下面的定理.定理2 解析函数f(z)的导数仍为解析函数,它的n阶导数为其中C为在函数f(z)的解析区域D内围绕z0 的任何一条正向简单闭曲线,而且它的内部全含于D.证明 设z0为......
2025-09-30
-
高含沙水流的运动方式和特点详细阅读
考虑流态的不同和水流类型的差异，高含沙水流一般存在伪一相流 、高含沙紊流型两相流、层移质运动和粘性泥石流等不同运动形式。粘性泥石流为非牛顿体流动，其显著特征是发生“铺床”现象和间歇性的阵流。......
2025-09-29
- 详细阅读
相关推荐