首页理论教育高数上册：反函数、复合函数求导法则

高数上册：反函数、复合函数求导法则

2023-11-19 理论教育版权反馈

【摘要】：1）反函数的求导法则求导法则Ⅱ设y＝f（x）在区间Ix内单调、可导，且f′（x）≠0，则其函数x＝φ（y）在相应的区间Iy内也单调、可导，且证设函数的y＝f（x）的反函数x＝φ（y）的自变量y的增量为Δy，则相应地x的增量为Δx.由函数可导必连续的性质及反函数的连续性可得，x＝φ（y）在区间Iy内单调、连续，因此当Δy→0时，有Δx→0.且当Δy≠0时，有Δx≠0，则y，y＋Δy∈Iy，设Δy

1）反函数的求导法则

求导法则Ⅱ　设y＝f（x）在区间Ix内单调、可导，且f′（x）≠0，则其函数x＝φ（y）在相应的区间Iy内也单调、可导，且

证　设函数的y＝f（x）的反函数x＝φ（y）的自变量y的增量为Δy，则相应地x的增量为Δx.由函数可导必连续的性质及反函数的连续性可得，x＝φ（y）在区间Iy内单调、连续，因此当Δy→0时，有Δx→0.且当Δy≠0时，有Δx≠0，则∀y，y＋Δy∈Iy，设Δy≠0，有

证毕.

例8　求反正弦函数y＝arcsinx（｜x｜＜1）的导数.

解　由于x＝siny在区间内单调、可导，且其导数cosy≠0.因此，其反函数y＝arcsinx在相应的区间（－1，1）内单调、可导，且由反函数求导公式得

即

同理可得

2）复合函数的求导法则

很多情况下还会遇到复合函数的求导问题，下面推导复合函数的求导公式.

求导法则Ⅲ　设函数u＝φ（x）在x处可导，函数y＝f（u）在相应的点u处可导，则复合函数y＝f［φ（x）］在x处也可导，且

或

证　设x有增量Δx，则相应地u有增量Δu，复合函数y有增量Δy.

由u＝φ（x）在x处可导则必连续可知，当Δx→0时，有Δu→0.

当Δu≠0时，则(www.chuimin.cn)

当Δu＝0时，则相应地Δy＝0，则必有也成立.

因此复合函数y＝f［φ（x）］在x处的求导法则为

（f［φ（x）］）′＝f′［φ（x）］·φ′（x）

上式中（f［φ（x）］）′表示复合后的函数y＝f［φ（x）］对自变量x的导数，f′［φ（x）］表示函数f（u）对u的导数.

该求导法则可以推广到有限个函数复合的情形.

推论3　设函数y＝f（u），u＝φ（v），v＝ψ（x）复合成函数y＝f｛φ［ψ（x）］｝，若f（u），φ（v），ψ（x）均可导，则复合函数f｛φ［ψ（x）］｝也可导，且有

或

上式右端的求导法则，按y→u→v→x的顺序，就像一条链子一样，因此通常将复合函数的求导法则Ⅲ及推论3称为链式法则.

例9　求函数y＝ln｜x｜的导数.

解　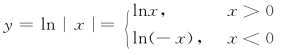　 pagenumber_ebook=95,pagenumber_book=84

当x＞0时

当x＜0时

因此

上式也是一个常用的公式，必须熟记.