高等数学上册：导数概念

2023-11-19 理论教育版权反馈

【摘要】：1）几个实际问题（1）平面曲线的切线问题设点M0（x0，y0）与M（x，y）分别是平面曲线y＝f（x）上的一个定点与动点，则割线MM0的斜率为根据切线的定义可知，当M→M0，即Δx→0时，若存在，则该极限就等于切线的斜率，即因此曲线y＝f（x）在点M0（x0，y0）处的切线方程为y－y0＝k（x－x0）（2）变速直线运动的瞬时速度问题设质点M沿某直线作s＝s（t）的变速直线运动，s（t）为t时刻质

1）几个实际问题

（1）平面曲线的切线问题

设点M0（x0，y0）与M（x，y）分别是平面曲线y＝f（x）上的一个定点与动点，则割线MM0的斜率为

根据切线的定义可知，当M→M0，即Δx→0时，若存在，则该极限就等于切线的斜率，即

因此曲线y＝f（x）在点M0（x0，y0）处的切线方程为

y－y0＝k（x－x0）

（2）变速直线运动的瞬时速度问题

设质点M沿某直线作s＝s（t）的变速直线运动，s（t）为t时刻质点M所经过的路程，在时间段［t0，t］内，质点运动的平均速度为

Δt越小， pagenumber_ebook=83,pagenumber_book=72 （t）就越接近t0时刻的瞬时速度v（t0），所以平均速度的极限就是t0时刻的瞬时速度v（t0），即

（3）边际成本问题

设C＝f（x）表示产品生产或销售的某种成本函数，x为产品数量，若生产或销售的产品数量从x0增加到x0＋Δx，则相应增加的成本为ΔC＝f（x0＋Δx）－f（x0）.因此表示产品数量从x0增加到x0＋Δx时的成本提高的平均速度，Δx越小，则就越接近x0时刻生产或销售成本提高的瞬时速度，因此

表示产品数量为x0时，生产或销售成本提高的瞬时速度.其意义即在生产或销售的产品数量为x0时，每增加1个产品所需增加的成本，这在经济学中称为边际成本.

2）导数的定义

从以上几个实际问题中可以看出，三类问题的实际意义虽各不相同，但摆脱所有的实际含义后，其数量关系相同，本质上都是求已知函数在一点处的函数增量与自变量增量的比值的极限，此极限表示函数在该点处的瞬时变化率，我们称之为导数.

在自然科学与工程技术领域中，还有许多关于瞬时变化率的问题，从这些问题中抽象出它们在数量关系上的共性，得到导数的定义.

定义1　设函数y＝f（x）在x0的某个邻域内有定义，当自变量在这个邻域内从x0变到x0＋Δx（Δx≠0）时，相应地函数有增量Δy＝f（x0＋Δx）－f（x0），如果极限存在，则称函数y＝f（x）在点x0处可导，并称此极限为函数f（x）在x0处的导数，记作

在定义1中，若记x＝x0＋Δx，则（2－1）式可写成

当式（2－1）或（2－2）中的极限不存在时，则称函数f（x）在x0处不可导.

若函数f（x）在x0处不可导的原因是为了方便起见，也说f（x）在x0处的导数为无穷大，记作f′（x0）＝∞.

由导数定义可知，前面三个实际问题的结果可表示为：

①曲线y＝f（x）在点（x0，f（x0））处的切线的斜率为k＝f′（x0）；

②变速直线运动s＝s（t）在时刻t0处的瞬时速度为v（t0）＝s′（t0）；

③生产或销售成本函数为C＝f（x）时，在生产或销售的产品数为x0时的边际成本为f′（x0）.

下面利用导数定义讨论一些简单函数的导数或可导性.

例1　设f（x）＝x3，证明：∀x0∈R，有

证　∀x0∈R，

所以

即

例2　讨论函数在x＝0处的可导性.

解　在x＝0处，由于

所以

即该函数在x＝0处不可导.

下面利用函数左、右极限的定义，得出相应函数的左、右导数的定义.

定义2　如果右极限

存在，则称此右极限为函数y＝f（x）在x0处的右导数，记作f′＋（x0），即

类似地，如果左极限

存在，则称此左极限为函数y＝f（x）在x0处的左导数，记作f′－（x0），即

由极限存在的充要条件可知函数y＝f（x）在x0处可导的充要条件为f（x）在x0处的左、右导数存在且相等.

常利用上述充要条件讨论分段函数在分段点处的可导性.

例3　设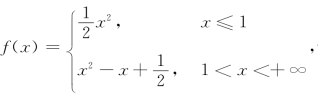 pagenumber_ebook=85,pagenumber_book=74 讨论f（x）在x＝1处的可导性，若可导，求f′（1）.

解　在x＝1处由

即f′＋（1）＝f′－（1）＝1，故f（x）在x＝1处可导，且f′（1）＝1.

例4　讨论函数f（x）＝｜x｜在x＝0处的可导性.

解　由(www.chuimin.cn)

即

f′＋（0）≠f′－（0）

故f（x）在x＝0处不可导.

利用函数的导数定义也可以解决一类特殊的函数极限问题.

例5　设f（x）在x0处可导，求

解　由题设可知

令Δx＝－h，则

所以

下面给出函数在区间上可导的定义.

定义3　（1）如果函数f（x）在开区间（a，b）内每一点处都可导，则称f（x）在（a，b）内可导.

（2）如果f（x）在（a，b）内可导，且f′＋（a）与f′－（b）均存在，则称f（x）在闭区间［a，b］上可导.

设函数f（x）在区间I内可导，则对I内的每一点x，都有一个确定的值f′（x）与之对应，由此构成了一个新的函数f′（x），称这个新函数为函数f（x）在集合I内的导函数（简称导数），记作

将式（2－1）中的x0换成x，便可得导函数的表达式：

必须指出，上式中Δx是求极限时的变量，x为求该极限时的常数.

由式（2－1）与（2－3）可知，函数f（x）在x0处的导数f′（x0）就是导函数f′（x）在x＝x0处的函数值，即

特别指出的是［f（x0）］′＝0，不能将f′（x0）与［f（x0）］′相混淆.

一般地，求函数y＝f（x）的导数步骤为：

①求函数的增量Δy＝f（x＋Δx）－f（x）；

②求增量比

③求增量比的极限

若该极限存在，则函数y＝f（x）在x处可导，且若该极限不存在，则函数y＝f（x）在x处不可导.

例6　求f（x）＝C（C为常数）的导数.

解　∀x∈R，由于

故

例7　求幂函数y＝xμ（μ为常数）的导数.

解　设y＝xμ的定义域为D，∀x∈D，由于

故

特别地，

（xn）′＝nxn－1　（n为整数）

式（2－5）称为幂函数的求导公式，利用其可直接求幂函数的导数，例如：

例8　求y＝cosx的导数，并求.

解　∀x∈R，由

则

即

因此

同理可证：

例9　求对数函数y＝lnx的导数.

解　∀x＞0，由于

故

例10　求指数函数y＝ax（a＞0，a≠1）的导数.

解　∀x∈R，由于

故

特殊地，取a＝e，有

高等数学上册：导数概念

相关推荐