高等数学上册:零点存在定理与介值定理

2025-09-30 理论教育版权反馈

【摘要】：，xn是（a，b）内任意n个点，证明：ξ∈［a，b］，使得证因为f在［a，b］上连续，且f≥0，故f在［a，b］上存在最大值M与最小值m，且M，m均大于或等于0，则由介值定理的推论可知，ξ∈［a，b］，使得

若x0满足f（x0）＝0，则称x0为函数f（x）的一个零点.

定理3（零点存在定理）　设函数f（x）在闭区间［a，b］上连续，如果f（x）在区间两端点处的值异号，则必在区间（a，b）内取得零值.

证明略.

零点存在定理的意思是：若f（x）在闭区间［a，b］上连续，且f（a）与f（b）异号（即f（a）·f（b）＜0），则至少存在一点ξ∈（a，b），使

f（ξ）＝0

在几何上，定理3表明，如果连续曲线y＝f（x）的两个端点分别位于x轴的上、下两侧，则这段曲线与x轴至少有一个交点（图1－29）.

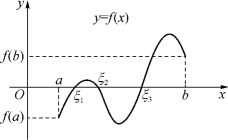
pagenumber_ebook=79,pagenumber_book=68

图1－29

在代数上，如果f（x）在闭区间［a，b］上连续，且f（a）·f（b）＜0，则方程f（x）＝0在开区间（a，b）内至少有一个根.

利用这一定理可研究方程f（x）＝0的根的范围.

例1　证明方程sinx－x＋1＝0在（0，π）内至少有一个实根.

解　设f（x）＝sinx－x＋1，显然f（x）在［0，π］上连续，又由于

f（0）＝1＞0，f（π）＝sinπ－π＋1＝1－π＜0

由零点存在定理可知，f（x）在（0，π）内至少有一个零点，即方程sinx－x＋1＝0在（0，π）内至少有一个实根.

定理4（介值定理）　设函数f（x）在闭区间［a，b］上连续，且f（a）≠f（b），则f（x）必能取得介于该区间端点处的两个数值f（a），f（b）之间的任何值.

介值定理的意思是：若f（x）在这区间的两端点处取不同的函数值f（a）＝A及f（b）＝B，则对于介于A与B之间的任意一个实数C，在（a，b）内至少存在一点φ，使得f（φ）＝C.(https://www.chuimin.cn)

证　令F（x）＝f（x）－C，则F（x）在［a，b］上连续.设f（a）＝A，f（b）＝B，因为C介于A，B之间，不妨设A＜B，则

A＜C＜B

故

F（a）＝A－C＜0，F（b）＝B－C＞0

由零点存在定理可知，∃ξ∈（a，b），使得F（ξ）＝0，即

f（ξ）＝C

推论　在闭区间上连续的函数必取得介于最大值与最小值之间的任何值.

该推论由读者自证.

例2　设非负函数f（x）在区间［a，b］上连续，x1，x2，…，xn是（a，b）内任意n个点，证明：∃ξ∈［a，b］，使得

证　因为f（x）在［a，b］上连续，且f（x）≥0，故f（x）在［a，b］上存在最大值M与最小值m，且M，m均大于或等于0，则

由介值定理的推论可知，∃ξ∈［a，b］，使得