，xn是（a，b）内任意n个点，证明：ξ∈［a，b］，使得证因为f在［a，b］上连续，且f≥0，故f在［a，b］上存在最大值M与最小值m，且M，m均大于或等于0，则由介值定理的推论可知，ξ∈［a，b］，使得......
2023-11-19
高等数学上册：最大值与最小值存在定理
【摘要】：1）最大（小）值的概念定义1设函数f（x）在区间I上有定义，若x0∈I，对x∈I都有f（x）≤f（x0）（或f（x）≥f（x0））则称f（x0）为函数f（x）在I上的最大值（或最小值），记作例如，y＝1－sinx，在闭区间［0，2π］上有而y＝x2在开区间（a，b）（b＞a＞0）内既无最大值又无最小值.2）最大（小）值存在定理定理1在闭区间上连续的函数必在该区间上取得最大值与最小值.证明略.
1）最大（小）值的概念
定义1 设函数f（x）在区间I上有定义，若∃x0∈I，对∀x∈I都有
f（x）≤f（x0） （或f（x）≥f（x0））
则称f（x0）为函数f（x）在I上的最大值（或最小值），记作
例如，y＝1－sinx，在闭区间［0，2π］上有
而y＝x2在开区间（a，b）（b＞a＞0）内既无最大值又无最小值.
2）最大（小）值存在定理
定理1 在闭区间上连续的函数必在该区间上取得最大值与最小值.
证明略.
定理1是指，如果函数f（x）在闭区间［a，b］上连续，则在［a，b］上至少存在两点x1和x2，使得对∀x∈［a，b］，恒有
f（x1）≤f（x）≤f（x2）(www.chuimin.cn)
即f（x1）与f（x2）分别是f（x）在［a，b］上的最小值与最大值（图1－27）.这样的点x1，x2在［a，b］上一定存在，有可能在（a，b）内，也有可能是闭区间的端点.
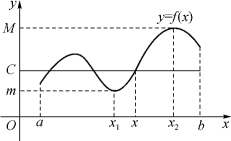
图1－27
必须注意该性质在开区间内不一定成立.例如定义在区间
内的连续函数y＝tanx在
内就取不到最大值与最小值，而在
上的连续函数y＝tanx就有最大值
与最小值
.
另外还要注意，若函数在闭区间上有间断点时，也不一定有此性质.例如，
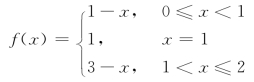
显然f（x）在闭区间［0，2］上有定义，但
因此x＝1为f（x）的间断点，事实上，f（x）在闭区间［0，2］上不存在最大值与最小值（如图1－28所示）.
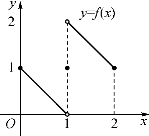
图1－28
由定理1显然可得到下面的有界性定理.
有关高等数学 上册的文章
- 详细阅读
-
高等数学上册：泰勒中值定理详细阅读
＝1）所以例4求f＝sinx的麦克劳林展开式.解在x∈时，即所以当取k＝0时，得sinx的一次近似式为sinx≈x此时误差为当取k＝1时，得sinx的三次近似式为此时误差为当取k＝2时，得sinx的五次近似式为此时误差为图3－3是sinx及以上三个近似多项式的图形，读者可以进行比较.图3－3类似地，还可得到其中......
2023-11-19
-
拉格朗日中值定理-高等数学 上册详细阅读
取消罗尔定理中关于“函数在两端点处的函数值必须相等”的条件，就可得到一般情形下的微分中值定理，也称为拉格朗日中值定理.定理3（拉格朗日中值定理）若y＝f（x）在［a，b］上连续，在（a，b）内可导，则ξ∈（a，b），使得证设辅助函数则定理2的结论可写成下面验证函数F（x）在［a，b］上满足罗尔定理的三个条件.由于f（x）在［a，b］上连续，在（a，b）内可导，故F（x）在［a，b］上连续，在（......
2023-11-19
-
高数上册-函数最大最小值详细阅读
解设圆柱形密闭锅炉的底半径为R，高为h，则其表面积S＝2πRh＋2πR2由将它代入上式得由解得唯一的驻点又由于制造固定容积的圆柱形密闭锅炉时，一定存在一个底半径，使锅炉的表面积最小.因此，当时，S在该点取得最小值.此时，相应的高即当圆柱形密闭锅炉的高与底直径都等于时，表面积最小，从而使用料最省.......
2023-11-19
-
高等数学上册：原函数的存在性及唯一性问题详细阅读
定义1设函数f是定义在区间I上的已知函数，若存在函数F，满足对x∈I，恒有F′＝f则称函数F为f在区间I上的一个原函数.例如，因是x4在R上的一个原函数.又如，arctanx－1与arctanx＋2都是在R上的原函数，容易看出arctanx＋C都是的原函数.可见，研究原函数首先要解决下面两个主要问题.满足何种条件的函数必定存在原函数？如果已知某个函数的原函数存在，那么原函数是否唯一？如果不唯一，原函数之间有什么关系？......
2023-11-19
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2023-11-19
-
数列极限：高等数学上册详细阅读
对于给定的数列｛xn｝，我们讨论当项数n无限增大时（记作n→∞），对应项的变化趋势.观察上面的四个数列，容易看出，当n→∞时，数列趋于1；数列各项的值在数1的两侧来回交替着变化，且越来越接近1；数列｛2n－1｝越来越大，无限增大；数列｛1－（－1）n｝各项的值永远在0与2之间交互取得，而不与某一数接近.如果当n→∞时，数列的项xn能无限接近于某个常数A，则称这个数列为收敛数列，常数A称为当n→∞时......
2023-11-19
-
高等数学上册：函数极值详细阅读
定义1凡是满足方程f′（x）＝0的点x称为函数f（x）的驻点.根据导数的几何意义，在曲线y＝f（x）上驻点处的切线是水平的.图3－9在图3－9中，考察函数f（x）在［a，b］上的极值与最值，发现：函数f（x）在点x1，x2，x3处取得极大值，函数f（x）在x′1，x′2，x′3处取得极小值；其最大值为f（b），最小值为f（x′2）.观察该图还发现：函数在一个区间内可以有若干个极大值与极小值，函数......
2023-11-19
相关推荐