初等函数连续性-高数上册

2025-09-30 理论教育版权反馈

【摘要】：）时无意义，故x＝kπ（k＝0，±1，±2，…）均为的间断点.当x＝0时，由于故x＝0为f的第一类可去型间断点；当x＝kπ（k＝±1，±2，…）为f的第二类无穷型间断点.

1）基本初等函数的连续性

我们知道三角函数与反三角函数均在相应的区间上连续，下面讨论指数函数、对数函数及幂函数的连续性.

例9　证明：指数函数y＝ax（a＞0，a≠1）在其定义域内处处连续.

证　∀x0∈R，有

故

即指数函数y＝ax在其定义域R内处处连续.

由反函数的连续性可知，指数函数的反函数y＝logax在其定义域（0，＋∞）内也连续.

由于xa＝ealnx，再由复合函数的连续性可知幂函数y＝xa在其定义域内也是连续的.

综上所述，可知五类基本初等函数在它们的定义区间上都是连续的.再根据连续函数的四则运算及复合运算法则可得如下重要结论：

一切初等函数在其定义区间上处处连续.

利用这一结论，对已知连续性的函数，求极限就变得很简单：若f（x）在x0处连续，则

特别地，当f（x）为初等函数，而x0是f（x）在其定义区间内的点时，有

例10　求下列极限：

解　（1）由于函数lntanx在处连续，所以(https://www.chuimin.cn)

（2）由于函数故该函数在x＝2处连续，所以

例11　设函数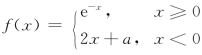 pagenumber_ebook=76,pagenumber_book=65 在x＝0处连续，求a的值.

解　由f（0）＝e0＝1，且

根据f（x）在x＝0处连续，得

解得，a＝1时，f（x）在x＝0处连续.

例12　求函数的间断点，并判别其类型.

解　由sinx＝0，解得

x＝kπ　（k＝0，±1，±2，…）

当x＝kπ（k＝0，±1，±2，…）时无意义，故x＝kπ（k＝0，±1，±2，…）均为的间断点.

当x＝0时，由于

故x＝0为f（x）的第一类可去型间断点；

当x＝kπ（k＝±1，±2，…）时，由于

故x＝kπ（k＝±1，±2，…）为f（x）的第二类无穷型间断点.