定义3 设二元函数f(x,y)在开区域(或闭区域)D内有定义,P0(x0,y0)是D内的点(或边界点且P0∈D),如果则称函数f(x,y)在点P0(x0,y0)连续.如果函数f(x,y)在开区域(或闭区域)D内的每一点连续,那么就称函数f(x,y)在D内连续,或者称f(x,y)是D内的连续函数.若函数f(x,y)在点P0(x0,y0)处不连续,则称P0为函数f(x,y)的间断点.前面已经讨论过的函......
2023-10-19
我们观察到许多曲线的图形在一定的范围内是连续不间断的,其直观的概念是能够在笔不提起的情况下一笔画出一个函数的图形.自然界中的许多现象如空气、水的流动,气温高低变化等也都是连续变化着的.在数学上,称这些现象具有连续性.下面讨论一元函数的连续性.
为了准确地用数学语言描述函数的这种性态,先介绍增量(改变量)的概念.
1)增量
若变量u从始点u1变化到终点u2,则称u2-u1为变量u的增量(或改变量),记作Δu,即
Δu=u2-u1 (或u2=u1+Δu)
当u的值变大、变小或不变时,对应的Δu分别为正数、负数、0(图1-24).
![]()
图1-24
设函数y=f(x)在U(x0)内有意义,自变量x的始点为x0,并在x0处有增量Δx,则x从x0变到了x0+Δx,相应地,函数y从f(x0)变到了f(x0+Δx),这时函数的增量为
Δy=f(x0+Δx)-f(x0)
2)函数在点x0处的连续性
容易观察到,如果曲线y=f(x)在定义域内的点x0处的图形没有断开,这时f(x)在x0处就有一个共同的特点:当自变量的改变量无限小时,相应函数值的改变量也无限小.例如关于细金属丝的长度,当温度T的增量ΔT很微小时,其相应的长度l的增量Δl也很微小,而且|Δl|可以小于预先任意指定的程度,只要|ΔT|充分小.即当ΔT→0时,Δl→0,我们将具有这种特性的点x0称为函数的连续点.
根据以上分析,给出函数在一点连续的定义如下.
定义1 设f(x)在点x0的某邻域U(x0)内有定义,若当自变量x的增量Δx=x-x0趋向于零时,对应函数的增量Δy=f(x0+Δx)-f(x0)也趋向于零,即
![]()
则称函数y=f(x)在点x0处连续.
由于
Δx=x-x0,Δy=f(x)-f(x0)
则
![]()
故定义1与下面的的定义等价.
定义1′ 设f(x)在点x0的某邻域U(x0)内有定义,若f(x)在点x0处满足(www.chuimin.cn)
![]()
则称函数y=f(x)在点x0处连续.
由以上定义可知,函数f(x)在点x0处连续必须同时满足下列三个条件:
①y=f(x)在U(x0,δ)内有定义;
②极限![]() 存在;
存在;
③![]()
根据左、右极限的定义,得到函数左、右连续的定义.
定义2 设函数y=f(x)在区间(x0-δ,x0]上有定义,若有![]() f(x0),则称f(x)在点x0处左连续;设函数y=f(x)在区间[x0,x0+δ)上有定义,若有
f(x0),则称f(x)在点x0处左连续;设函数y=f(x)在区间[x0,x0+δ)上有定义,若有![]() 则称f(x)在点x0处右连续.
则称f(x)在点x0处右连续.
由极限存在的充要条件可知:函数f(x)在点x0处连续的充要条件为f(x)在点x0处右连续且左连续.
例1 设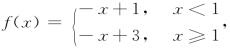 讨论f(x)在点x=1处的连续性.
讨论f(x)在点x=1处的连续性.
解 由于f(1)=2,而
![]()
故f(x)在点x=1处右连续但不左连续,故f(x)在点x=1处不连续.
3)函数在区间上的连续性
定义3 若函数y=f(x)在区间上每一点都连续,则称函数y=f(x)在该区间上连续.如果区间包括端点,那么函数在右端点处的连续是指左连续,在左端点处的连续是指右连续.
若函数f(x)在其定义域上的每一点处都连续,则称f(x)为定义域上的连续函数,简称连续函数.
例如对于多项式函数pn(x)=anxn+an-1xn-1+…+a0,由于![]() pn(x0)(∀x0∈R),故多项式函数在R内连续.
pn(x0)(∀x0∈R),故多项式函数在R内连续.
又如三角函数y=sinx,y=cosx,由于
![]()
故它们也均在R内连续.
在几何上,连续函数的图形是一条连绵不断的曲线.
有关高等数学 上册的文章

定义3 设二元函数f(x,y)在开区域(或闭区域)D内有定义,P0(x0,y0)是D内的点(或边界点且P0∈D),如果则称函数f(x,y)在点P0(x0,y0)连续.如果函数f(x,y)在开区域(或闭区域)D内的每一点连续,那么就称函数f(x,y)在D内连续,或者称f(x,y)是D内的连续函数.若函数f(x,y)在点P0(x0,y0)处不连续,则称P0为函数f(x,y)的间断点.前面已经讨论过的函......
2023-10-19

一、连续函数的概念在自然界中有许多现象都是连续不断地变化的,如,气温随着时间的变化而连续变化;金属轴的长度随气温有极微小的改变也是连续变化的等.这些现象反映在数量关系上就是我们所说的连续性.函数的连续性反映在几何上可以看作一条不间断的曲线;下面给出连续函数的概念.(一)函数的增量增量的定义,简单说,就是变化后的量减去变化前的量.例如:早晨t1=8时,温度T1=2℃,中午t2=14时,温度T2=12......
2023-11-20

解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30

解 由于f=1,且因此函数f在点x0=0处右连续但不左连续,所以函数f在x0=0处不连续.例4 设函数讨论f在x=1处的连续性.解 由于f=2,且因此函数f在x=1处左连续且右连续,所以函数f在x=1处连续.例5 设函数问:a为何值时,函数y=f在点x=0处连续?......
2023-11-20

)时无意义,故x=kπ(k=0,±1,±2,…)均为的间断点.当x=0时,由于故x=0为f的第一类可去型间断点;当x=kπ(k=±1,±2,…)为f的第二类无穷型间断点.......
2023-11-19

一、函数的单调性从图上可以直观地看出,单调增加函数的切线斜率非负(见图3-3),单调减少函数的切线斜率非正(见图3-4).图3-3图3-4定理3.7 设函数f(x)在区间I内可导,则:1)对任意x∈I,有f′(x)>0,则函数f(x)在I严格单调增加;2)对任意x∈I,有f′(x)<0,则函数f(x)在I严格单调减少.证 先证1)对任意x1,x2∈I且x1<x2,函数f(x)在区间[x1,x2]上......
2023-11-22

复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.定义3 设函数w = f(z)在点z0的去心邻域:0 <|z - z0| <ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε >0,总存在一个实数δ >0(δ <ρ),当0 <|z-z0|<δ 时,有|f(z)-A|<ε,我们称A为f(z)当z趋于z0时的极限,记为复变函数极限的几......
2023-10-30
相关推荐