首页理论教育无穷小量比较：高等数学上册

无穷小量比较：高等数学上册

2023-11-19 理论教育版权反馈

【摘要】：我们已经知道两个无穷小量的和、差、积仍为无穷小，但两个无穷小量的商的情形就较为复杂，例如下面几个简单的无穷小量的商的极限：从上面三个极限中就看出：虽然当x→0时，x3，x2，x，1－cosx都是无穷小，但它们比值的极限却有着各自不同的情形，分析这些情形产生的原因，发现是由于各个无穷小趋于零的快慢程度不同而造成的.就上面的例子来说，在x→0的过程中，x2→0的速度比x→0要快，x2→0的速度比x3→

我们已经知道两个无穷小量的和、差、积仍为无穷小，但两个无穷小量的商的情形就较为复杂，例如下面几个简单的无穷小量的商的极限：

从上面三个极限中就看出：虽然当x→0时，x3，x2，x，1－cosx都是无穷小，但它们比值的极限却有着各自不同的情形，分析这些情形产生的原因，发现是由于各个无穷小趋于零的快慢程度不同而造成的.就上面的例子来说，在x→0的过程中，x2→0的速度比x→0要快，x2→0的速度比x3→0要慢，而1－cosx→0的速度与x2→0差不多，保持了倍数关系.事实上，两个无穷小的比较反映了两个无穷小趋于零的相对快慢程度，在高等数学中占有重要地位.下面我们利用两个无穷小的商的极限引入无穷小量阶的概念.

定义1　设α，β是同一变化过程中的两个无穷小，

（1）若则称在此变化过程中，α为β的高阶无穷小，记作α＝o（β）（x→□或n→∞）.

（2）若，则称在此变化过程中，α为β的低阶无穷小.

（3）若（c为常数且c≠0），则称在此变化过程中，α是β的同阶无穷小；特别地，当c＝1时，称在此变化过程中，α与β是等价无穷小，记作α～β（x→□或n→∞）.

（4）若，则称在此变化过程中，α为β的k阶无穷小.

一般地，当讨论无穷小α的阶数时，若极限过程为x→0，则常取β＝x；当x→∞时，则常取当x→x0时，则常取β＝x－x0.

例如，由于

因此当x→0时，sin3x是x的高阶无穷小，即sin3x＝o（x）（x→0）.

因为

所以当n→∞时的低阶无穷小.

因为所以当x→0时，1－cosx与x2是同阶无穷小.

因为所以当x→0时，sinx与x是等价无穷小，即sinx～x（x→0）.

例1　验证函数在x→0时是无穷小，并求其阶数.

解　由于

故函数在x→0时是无穷小，又

所以x→0时是关于x的一阶无穷小.

下面着重讨论等价无穷小的几个重要性质.

性质1　在某一变化过程中，α与β是等价无穷小的充分必要条件为

α＝β＋o（β）　（x→□或n→∞时）

证　下面仅以x→x0的情形为例.

必要性　设α～β（x→x0），则

即

α－β＝o（β）　（x→x0）

因此

α＝β＋o（β）　（x→x0）

充分性　设α＝β＋o（β）（x→x0），则(www.chuimin.cn)

则

α～β　（x→x0）

综上

α～β　（x→x0）⇔α＝β＋o（β）　（x→x0）

证毕.

例如，当x→0时，由于x＋x2＝x＋o（x），因此x＋x2～x（x→0）；当x→0时，由于sinx～x，因此sinx＝x＋o（x）（x→0）.

性质2　当x→0时，有如下几组常用的等价无穷小：

证　下面仅证其中三个.由于

因此，当x→0时

arctanx～x，ln（1＋x）～x，ex－1～x

其他由读者自证.

性质3　设当x→□时，α（x）～α′（x），β（x）～β′（x），f（x）为已知函数，且存在（或为∞），则

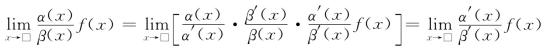
证　 pagenumber_ebook=66,pagenumber_book=55

证毕.同理可证如下类似结论：

性质3′　当x→□时，α（x）～α′（x），f（x）为已知函数，且存在（或为∞），则

证明由读者自证.

例2　计算

解　因为x→0时，sin2x～2x，tan3x～3x，所以

例3　计算

解　因为x→0时，arcsin2x～2x，x2＋2x＝2x＋o（2x）～2x，所以

例4　计算

解　因为x→0时所以

例5　计算

解　因为x→0时故

注意，利用无穷小代换时只能对函数中的乘积因子进行，对于其加减因式则不能进行无穷小代换，否则就会出错.例如对于极限如果直接进行tanx～x，sinx～x的代换，则

而由上一节的例题可知其等于，显然上面的做法是错的.事实上有