定义1称满足条件xn≤xn＋1（n＝1，2，…）即｛xn｝单调增加.下面再证｛xn｝上有界：由xn的展开式可知即｛xn｝上有界.因此该数列｛xn｝单调增加且有上界，由准则Ⅱ可知，极限存在，将该极限用字母e表示，即可证明e是一个无理数，且2＜e＜3，它的值为e＝2.718 281 828 459 045…......
2023-11-19
高等数学：夹逼准则-高等数学 上册
【摘要】：准则Ⅰ若函数f（x），g（x），h（x）在点x0的某去心邻域内满足条件：（1）g（x）≤f（x）≤h（x），（2）则存在，且等于a.证由于，因此，对ε＞0，δ1＞0，当x满足0＜｜x－x0｜＜δ1时，有｜g（x）－a｜＜ε，即又由于则对上面的ε＞0，δ2＞0，当x满足0＜｜x－x0｜＜δ2时，有｜h（x）－a｜＜ε，即取δ＝min｛δ1，δ2｝，则当x满足0＜｜x－x0｜＜δ时，（1－25）、
准则Ⅰ 若函数f（x），g（x），h（x）在点x0的某去心邻域内满足条件：
（1）g（x）≤f（x）≤h（x），
（2）
则
存在，且等于a.
证 由于
，因此，对∀ε＞0，∃δ1＞0，当x满足0＜｜x－x0｜＜δ1时，有｜g（x）－a｜＜ε，即
又由于
则对上面的ε＞0，∃δ2＞0，当x满足0＜｜x－x0｜＜δ2时，有｜h（x）－a｜＜ε，即
取δ＝min｛δ1，δ2｝，则当x满足0＜｜x－x0｜＜δ时，（1－25）、（1－26）两式同时成立，再由条件（1），有
a－ε＜g（x）≤f（x）≤h（x）＜a＋ε
即
｜f（x）－a｜＜ε
所以
这个准则也适用于自变量的其他变化过程.对于数列极限也同样成立.
例1 证明
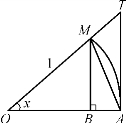
图1－23
证 在单位圆中，设∠AOM＝x，且
由于在单位圆中的弧度用x表示，则有向线段BM＝sinx，TA＝tanx，弧
（图1－23），由于
△OAM的面积＜扇形OAM的面积＜△OAT的面积
即
当
时，sinx＞0，用
除上式各项，不等式化为
又由于
因此式子
x＜0时也成立，故上式在
时成立.又已知(www.chuimin.cn)
由夹逼准则，可得
该极限在极限理论与计算中都有重要应用，所以称该极限为重要极限一.
例2 计算
解 
例3 
解
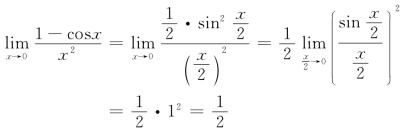
例4 计算
解
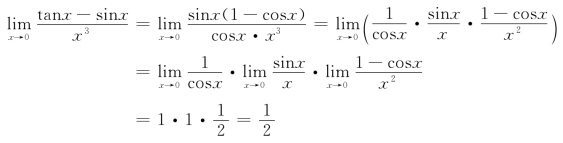
例5 计算
解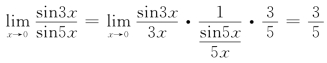 
例6 计算
解 因为
则
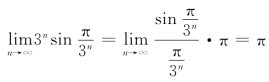
例7 求
证 因
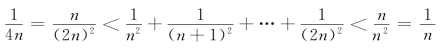
又
由夹逼准则，得
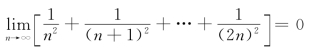
有关高等数学 上册的文章
- 详细阅读
-
高等数学上册：隐函数导数详细阅读
1）隐函数求导法（1）隐函数的导数一般地，如果方程F（x，y）＝0在一定条件下，当x在某区间内任取一值时，相应地总有满足这个方程的唯一的y值存在，那么，就称方程F（x，y）＝0在该区间上确定了一个隐函数y＝y（x）.把一个隐函数化为显函数，称为隐函数的显化.例如方程x2＋2y＝1确定的函数可显化为但有些隐函数的显化是困难的，甚至是不可能的.而在实际问题中，往往需要计算隐函数的导数，那么能否对隐函数......
2023-11-19
-
数列极限：高等数学上册详细阅读
对于给定的数列｛xn｝，我们讨论当项数n无限增大时（记作n→∞），对应项的变化趋势.观察上面的四个数列，容易看出，当n→∞时，数列趋于1；数列各项的值在数1的两侧来回交替着变化，且越来越接近1；数列｛2n－1｝越来越大，无限增大；数列｛1－（－1）n｝各项的值永远在0与2之间交互取得，而不与某一数接近.如果当n→∞时，数列的项xn能无限接近于某个常数A，则称这个数列为收敛数列，常数A称为当n→∞时......
2023-11-19
-
高等数学上册：泰勒中值定理详细阅读
＝1）所以例4求f＝sinx的麦克劳林展开式.解在x∈时，即所以当取k＝0时，得sinx的一次近似式为sinx≈x此时误差为当取k＝1时，得sinx的三次近似式为此时误差为当取k＝2时，得sinx的五次近似式为此时误差为图3－3是sinx及以上三个近似多项式的图形，读者可以进行比较.图3－3类似地，还可得到其中......
2023-11-19
-
定积分的几何意义-高等数学 上册详细阅读
若函数f（x）≥0，则在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形的面积.当函数f（x）≤0时，由定积分定义知在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形（在x轴下方）的面积的相反数.图5－3一般地，若f（x）在［a，b］上既取得正值又取得负值，则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5－3所示，有由几何意义易知，在......
2023-11-19
-
高等数学上册：函数极值详细阅读
定义1凡是满足方程f′（x）＝0的点x称为函数f（x）的驻点.根据导数的几何意义，在曲线y＝f（x）上驻点处的切线是水平的.图3－9在图3－9中，考察函数f（x）在［a，b］上的极值与最值，发现：函数f（x）在点x1，x2，x3处取得极大值，函数f（x）在x′1，x′2，x′3处取得极小值；其最大值为f（b），最小值为f（x′2）.观察该图还发现：函数在一个区间内可以有若干个极大值与极小值，函数......
2023-11-19
-
函数单调性-高等数学 上册详细阅读
函数的单调性是函数的主要性质之一，下面利用导数来研究函数的单调性的判别方法.从图3－4（a）中可看出，当沿着单调增加函数的曲线从左向右移动时，曲线逐渐上升，它的切线的倾斜角α总是锐角，即这时斜率f′（x）＞0；从图3－4（b）中可看出，当沿着单调减少函数的曲线从左向右移动时，曲线逐渐下降，其切线的倾斜角α总是钝角，即这时斜率f′（x）＜0.图3－4从上面的几何直观中可得出：当函数在区间内是单调增加......
2023-11-19
-
高等数学上册：有理函数积分详细阅读
两个多项式的商称为有理函数，其中n和m是非负整数，且a0≠0，b0≠0.当n≥m≥1时，称式（4－5）所表示的函数为有理假分式函数；当n＜m时，称式（4－5）所表示的函数为有理真分式函数.当f是假分式时，利用多项式的除法，可将它化为一个多项式与一个真分式的和.例如，因此有理函数的积分问题可归结为求真分式的积分问题.1）有理函数的分解定理1设有真分式（4－5）式，若Qm＝b0（x－a）α…（x－b）βλ…......
2023-11-19
相关推荐