利用函数极限的定义,可得下列极限的性质.1)唯一性定理2若存在,则极限唯一.证(反证法)假设极限不唯一,则存在两个不相等的常数a,b,使得均成立.不妨设b>a,由于取则δ1>0,当x满足0<|x-x0|<δ1时,恒有即又由于仍取则δ2>0,当x满足0<|x-x0|<δ2时,恒有即取δ=min{δ1,δ2},则当x满足0<|x-x0|<δ时,上面(1-5)、(1-6)两式均成立,但这是不可能的.......
2023-11-19
对于给定的数列{xn},我们讨论当项数n无限增大时(记作n→∞),对应项的变化趋势.观察上面的四个数列,容易看出,当n→∞时,
数列![]() 趋于1;
趋于1;
数列![]() 各项的值在数1的两侧来回交替着变化,且越来越接近1;
各项的值在数1的两侧来回交替着变化,且越来越接近1;
数列{2n-1}越来越大,无限增大;
数列{1-(-1)n}各项的值永远在0与2之间交互取得,而不与某一数接近.
如果当n→∞时,数列的项xn能无限接近于某个常数A,则称这个数列为收敛数列,常数A称为当n→∞时数列{xn}的极限,记作![]()
上面极限概念的表述中项xn能与某个常数A无限接近的意思可以理解为当n→∞时,|xn-A|可以任意小,即该距离可以小于任意给定的小正数,但必须以n→∞为条件,即距离|xn-A|小于任意给定的小正数的条件是要项数n足够大,大到足够保证|xn-A|小于预先任意给定的(无论怎样小的)正数.
下面我们以数列![]() 为例来讨论极限
为例来讨论极限![]() 的数学含义及精确表达.
的数学含义及精确表达.
由观察可知:当n→∞时,数列![]() 能与常数1无限接近,即
能与常数1无限接近,即![]() 的极限为1.
的极限为1.
比如对于数列![]() 若给定小正数
若给定小正数![]() ,由于
,由于![]() 可知,要使
可知,要使![]() 只要n>100就行了;又若给定小正数
只要n>100就行了;又若给定小正数 ![]() 要使
要使![]() 就需要n>10 000才行;若再给定小正数10-10,要使
就需要n>10 000才行;若再给定小正数10-10,要使![]() 就要n>1010了.尽管小正数10-10已经很小了,但是否对于无论怎样小的正数ε,不等式
就要n>1010了.尽管小正数10-10已经很小了,但是否对于无论怎样小的正数ε,不等式![]() 总能成立呢?
总能成立呢?
事实上,对于预先任意给定的无论怎样小的正数ε,要使不等式![]() <ε成立,只要
<ε成立,只要![]() 就行了.我们利用取整函数的意义,取项数
就行了.我们利用取整函数的意义,取项数![]() 则由取整函数的性质可知,当n>N时,就有
则由取整函数的性质可知,当n>N时,就有![]() 这时
这时![]() 成立.其中n>N的意思是n=N+1,N+2,N+3,…,即当项数n从第N+1项开始时,不等式
成立.其中n>N的意思是n=N+1,N+2,N+3,…,即当项数n从第N+1项开始时,不等式![]() 就成立了.
就成立了.
综上分析,利用ε-N的数量关系,可得数列极限![]() 的精确定义.
的精确定义.
定义1 设{xn}是一个数列,A是某常数,如果对∀ε>0,总存在正整数N,使得当n>N时,不等式|xn-A|<ε都成立,那么就称常数A为数列{xn}当n→∞时的极限,记作
![]()
这时我们也称数列{xn}收敛于A.如果数列{xn}没有极限,就称数列{xn}是发散的.
定义1中的正整数N与预先给定的小正数ε是有关的,它随着ε的给定而选定,一般地,当ε越小时,N将会相应地越大.
由于|xn-A|<ε⇔A-ε<xn<A+ε,所以![]() 的等价意义为:对∀ε>0,∃N,使得当n>N时,恒有A-ε<xn<A+ε成立.
的等价意义为:对∀ε>0,∃N,使得当n>N时,恒有A-ε<xn<A+ε成立.
因此对数列极限![]() 作如下的几何解释:当n→∞时,数列的项xn能与某个常数A无限接近,即随着项数n越来越大,由xn表示的点几乎全部密集在点A的ε邻域中,而在邻域外的点只有有限个(N个),将常数A及数列x1,x2,x3,…,xn,…在数轴上一一表示出来,任取一个小正数ε(无论它多么小),在数轴上作点A的ε邻域即开区间(A-ε,A+ε),则对上面的ε,必存在N,使数列中除了开始的N项外,自第N+1项起,后面所有的项
作如下的几何解释:当n→∞时,数列的项xn能与某个常数A无限接近,即随着项数n越来越大,由xn表示的点几乎全部密集在点A的ε邻域中,而在邻域外的点只有有限个(N个),将常数A及数列x1,x2,x3,…,xn,…在数轴上一一表示出来,任取一个小正数ε(无论它多么小),在数轴上作点A的ε邻域即开区间(A-ε,A+ε),则对上面的ε,必存在N,使数列中除了开始的N项外,自第N+1项起,后面所有的项
xN+1,xN+2,xN+3,…
都落在开区间(A-ε,A+ε)内(图1-18).
![]()
图1-18
例1 证明![]() .
.
证 对∀ε>0,考察
![]()
为了使|xn-A|<ε,只须![]() 成立.可取
成立.可取![]() 则当n>N时,就有
则当n>N时,就有![]() 成立,即有(www.chuimin.cn)
成立,即有(www.chuimin.cn)

即有
![]()
例2 证明![]() 这里|q|<1.
这里|q|<1.
证 ∀ε>0(不妨设ε<1),考察
|xn-A|=|qn|=|q|n<ε
在不等式两边取自然对数,得
nln|q|<lnε
由于ln|q|<0,故有
![]()
因此,要想使|xn-A|<ε成立,只要![]() 成立即可.取
成立即可.取![]() 当n>N时,有
当n>N时,有![]() 则|xn-A|<ε成立,即
则|xn-A|<ε成立,即
![]()
例3 证明![]() .
.
证 (1)当a>1时,令![]() 则h>0,且
则h>0,且
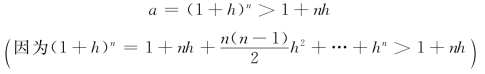
所以
![]()
对∀ε>0,要使![]() 只要
只要![]() 即只要
即只要![]() 故取N=
故取N=![]() 则
则
![]()
(2)当a=1时,显然有![]()
(3)当0<a<1时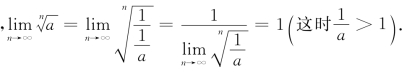
说明:上式用到的极限的运算法则将在本章1.5节中给出证明.
综上得
![]()
有关高等数学 上册的文章

利用函数极限的定义,可得下列极限的性质.1)唯一性定理2若存在,则极限唯一.证(反证法)假设极限不唯一,则存在两个不相等的常数a,b,使得均成立.不妨设b>a,由于取则δ1>0,当x满足0<|x-x0|<δ1时,恒有即又由于仍取则δ2>0,当x满足0<|x-x0|<δ2时,恒有即取δ=min{δ1,δ2},则当x满足0<|x-x0|<δ时,上面(1-5)、(1-6)两式均成立,但这是不可能的.......
2023-11-19

有,从而此时,{xn}单调减少.由以上分析可知,{xn}按和可为单调不减有上界的数列或单调减少有下界的数列,因此由数列极限存在准则Ⅱ知存在,记为A.递推式两边令n→∞取极限得, 即由于xn>0(n=1,2,…......
2023-10-27

观察函数当x趋近于∞时发现:当x趋近于∞时对应的函数值无限地与数值0接近,即当因此数值0为函数当x→∞时的极限.设a为某常数,如果当|x|无限增大时,函数f(x)与a可无限地接近,则称a是函数f(x)当x→∞时的极限,记作或f(x)→a(当x→∞时).式“x→∞”表示自变量x的绝对值无限增大的变化过程,在数轴上看,“x→∞”表示x沿着数轴向两边(或分别向右、左)移动,并离原点的距离越来越远,直至无......
2023-11-19

定理1(1)(2)(3)如果B≠0,则证(1)因为所以当x→□时,f(x)-A与g(x)-B均为无穷小,因而这两个无穷小的代数和[f(x)-A]±[g(x)-B]=[f(x)±g(x)]-[A±B]仍是当x→□时的无穷小,因此(2)由题设,可令则f(x)·g(x)=[A+α(x)]·[B+β(x)]=AB+[A·β(x)+B·α(x)+α(x)·β(x)]由无穷小的性质可知,上式中的函数A·β......
2023-11-19

极限是微积分学中一个基本概念,微分学与积分学的许多概念都是由极限引入的,并且最终由极限知识来解决.因此它在微积分学中占有非常重要的地位.我国春秋战国时期的《庄子·天下篇》中说:“一尺之棰,日取其半,万世不竭”,这就是极限的最朴素思想.一、数列极限的定义(一)数列的概念定义1按自然数顺序递增的一列数称为数列.即简记为:{un}.数列中的每一个数称为数列的项,其中第一项u1称为数列的首项,第n项称为......
2023-11-20

的极限为0.证 若q=0,结论是显然的.现设0<|q|<1,对于任意ε>0,要使得|q|n-1-0<ε,即qn-1<ε,只须在不等式两边取对数后,使得(n-1)ln|q|<lnε成立就行了.因为0<q<1,所以ln|q|<0,所以,即.取,则当n>N时,有qn-1-0<ε成立.即=0(q<1)3.数列极限的几何意义由不等式|xn-a|<ε等价于a-ε<xn<a+ε.可得到数列极限的几何意义:任意一个邻域U(a,ε),数列中总存在某一项xN,在此项后面的所有项xN+1,xN+2,…......
2023-11-22

1)隐函数求导法(1)隐函数的导数一般地,如果方程F(x,y)=0在一定条件下,当x在某区间内任取一值时,相应地总有满足这个方程的唯一的y值存在,那么,就称方程F(x,y)=0在该区间上确定了一个隐函数y=y(x).把一个隐函数化为显函数,称为隐函数的显化.例如方程x2+2y=1确定的函数可显化为但有些隐函数的显化是困难的,甚至是不可能的.而在实际问题中,往往需要计算隐函数的导数,那么能否对隐函数......
2023-11-19

定义1凡是满足方程f′(x)=0的点x称为函数f(x)的驻点.根据导数的几何意义,在曲线y=f(x)上驻点处的切线是水平的.图3-9在图3-9中,考察函数f(x)在[a,b]上的极值与最值,发现:函数f(x)在点x1,x2,x3处取得极大值,函数f(x)在x′1,x′2,x′3处取得极小值;其最大值为f(b),最小值为f(x′2).观察该图还发现:函数在一个区间内可以有若干个极大值与极小值,函数......
2023-11-19
相关推荐