高等数学：函数基本性态

2023-11-19 理论教育版权反馈

【摘要】：初等数学中已经简单介绍了函数的有界性、单调性、奇偶性、周期性，下面分别对它们作简要概括.1）有界性定义3设函数f（x）在区间I上有定义，若存在数M1，使得当x∈I时，恒有f（x）≤M1则称函数f（x）在数集I上有上界，M1为f（x）在I上的一个上界；若存在数M2，使得当x∈I时，恒有f（x）≥M2则称函数f（x）在数集I上有下界，M2为f（x）在I上的一个下界；若f（x）在数集I上既有上界，又有

初等数学中已经简单介绍了函数的有界性、单调性、奇偶性、周期性，下面分别对它们作简要概括.

1）有界性

定义3　设函数f（x）在区间I上有定义，若存在数M1，使得当∀x∈I时，恒有

f（x）≤M1

则称函数f（x）在数集I上有上界，M1为f（x）在I上的一个上界；若存在数M2，使得当∀x∈I时，恒有

f（x）≥M2

则称函数f（x）在数集I上有下界，M2为f（x）在I上的一个下界；若f（x）在数集I上既有上界，又有下界，则称f（x）在I上有界，否则就称函数f（x）在I上无界.

显然，若f（x）在I上有界，则必存在数M1，M2，使得对∀x∈I，恒有

M1≤f（x）≤M2

取M＝max｛｜M1｜，｜M2｜｝，则上式等价于

｜f（x）｜≤M

因此函数f（x）在数集I上有界的充要条件为存在正数M，使得对∀x∈I，恒有｜f（x）｜≤M.

若函数f（x）在数集I上有上界M1，在几何上表示函数y＝f（x）在数集I上的图形均位于直线y＝M1的下方；若函数f（x）在数集I上有下界M2，则表示函数f（x）在数集I上的图形均位于直线y＝M2的上方；若函数f（x）在数集I上有界，则表示必存在一个正数M，函数y＝f（x）在I上的图形位于直线y＝M与y＝－M之间.

例如，函数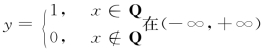 pagenumber_ebook=19,pagenumber_book=8 内有界，数1是它的一个上界，数0是它的一个下界；函数y＝x3在任一有限区间［a，b］上有界，a3与b3分别为它的一个下界与上界，但它在（－∞，＋∞）内无界.

2）单调性

定义4　设函数f（x）在区间I上有定义，如果∀x1，x2∈I，x1＜x2时，恒有f（x1）≤f（x2）（f（x1）≥f（x2）），则称函数f（x）在I上单调增加（减少）；若x1＜x2时，恒有f（x1）＜f（x2）（f（x1）＞f（x2）），则称函数f（x）在I上严格单调增加（减少）.(www.chuimin.cn)

例如，y＝x2在（－∞，0）内严格单调减少，在（0，＋∞）内严格单调增加，但在（－∞，＋∞）内不是单调函数.

又如函数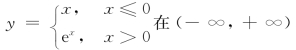 pagenumber_ebook=19,pagenumber_book=8 内单调增加，而函数y＝在任何区间上都不单调.

3）奇偶性

定义5　设函数f（x）的定义域D关于原点对称（即∀x∈D，必有－x∈D），对∀x∈D，若恒有

f（－x）＝－f（x）

则称f（x）为奇函数；若恒有

f（－x）＝f（x）

则称f（x）为偶函数.

例如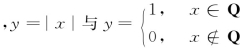 pagenumber_ebook=19,pagenumber_book=8 都是偶函数是奇函数；y＝sinx＋cosx是非奇非偶函数；y＝0既是奇函数也是偶函数.

奇函数y＝f（x）的图形关于原点中心对称（图1－5（a）），偶函数的图形关于y轴对称（图1－5（b））.

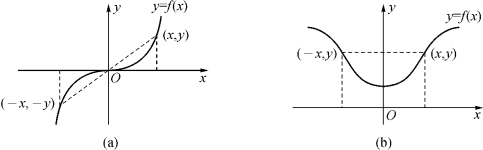
pagenumber_ebook=20,pagenumber_book=9

图1－5

4）周期性

设y＝f（x）的定义域为D，若存在非零定值T（T≠0），使得对∀x∈D，都有x＋T∈D，且等式f（x＋T）＝f（x）恒成立，则称f（x）是周期函数，T是它的一个周期.易知T的整数倍也一定是f（x）的周期.在f（x）的所有周期中，若存在最小的正数，则称这个数为f（x）的最小正周期.通常我们说周期函数的周期是指其最小正周期，例如三角函数中sinx、cosx是以2π为周期的周期函数，tanx、cotx是以π为周期的周期函数.

高等数学：函数基本性态

相关推荐