解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2025-09-30
先介绍一些数学上常用的符号.
符号“∀”表示“任意(确定)的”或者“任意一个”的意思;符号“∃”表示“存在”或者“有”的意思.例如“∀x”表示“任意(确定)的x”,而“∃x”表示“存在x”的意思.
函数研究的就是变量之间的对应关系,在同一自然现象或变化过程中,往往同时有两个或更多个变量变化着,这些变化互相联系并遵循一定的规律,函数就是描述这种联系的一个法则.例如,在初速度为0的自由落体运动中,路程s与时间t是两个变量,当时间变化时,对应的路程也随之改变,它们之间有关系
![]()
又例如在电阻两端加直流电压V,电阻中有电流I通过,电流I随电压V改变而改变,其变化规律为
![]()
若电阻R=20,则
![]()
(1-1)、(1-2)两式均表达了两个变量之间相互联系的变化规律,当取定其中一个变量的数值时,另一变量的值就随之确定,数学上把这种对应关系称为函数关系.
定义2 设同一变化过程中的两个变量为x,y,当x在给定的范围D内任意取定一个值时,另一个变量y按某一给定的法则f有一个确定的值与之相对应,就称y是x的函数,x称为自变量,y称为因变量,记作
y=f(x) (x∈D)
其中数集D称为f(x)的定义域.
一般地,在函数y=f(x)中,函数的定义域是使得式子f(x)有意义的x的集合,这时也称其为该函数的自然定义域.但在实际问题中,函数y=f(x)的定义域还要根据问题中的实际意义来确定.
由定义2可知,f(x)也表示与x对应的函数值,因此对应于x0的函数值记为![]() 全体函数值构成的集合称为函数y=f(x)的值域,记作f(D),即
全体函数值构成的集合称为函数y=f(x)的值域,记作f(D),即
f(D)={y|y=f(x),x∈D}
符号f(x)中的f表示y与x之间的对应关系,故f仅仅是一个函数对应法则的记号,也可用其他符号如φ,F等表示,这时,函数y=f(x)就可写成y=φ(x)或y=F(x).但一个函数在同一个问题中只能取定一种记号,当同一问题中涉及多个函数时,则应取不同的符号分别表示它们各自的对应法则,以免混淆.
例1 求函数![]() 的定义域.
的定义域.
解 由题意可知函数中x满足不等式组:
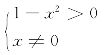
解得
-1<x<0,0<x<1 即 x∈(-1,0)∪(0,1)
则该函数的定义域为(-1,0)∪(0,1).
例2 设![]()
解 将f(x)中的变量x分别用![]() 代替,解得
代替,解得
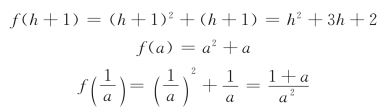
一般地,若两个函数的定义域相同,对应法则也相同,则称这两个函数相等.因此函数的定义域及其对应法则称为函数的二要素.
例如函数f(x)=lnx2与f(x)=2lnx,它们的对应法则虽相同,但定义域不同,所以它们不是相同的函数.又如函数y=x(当x≥0时)与![]() 它们的对应法则相同,定义域也相同,因此它们是相同的函数.
它们的对应法则相同,定义域也相同,因此它们是相同的函数.
一般地,如果函数y=f(x)的自变量x在定义域内任取一值时,对应的函数值y都是唯一的,则称y为x的单值函数.如果自变量x都有两个或两个以上的值y与之相对应,则称y为x的多值函数.本书中凡是没有特别说明的函数都是指单值函数.若遇到多值函数时,我们就把它化为若干个单值函数分别来讨论就可以了.
由于函数对应法则是多种多样的,因而函数的表示方法有多种形式,常见的主要有:表格法、图示法、解析(公式)法.
表格法就是把自变量x与因变量y的一些对应值用表格列出,实际应用中常用此法.例如火车时刻表就是用列表的方法列出出站和进站对应的车次与时间的函数关系.其优点是从表上可直接看出y随x的变化而变化的情况,使用上较方便,缺点是只能表达有限个对应数据.
图示法是把变量x与y对应的有序数组(x,y)看作直角坐标平面内点的坐标,y与x的函数关系就可用坐标平面内的曲线来表示.例如气象站中的温度记录器,它记录了空气中温度与时间的函数关系.这种关系是通过仪器自动描绘在纸带上的一条连续不断的曲线来表达的.其优点是直观性强,缺点是没有给出函数关系的表达式,不便于作理论上的推导与演算.(https://www.chuimin.cn)
解析法(也称公式法)是把两个变量之间的关系直接用公式或解析式表示,高等数学中所涉及的函数大多用解析法来表示.例如n次多项式函数
y=a0+a1x+a2x2+…+anxn
这里ai(i=0,1,2,…,n)均为常数,n为自然数,x为自变量,x∈R.以及有理函数
![]()
这里P(x)与Q(x)均为多项式函数,它们都是用解析式表示的函数.
有时在函数定义域的不同范围内的x所对应的函数关系并不相同,这时就要用几个不同的解析式来表示一个函数,例如函数(图1-2(a))
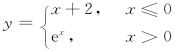
与符号函数(图1-2(b))
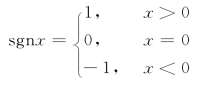
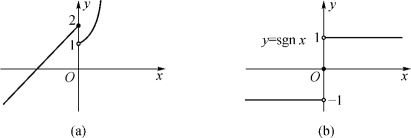
图1-2
在不同的范围内用不同的解析式分段表示的函数称为分段函数.上面两个例子就是分段函数,在自然科学与工程技术中也经常用到分段函数.
应当指出,分段函数是用不同的解析式表示一个(而不是几个)函数.因此对分段函数求函数值时,要注意自变量所在的范围,自变量在哪个范围就应代入相应范围对应的解析式中去求.
例如常用记号[x]表示“小于或等于x的最大整数”,显然[x]是由x唯一确定的,如
[-1.5]=-2,[1.3]=1,[2.43]=2,[0]=0
函数y=[x]的定义域是实数集R,值域是整数集Z,它表示y是不超过x的最大的整数.故称函数y=[x]为取整函数.该函数是分段函数,其图形如图1-3所示.
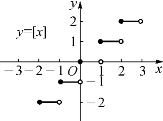
图1-3
上述用解析式或公式所表示的函数,都是直接用一个或几个关于自变量的式子来表示的,这样的函数也称为显函数.除此以外,在很多实际问题中,变量之间的函数关系也可用一个方程来表示,例如在直线方程x+2y=1中,给定实数x,就有一个确定的y值![]() 与之相对应,因此在方程x+2y=1中隐含了一个函数关系
与之相对应,因此在方程x+2y=1中隐含了一个函数关系![]() 又如椭圆的方程
又如椭圆的方程![]() 确定了两个单值函数
确定了两个单值函数![]() (当y≤0时).在xOy平面上,函数
(当y≤0时).在xOy平面上,函数![]() 表示上半椭圆,函数
表示上半椭圆,函数![]() 表示下半椭圆,这两个单值函数称为原来函数的单值分支,它们都是由方程
表示下半椭圆,这两个单值函数称为原来函数的单值分支,它们都是由方程![]() 确定的.但也有一些方程确定的函数关系不那么容易甚至不可能直接用自变量的解析式表示出来.例如开普勒(Kepler)方程
确定的.但也有一些方程确定的函数关系不那么容易甚至不可能直接用自变量的解析式表示出来.例如开普勒(Kepler)方程
y-x-εsiny=0 (ε为常数,0<ε<1)
在这个方程中不可能将y用x的解析式表示出来,尽管如此,它仍能确定y是x的函数.
若能由一个二元方程F(x,y)=0确定y是x的函数(满足函数的定义),则称函数y=y(x)是由方程F(x,y)=0确定的隐函数.有时直接通过对方程恒等变形,可以将这个隐函数求出,例如由方程2x+5y=2可以解得函数![]() 这个过程称为隐函数的显化.例如方程x2+y2=a2当y≥0时可显化为函数y=
这个过程称为隐函数的显化.例如方程x2+y2=a2当y≥0时可显化为函数y=![]() 它的图形为以原点为中心、半径为a的上半圆周.但不是每个隐函数都可以显化,如方程exy+x-siny=1确定的隐函数是无法显化的,因此隐函数是表达函数的一种必不可少的形式.需要注意的是:任意一个方程并不一定就能确定一个隐函数.究竟在什么条件下能够由一个方程来确定一个隐函数呢?这将在第9章中给出相关结论.
它的图形为以原点为中心、半径为a的上半圆周.但不是每个隐函数都可以显化,如方程exy+x-siny=1确定的隐函数是无法显化的,因此隐函数是表达函数的一种必不可少的形式.需要注意的是:任意一个方程并不一定就能确定一个隐函数.究竟在什么条件下能够由一个方程来确定一个隐函数呢?这将在第9章中给出相关结论.
有时变量x,y之间的函数关系还可以通过参数方程
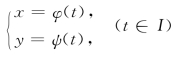
表示,这样的函数是由参数方程确定的函数,简称为参数式函数,t称为参数.
如物体作斜抛运动时,运动的路径(图1-4)对应的函数就常用参数方程
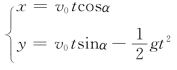
表示,其中α为初速度v0与水平方向的夹角,v0=|v0|.
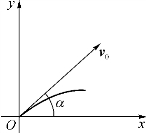
图1-4
相关文章

解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2025-09-30

函数f(z)关于闭曲线C的对数留数是指积分这里需要假定函数在C上解析.显然当C为简单正向闭曲线时,上述对数留数就是对数函数Lnf(z)的导数在C内部各个孤立奇点处留数之和.函数f(z)关于简单闭曲线C的对数留数与它在C内部的零点和极点的个数有密切的联系.即定理1 若函数f(z)在正向简单闭曲线C 上解析且没有零点,又在C的内部除有限个极点外解析,则有其中N与P分别是f(z)在C内部零点和极点的总个......
2025-09-30

虽然流线函数以及速度势函数的基本概念与计算,已经在第7章中说明,但是为了考虑本章内容的连贯性,在此以x-y平面理想流体流场为例做重点的描述及说明。流线函数φ和速度势函数Φ同时存在的判定方程式是什么?......
2025-09-29

C++语言的重载机制包含两种类型:一种是函数重载,另一种是运算符重载。对于定义的重载某一函数名的多个函数,当调用这些函数时,必须明确调用的是哪一个函数,这个过程称为重载函数的绑定。每种实现对应着一个函数体,这些函数的名字相同,但是函数的参数类型不同,这就是函数重载的概念。abs()函数重载的概念如图1.10所示。图1.10abs()函数重载分析以下程序中重载函数的情况。......
2025-09-30

若z0为函数f(z)的孤立奇点,则f(z)在z0的某个去心邻域0 <|z-z0|<R内解析.由解析函数积分的闭路变形原理,对于该邻域内任意一条围绕点z0的正向简单闭曲线C,f(z) 沿C的积分取定值,下面利用该积分来定义留数.定义1 设z0(z0 ∞)为函数f(z)的孤立奇点,C为0 <|z-z0|<R内围绕z0的任一条正向简单闭曲线,称积分为f(z)在点z0处的留数(Residue),记作Res......
2025-09-30

能较好地滤除非线性环节在正弦输入下的输出中的高次谐波,于是可以认为在闭环通道中只有基波分量在流通,此时应用描述函数法所得的分析结果才是比较准确的。描述函数类似于线性系统中的频率特性,利用描述函数的概念便可以把一个非线性元件近似地看作一个线性元件,因此又叫作谐波线性化,是线性系统频率法的推广。描述函数表达了非线性元件对基波正弦量的传递能力。......
2025-09-29

图3-1所示的是一道四宫数独原题,我们用排除法解答该题。利用A4格的数字4对一宫进行排除,得到一宫内B2格填入数字4。经过判断发现三宫这时缺数字1和2。填完一宫和三宫后,二宫和四宫也可以用相同的思路来填数。数独解题过程中往往出现在同一个情况下可以使用不同的方法和思路,而如何寻找线索并且将思路连贯起来,就是快速解题的关键所在了。......
2025-09-30
相关推荐