一般地，形如的一阶微分方程称为可分离变量的一阶微分方程.当g（y）≠0时，方程（7.2.1）可写为这样一来，变量y与x便被分离在等号的两端了.设f（x）与g（x）都连续，求解方程（7.2.1），就是要寻找函数y=y（x），将它代入方程（7.2.1）后，能使此方程成为恒等式.从而，当g（y）≠0时，就有在解微分方程时，为了突出任意常数C，常把中所含的任意常数C明确写出来.根据不定积分的第一换元法，得......
2023-10-19
高数上册：变量与数集
【摘要】：表示常量，用字母x，y，z，t，…
我们在观察某个自然现象或变化过程时，会遇到许多数量，这些数量一般可分为两类：有一类如面积、体积、长度等在该过程中保持不变的量，称之为常量；另一类在该过程中不断变化的量，称之为变量.例如在观察圆的面积大小变化时，直径与周长都是变量，而圆的周长与直径的比值（圆周率）π是一个常量；在自由落体运动中，物体的下降速度、下降时间及下降距离都是变量，而物体的质量在该过程中可以看作常量.一般地，用字母a，b，c，…表示常量，用字母x，y，z，t，…表示变量.一个量是变量还是常量，要在具体问题中作具体分析.例如就小范围地区来说，重力加速度g是不变的常量，但就广大地区来说，重力加速度g就是一个变化的量.
讨论变量间的数量关系时，需要确定变量的取值范围，单个变量的取值范围常用数集来表示.本书讨论的变量在没有特别说明的情况下都是指在实数范围内变化的量.常用的数集除了有自然数集N、正整数集N＋、整数集Z、有理数集Q、实数集R外，还常用区间和邻域来表示.
区间是用得较多的一类数集，它表示介于两个实数之间的一切数构成的实数集，在数轴上对应位于a到b之间的一条线段，设a，b∈R，且a＜b，则数集
｛x｜a＜x＜b，x∈R｝
称为开区间，记作（a，b），即
（a，b）＝｛x｜a＜x＜b，x∈R｝
数集
｛x｜a≤x≤b，x∈R｝
称为闭区间，记作［a，b］，即
［a，b］＝｛x｜a≤x≤b，x∈R｝
类似地，数集
｛x｜a＜x≤b，x∈R｝ 与 ｛x｜a≤x＜b，x∈R｝
均称为半开半闭区间，分别记作（a，b］与［a，b），即
（a，b］＝｛x｜a＜x≤b，x∈R｝，［a，b）＝｛x｜a≤x＜b，x∈R｝
其中a与b称为这些区间的端点，b－a称为这些区间的区间长度.以上四种区间均为有限区间，区间长度b－a是有限的数值.此外还有下列五种无限区间，引进记号＋∞（读作正无穷大）及－∞（读作负无穷大），则有(www.chuimin.cn)
（a，＋∞）＝｛x｜x＞a，x∈R｝，［a，＋∞）＝｛x｜x≥a，x∈R｝
（－∞，b）＝｛x｜x＜b，x∈R｝，（－∞，b］＝｛x｜x≤b，x∈R｝
（－∞，＋∞）＝R
这些区间的区间长度都为无穷大.
为了描述函数在一点邻近的某些性态，还会经常用到邻域的概念，下面引入邻域的概念.
定义1 设a，δ∈R，δ＞0，数集
称为点a的δ邻域，记作U（a，δ）.其中点a与数δ分别称为该邻域的中心与半径.
在几何上，邻域U（a，δ）表示数轴上与点a的距离小于δ的点集，因此该点集是以点a为中心，半径为δ的一个开区间（图1－1（a）），即
U（a，δ）＝（a－δ，a＋δ）
当不强调邻域的半径时，常用U（a）表示以点a为中心的任意邻域.如果将邻域U（a，δ）的中心点a去掉，得到的数集｛x｜0＜｜x－a｜＜δ｝称为以点a为中心，半径为δ的去心邻域，记作
（图1－1（b）），即
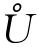（a，δ）＝（a－δ，a）∪（a，a＋δ）
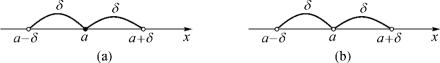
图1－1
应当指出，对于邻域的半径虽然没有明确规定其大小，但一般总是取很小的正数.
有关高等数学 上册的文章
- 详细阅读
- 详细阅读
-
高数基础：多元复合函数求导法详细阅读
在一元函数中，我们已经知道复合函数的求导公式在求导法中所起的重要作用，对于多元函数来说也是如此.下面我们来学习多元函数的复合函数的求导公式.我们先以二元函数为例，如下所述.一、全导数【知识点回顾】复合函数的求导规则：对于复合函数y=f[φ（x）]，设y=f（u），u=φ（x），其中u叫作中间变量.则复合函数求导用公式表示为：即两个可导函数复合而成的复合函数的导数等于函数对中间变量的导数乘上中间变量......
2023-11-20
-
确定冷却数和特性数的方法与注意事项详细阅读
图7-11T2—K曲线由于冷却塔内气水处于热平衡状态，即有下式成立式中符号同前，则有假设在整个塔内该式成立，则有式中T1、T2分别为进水温度和出水温度。图7-12气水比及冷却数的确定表7-1值选择范围......
2023-06-19
-
连续自然数求和：8个数之和详细阅读
★ 首先我们来计算从1开始的连续自然数的和。＋99＋100=5050★ 现在我们来计算任意连续自然数的和。方法用上面的方法，计算从1到最后一个数的和。上面两个结果相减，即可。＋1212×÷2=78再计算1＋2＋3＋……＋77×（7＋1）÷2=28两式的差为78-28=50所以8＋9＋10＋11＋12=50计算11＋12＋13＋……＋20=210-55=155计算51＋52＋53＋……＋199＋200=______计算18＋19＋20＋21＋22=______计算9＋10＋11＋12＋13＋14＋15=______计算50＋51＋……......
2023-10-27
-
标准数独技巧：九宫数独数对占位法详细阅读
我们先来看数对占位法的示意图，初步了解这种解题技巧的思路。我们将这种情况称为在五宫内形成了数字7、8的数对，该数对将D4格和F6格进行了占位。本示意图是利用数字1、3在三宫进行占位，再利用数字7排除得到确定的数字，是典型的数对占位法。如图2-21所示，G行、I行和8列都有数字1、9，利用它们对九宫进行排除，使得九宫内数字1和9只能在H7和H9两格，在九宫内形成数字1、9的数对占位。......
2023-10-29
- 详细阅读
-
高数二第二版：曲面积分计算法详细阅读
考查积分的计算，其他情形以此类推.设光滑曲面Σ：z=z（x，y）与平行于z轴的直线至多交于一点，在x Oy面上的投影区域为Dxy.由对坐标的曲面积分的定义若曲面Σ取上侧，则cosγ＞0，所以（ΔSi）xy=（Δσi）xy，否则（ΔSi）xy=-（Δσi）xy.又因为（ξi，ηi，ζi）是Σ上的一点，故ζi=z（ξi，ηi），从而有令λ→0取上式两端的极限，就得到式中右端符号的确定：若积分取曲面Σ上......
2023-10-19
相关推荐